
Предмет и цели изучения модуля № 3
3. РЕГУЛИРОВАНИЕ НАПРЯЖЕНИЯ В СЕЛЬСКИХ ЭЛЕКТРИЧЕСКИХ СЕТЯХ
Предмет и цели изучения модуля № 3
В требованиях к качеству электрической энергии, (ГОСТ 13109 - 97), указываются технически допустимые пределы отклонений значений от номинальных параметров (см. раздел 11).
Указанный ГОСТ задает допустимые отклонения напряжения на зажимах электроприемников.
Чтобы поддерживать напряжение у потребителя в допустимых ГОСТом пределах необходимо иметь в сети регулирующие напряжения средства. Изучению способов регулирования напряжения в сельских электрических сетях и посвящен этот раздел.
В результате изучения данного модуля вы будете знать:
-способы и средства повышения качества электрической энергии;
-способы регулирования реактивной мощности и повышения cosφ передачи;
-способы регулирования напряжения в электрических сетях.
Уметь:
-определять допустимую потерю напряжения в сети;
-выбирать регулировочные ответвления трансформаторов;
-выбирать конденсаторные установки для регулирования напряжения в сети.
3. РЕГУЛИРОВАНИЕ НАПРЯЖЕНИЯ В СЕЛЬСКИХ ЭЛЕКТРИЧЕСКИХ СЕТЯХ
Для улучшения режима напряжений у потребителей, увеличения допустимой потери напряжения в сети, повышения качества электроэнергии в электрических сетях применяется регулирование напряжения.
Регулирование напряжения позволяет не только улучшить эксплуатацию сети в техническом отношении, но и уменьшить стоимость ее сооружения (за счет уменьшения сечения проводов).
Если отклонения напряжения у электроприемников выходят за пределы допустимых, то в соответствии Правилами устройства электроустановок [10], для электрических сетей следует предусматривать технические мероприятия по обеспечению качества электрической энергии для выполнения требований [13].
Регулирование напряжения в электрических сетях может осуществляться следующими способами:
1. Синхронные генераторы электростанций как основные источники реактивной мощности являются также одним из основных средств регулирования напряжения. Возможности генератора как регулирующего устройства определяются его исполнением (гидро- или турбогенератор), тепловым режимом, системой возбуждения и автоматическими регуляторами возбуждения.
Регулирование возбуждения генераторов электростанций позволяет изменять напряжение в сети в относительно небольших пределах. Генератор выдает номинальную мощность при отклонениях напряжения на его выводах не более ± 5% от номинального. При больших отклонениях мощность генератора должна быть снижена. Практически этот способ регулирования может обеспечить необходимый режим напряжения для близлежащих потребителей, питающихся от шин генераторного напряжения электростанций.
2. Регулирование коэффициента трансформации трансформаторов, автотрансформаторов и линейных регуляторов. Изменение коэффициента трансформации трансформаторов, автотрансформаторов под нагрузкой производят при наличии встроенного устройства для регулирования напряжения (РПН). При этом коэффициент трансформации можно менять в широких пределах.
При помощи трансформаторов с РПН достаточно просто и экономично осуществляется встречное регулирование напряжения на шинах подстанции. Для электроснабжения сельскохозяйственных районов применяют трансформаторы типа ТМН мощностью 630-6300 кВ×А с диапазоном регулирования напряжения ±6х1,5% и ±6x1,67% номинального. Такие трансформаторы целесообразно применять на удаленных участках сети, где необходимый уровень напряжения нельзя достигнуть за счет применения других средств регулирования, и для питания потребителей, графики нагрузок которых не совпадают с графиком нагрузки распределительной сети.
Для регулирования напряжения в узловых точках распределительной сети напряжением 10-35 кВ при росте нагрузок целесообразно применять линейные регуляторы (линейные регулировочные автотрансформаторы – вольтодобавочные автотрансформаторы).
В настоящее время промышленностью выпускаются регуляторы следующих серий:
- трехфазные 400-630 кВА, РПН ±10%, число ступеней ±6, напряжением 6 - 35 кВ;
- трехфазные 1600-6300 кВА, РПН ±10%, число ступеней ±8, напряжением 6-10 кВ;
- трехфазные 16-100 МВА, РПН ±15%, напряжением 6-35 кВ;
- трехфазные 63 и 125 МВА, РПН ±15%, число ступеней ±6; напряжением 110 кВ;
С экономической точки зрения устанавливать такое регулирование напряжения целесообразно в случае компенсации ими потерь напряжения в сети не менее 4-5 %.
В сельском электроснабжении широко применяются трансформаторы с переключением без возбуждения (ПБВ), которые должны отключаться от сети для изменения коэффициента трансформации. В связи с этим изменение коэффициента трансформации производят крайне редко, например, при сезонном изменении нагрузки. Для них очень важно правильно выбрать коэффициент трансформации таким образом, чтобы режим напряжений при изменениях нагрузок был по возможности наилучшим.
В таблице 3.1 приведены добавки напряжения для трансформаторов с ПБВ, применяемых в системах сельского электроснабжения.
Таблица 3.1
Добавки напряжения трансформаторов с ПБВ с коэффициентом трансформации 10/0,4 кВ
| Регулировочное ответвление обмотки первичного напряжения | Добавка напряжения трансформатора | ||
| Порядковый номер | % | Точно | Округленно |
| 1 2 3 4 5 | -5 -2,5 0 +2,5 +5 | 0,25 2,7 5,26 7,96 10 | 0 2,5 5 7,5 10 |
3. Изменением параметров сети, которые изменяют:
а). При наличии параллельных линий, (в периоды минимума нагрузки одна из линий отключается, сопротивление цепи увеличивается, напряжение у потребителя уменьшается). Однако этот способ практически не применим для потребителей первой категории, если отключаемая линия является вторым источником питания, да и строительство второй линии только из соображения изменения напряжения нецелесообразно.
б). Компенсацией индуктивного сопротивления линии электропередачи путем последовательного включения в рассечку линии (в каждую фазу) емкостного сопротивления в виде конденсаторов. Такая компенсация называется продольной емкостной компенсацией.
На рис. 3.1 приведена схема замещения линии без компенсации и векторная диаграмма напряжений и токов линии без компенсации потерь напряжения. На рис. 3.2 приведена схема замещения и векторная диаграмма сети с продольной компенсацией. Емкостное сопротивление частично или полностью компенсирует индуктивное сопротивление линии, вследствие чего в ней уменьшаются потери напряжения, что, в конечном итоге приводит к повышению напряжения у потребителей.
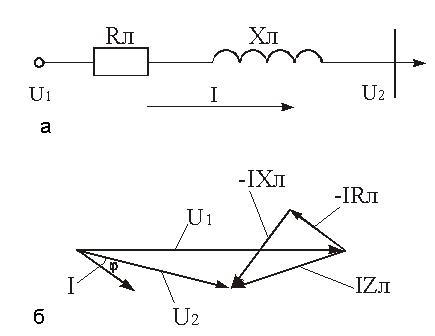 |
| Рис. 3.1. Схема замещения (а) и векторная диаграмма напряжений (б) сети без компенсации потерь напряжения |
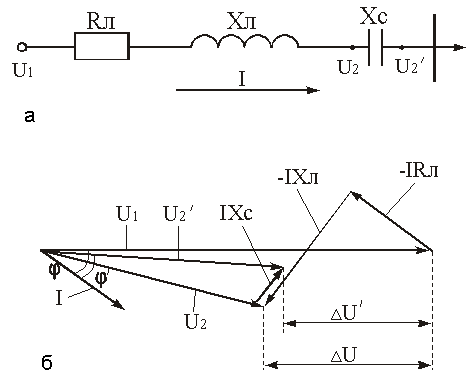 |
| Рис. 3.2. Схема замещения (а) и векторная диаграмма напряжений (б) сети с продольной компенсацией потерь напряжения |
Регулирование напряжения таким способом имеет ряд преимуществ перед другими способами:
- продольная емкостная компенсация имеет сравнительно простую конструкцию;
- компенсирующий эффект установки зависит от тока нагрузки (размер компенсации потери напряжения с ростом нагрузки возрастает и, наоборот, снижается при ее уменьшении).
Продольная и поперечная составляющие падения напряжения без компенсации мощности соответственно равны:
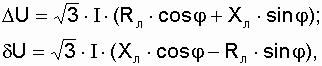 | (3.1) |
где I – полный ток нагрузки, А;
Rл, Хл – соответственно активное и индуктивное сопротивление линии, Ом.
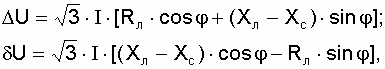 | (3.2) |
где Хс – емкостное сопротивление конденсаторов, включенных последовательно в линию.
В практических расчетах обычно поперечной составляющей падения напряжения из-за ее незначительности пренебрегают. Поэтому из приведенных формул имеем, что при продольной компенсации
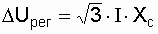 , , | (3.3) |
где I – ток нагрузки; Хс – сопротивление конденсатора.
Мощность конденсаторов определяется по формуле:
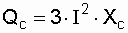 , , | (3.4) |
где I – наибольший ток линии.
В практических расчетах мощность конденсаторов определяют исходя из желаемого уровня напряжения в сети при известном сечении провода по следующей формуле:
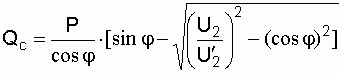 , , | (3.5) |
где P – активная мощность, проходящая через конденсатор, Вт;
U2 – напряжение на входных (со стороны питания) зажимах конденсатора, В;
U¢2 – напряжение на выходных (со стороны потребителя) зажимах конденсатора, В;
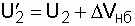 ,
,
где DVнб – желаемая надбавка напряжения, достигаемая включением конденсаторов.
При выборе установок для продольной компенсации следует помнить, что нежелательно параллельно включать конденсаторы в одну фазу, так как при этом уменьшается их общая емкость и при несовпадении характеристик конденсаторов распределение тока между ветвями будет неравномерным. В нормальном режиме работы сети напряжение на зажимах конденсаторов пропорционально протекающему по ним току и составляет 5 - 10% номинального напряжения сети. Это дает возможность устанавливать конденсаторы с номинальным напряжением, много меньшим номинального напряжения сети (см. пример 3.1). Однако при коротком замыкании за конденсатором напряжение на их зажимах может достигнуть такого значения, при котором конденсаторы, если не принять специальных мер защиты, будут пробиты. Конденсаторы обладают большой перегрузочной способностью по напряжению, значение которой зависит от продолжительности протекания тока короткого замыкания. Значение допустимой кратковременной перегрузки по напряжению в расчетах принимают равным 3,5. Провер ка устройств продольной компенсации на перегрузочную способность заключается в определении тока короткого замыкания и расчетной кратности перенапряжения, которую сравнивают с допустимой. Наиболее приемлемыми средствами защиты от перенапряжений являются разрядники с вращающейся дугой и нелинейные ограничители перенапряжений (см. раздел 5).
На рис. 3.3 приведена схема установки продольной компенсации с комплектами разрядных сопротивлений R1 и R2. На комплект R1 конденсаторы разряжаются при срабатывании разрядников, а на комплект R2 – при шунтировании УПК разъединителем.
 |
| Рис. 3.3. Схема установки устройства продольной компенсации |
4. Изменением величины реактивной мощности, протекающей в сети.
Основными потребителями реактивной мощности в сельскохозяйственном производстве являются асинхронные двигатели. Часть реактивной мощности теряется в обмотках трансформаторов и в проводах линии электропередачи. Передача реактивной мощности по сети для этих потребителей вызывает дополнительные потери напряжения и электроэнергии.
 |
| Рис. 3.4. Схема замещения (а) и векторная диаграмма напряжений (б) сети с поперечной компенсацией потерь напряжения |
Для разгрузки сети от реактивной мощности целесообразно эту мощность или ее часть генерировать на месте потребления. Источниками реактивной мощности являются синхронные компенсаторы, статические конденсаторы, устанавливаемые на месте потребления и подключаемые параллельно нагрузке (поперечная компенсация). Векторная диаграмма напряжений с учетом поперечной компенсации приведена на рис. 3.4.
В сельских сетях наиболее широко используются статические конденсаторы на напряжении до 1000 В и 10 кВ. Конденсаторы в этом случае являются потребителями опережающей (емкостной) мощности, или, что, то же самое, источниками реактивной мощности.
Потеря напряжения при поперечной компенсации определяется:
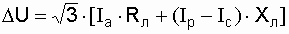 | (3.6) |
Значит при параллельном включении конденсаторов
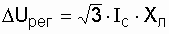 , , | (3.7) |
где Ic – емкостной ток линии;
Хл – индуктивное сопротивление линии.
Мощность конденсаторов для компенсации при параллельном включении определяется
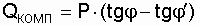 , , | (3.8) |
где P – активная мощность потребителей, кВт;
P·tgφ – реактивная мощность потребителей без компенсации;
P·tgφ¢ – реактивная мощность, передаваемая по линии при наличии компенсации.
Емкость конденсаторов равна
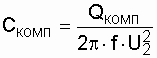 , , | (3.9) |
где f – частота тока.
Выбрать продольную компенсацию для сети напряжением 10 кВ с нагрузками в кВт и квар и длинами в км, указанными на рисунке 3.5. Напряжение на шинах питающей подстанции составляет 10350 В. Допустимая потеря напряжения в сети составляет 6,5%. Параметры участков сети приведены в таблице 3.1.
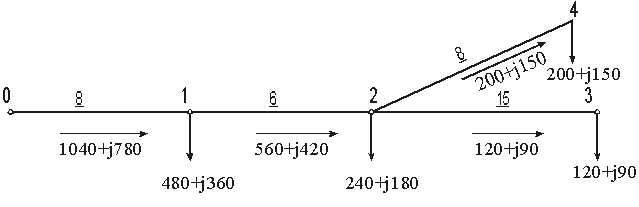 |
| Рис. 3.5. Схема сети к заданию 3.1 |
Таблица 3.1
| № участка | Марка провода | r0, Ом/км | х0, Ом/км | L,км |
| 0-1 | АС-70 | 0,42 | 0,392 | 8 |
| 1-2 | АС-70 | 0,42 | 0,392 | 6 |
| 2-3 | АС-25 | 1,146 | 0,415 | 15 |
| 2-4 | АС-35 | 0,773 | 0,403 | 8 |
Решение: Определим допустимую потерю напряжения в сети по условию задачи
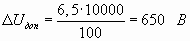 .
.
Фактические потери напряжения по участкам сети при заданных параметрах и при заданных нагрузках
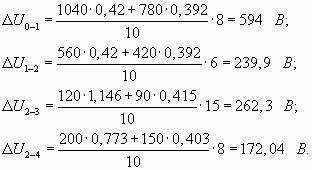
Полная потеря напряжения до потребителей:
ΔU0-1=594;
ΔU0-2=594+ 239,9=833,9 В;
ΔU0-3=594+ 239,9 + 262,3=1096,2 В;
ΔU0-4=594 + 239,9 + 122,4=956,3.
Как показали расчеты потери напряжения до потребителей 2, 3, 4 значительно превышает допустимые 650 В.
Место установки продольной компенсации определим исходя из следующих рассуждений: так как у нагрузки в узле 1 потери напряжения находятся в допустимых пределах (594,3< 650), а у нагрузки в узле 2 потеря напряжения превышает допустимую (833,9> 650), то продольную компенсацию целесообразно установить в конце участка 1-2.
Тогда напряжение на входе конденсатора будет
U2=10350 – 833,9=9516,1 В.
Желаемое напряжение на выходе конденсатора определим с учетом допустимой потери напряжения и с учетом необходимости компенсации потерь до нагрузки, имеющей наибольшие потери напряжения (узел 3).
U¢ 2=10350 – 650 + 262,3=9962,3 В.
Определим расчетную мощность конденсаторов по формуле (3.5)
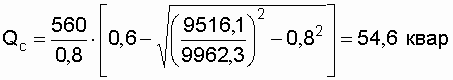 .
.
Выберем тип и число конденсаторов. При выборе типа конденсаторов определяющими параметрами являются максимальный ток, протекающий по линии и расчетное сопротивление конденсаторов.
В нашем случае через конденсатор течет ток участка 1-2.
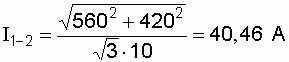 .
.
Расчетное емкостное сопротивление фазы в соответствии с формулой (3.4)
 .
.
Сопротивление выбранных конденсаторов должно быть как можно ближе к расчетному сопротивлению, но не менее него.
Максимально возможное напряжение на конденсаторе составляет:
U¢ 2 – U2=9962,3 – 9516,1=445,9 В, поэтому выбираем конденсаторы продольной установки с номинальным напряжением 1 кВ КПМ-30 с мощностью одной фазы 30 квар. Номинальный ток этого конденсатора Iном=50 А. Сопротивление
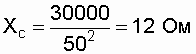 .
.
Всего устанавливаем три конденсатора (по одному на фазу).
Определим действительную надбавку напряжения, получаемую при помощи выбранных конденсаторов, для этого проведем поверочный расчет сети. Схема сети с продольной компенсацией приведена на рисунке 3.6.
Конденсаторная установка генерирует в сеть реактивную мощность в зависимости от расчетного значения тока, протекающего по ней и сопротивления фазы конденсатора.
Qс=3× 40,462× 12=58,9 квар.
Эта опережающая мощность уменьшает реактивную мощность, протекающую по участкам 0-1 и 1-2. Новое распределение мощностей приведено на рисунке 3.6.
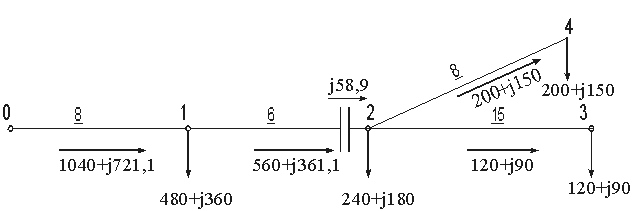 |
| Рис. 3.6. Схема сети к заданию 3.1 после установки продольной компенсации |
Определим потери напряжения по участкам после компенсации.
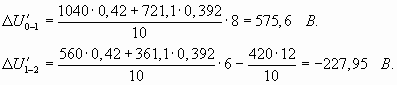
Суммарная потеря напряжения до узлов 3 и 4 составит
ΔU0-3=575,6 – 227,95 + 262,3=609,95 В;
ΔU0-4=575,6 – 227,95 + 172,04=519,69 В,
что меньше допустимой по условию задачи потери напряжения.
Место продольной компенсации выбрано правильно, так как обеспечивает заданную допустимую потерю напряжения.
Выбрать конденсаторную батарею для компенсации коэффициента мощности свинарника на 8000 тыс. голов до значения cosφ'=0,925 и проверить фактический коэффициент мощности с выбранной батареей, если при отсутствии компенсирующих устройств дневной максимум активной нагрузки Р=185 кВт, а реактивной 165 квар.
Решение: Мощность конденсаторной батарей рассчитаем по формуле (3.8).
Определим tgφ до установки батареи tgφ=165/185=0,89;
cosφ'=0,925 соответствует tgφ'=0,41.
Тогда Qкомп=185 · (0,89 – 0,41)=88,8 квар.
Для установки выбираем три конденсатора мощностью по 35 квар каждый. Батарею соединяем по схеме треугольника, подключаем параллельно шинам 0,4 кВ.
Определим фактический коэффициент мощности в сети при номинальном напряжении на шинах. При номинальном напряжении на шинах батарея конденсаторов будет генерировать в сеть мощность равную номинальной трехфазной мощности, т.е. 105 квар. Тогда полная мощность, передаваемая по сети после компенсации составит:
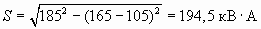 ,
,
а фактический коэффициент мощности cosφфакт=185/194,5=0,95.
Какой величины будет cosφ после компенсации реактивной мощности с помощью батареи конденсаторов Qконд=30 квар, установленной на вводе в кормоцех фермы КРС на 800 голов с расчетной мощностью 50 кВт и коэффициентом мощности до компенсации cosφ=0,74?
Решение: Определим полную и реактивную мощность, потребляемую кормоцехом.
S=50/0,74=67,57 кВ·А;
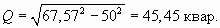
После компенсации реактивная мощность передаваемая по сети составит Qпер=67,57 – 30=37,27 квар.
Полная мощность передаваемая по сети после компенсации:
Qпосле комп=45,45 – 30=15,45 квар.
Полная мощность:
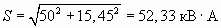 .
.
Тогда коэффициент мощности после компенсации составит:
cosφпосле комп.=50/52,33=0,96.
Регулирование напряжения в сельских электрических сетях конденсаторными установками
Цель работы: изучение способов регулирования напряжения в сельских электрических сетях, исследование регулирования напряжения использованием конденсаторов, определение оптимальных емкостей статических конденсаторов при продольной и поперечной компенсации реактивной мощности для улучшения качества напряжения и cosφ.
Указания к выполнению работы
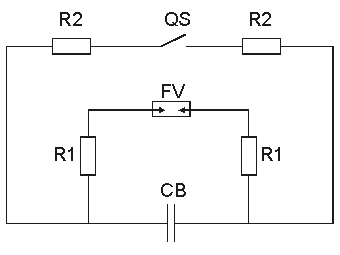
Компенсирующие устройства изучают на модели одной фазы линии, принципиальная схема которой показана на рис. 3.7. Номинальное напряжение модели 100 В. Схема замещения модели линии приведена на рис. 3.8.
Питание на модель подается выключателем QF, напряжение источника питания регулируется лабораторным автотрансформатором.
Сопротивление участков сети имитируется активными и реактивными сопротивлениями Rл Xл. Нагрузки сети Zн1 и Zн2 на модели имитируется постоянными сопротивлениями, нагрузка Zн3 переменная, и ее значение задается преподавателем для каждой бригады студентов.
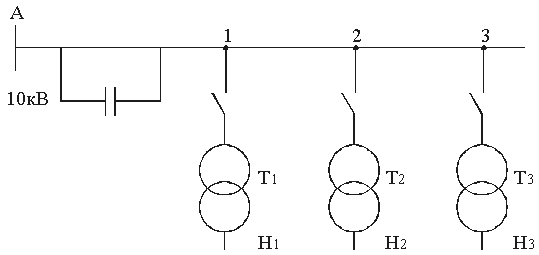 |
| Рис. 3.7. Принципиальная схема сети 10 кВ |
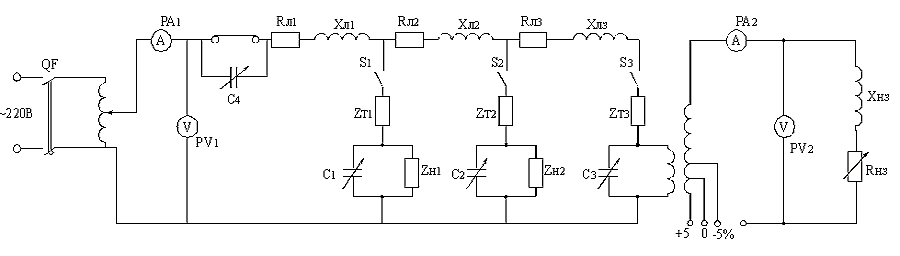 |
| Рис. 3.8. Схема замещения сети 10 кВ |
Трансформатор Т3 у нагрузки Н3 позволяет изменять напряжение на стороне 0,4 кВ изменением коэффициента трансформации ответвлениями +5%; 0%; -5%.
Ток нагрузки Н3 и напряжение на низкой стороне трансформатора Т3, а также напряжение источника питания измеряют амперметром рА2 и вольтметром рV2.
Ток, напряжение и мощность на ответвлениях к нагрузкам измеряют также при помощи переносных приборов и специальных кнопок включения.
Для поперечной компенсации реактивной мощности нагрузок Zн1 ,Zн2, Zн3 предусмотрены емкости, выключатели которых смонтированы на модели.
Необходимо помнить: чтобы контакты емкостей не подгорали, их следует включать и отключать при снятии напряжения.
При включении продольной компенсации нужно переключить тумблер в положение (вкл), включенного последовательно в линию конденсатора.
Экспериментальную часть работы следует начинать с установки значения напряжения на шинах источника питания, которое задается преподавателем.
Так как на модели невозможно работать с действительными (реальными) значениями напряжения и тока, надо пользоваться масштабами замеряемых величин, выбирая их исходя из возможностей модели и удобства замеров. Масштабы определяют по следующим формулам:
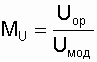 – масштаб напряжения;
– масштаб напряжения;
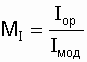 – масштаб тока;
– масштаб тока;
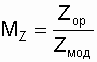 – масштаб сопротивления;
– масштаб сопротивления;
Mр=Мs=MI·MU – масштаб мощности.
Токи, напряжения и мощности, замеренные на модели, приводят к значениям оригинала по формулам:
Iор=Iмод·МI;
Uор=Uмод·Мu;
Pор=Pмод·Mр.
В каждом из опытов напряжение и ток необходимо замерять при напряжении на шинах источника питания, равном 100 В или по заданию преподавателя на 5-10% выше номинального напряжения линии (т.е. 105 В или 110 В).
Таблица 3.2.
Результаты измерений при поперечной компенсации
| № цепи | С, мкФ | U, В | I, A | P, Вт | S, В·А | cosφ | Qрасч, вар | Срасч, мкФ |
| 1 | – | |||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 2 | – | |||||||
| 2 | ||||||||
| 4 | ||||||||
| 3 | – | |||||||
| 0,1 | ||||||||
| 0,5 |
Таблица 3.3
Результаты измерений при продольной компенсации
| Uвх | Uвых | I1 | P2 | P3 | P4 | Qрасч | Срасч |
| В | В | А | Вт | Вт | Вт | вар | мкФ |
Таблица 3.4
Результаты измерений поперечной компенсации в точке 3 с переключением ПБВ
| ПБВ | С, мкФ | U4, В | I4, А | P4, Вт | S4, В·А | cosφ | Qрасч, квар | Срасч, мкФ | U3, В |
I3, А |
| 0 | ||||||||||
| -5 | ||||||||||
| +5 | ||||||||||
Таблица 3.5
Действительные значения величин в линии 10 кВ
| Режим работы линии | Контрольные точки | U, кВ | I, А | P, кВт | S, кВ×А | сosj | C, мкФ |
| Без компенсации | А А΄ 1 2 3 | ||||||
| С поперечной компенсацией | А А΄ 1 2 3 | ||||||
| С продольной компенсацией | А А΄ 1 2 3 |
Оформление отчета
Отчет должен содержать:
Контрольные вопросы
1. Назовите возможные способы регулирования напряжения в сельских электрических сетях.
2. Что такое продольная и емкостная компенсация потерь напряжения?
3. Постройте векторные диаграммы напряжений сети без компенсации потерь напряжения и с продольной и поперечной компенсацией.
4. Влияние отклонения напряжения на работу потребителей электроэнергии.
5. Назовите основные показатели качества электроэнергии.
6. Как влияет величина сosφ на потери энергии в сети?