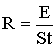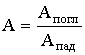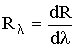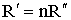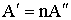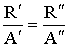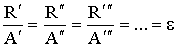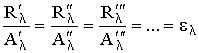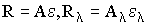Энергетическая светимость имеет размерность [Дж/(м2·с)].
А - безразмерная величина. Величины R и А зависят от природы тела и от температуры. Опыт показывает, что энергия, испускаемая (поглощаемая) телом, различается для различных длин волн. В связи с этим вводится понятие спектральной испускательной (поглощательной) способности.
Поглощательная способность всех реальных тел меньше единицы. Например, для видимой части спектра А(Al) = 0,1; A(Cu) = 0,5; A(H2O) = 0,67. Воображаемое тело, поглощающее при любой температуре всю падающую на него лучистую энергию, называется абсолютно черным телом. Поглощательная способность такого тела для всех длин волн одинакова и равна единице:
Для видимой части спектра телом, близким по своим свойствам к абсолютно черному, является сажа (А = 0.95). моделью черного тела является сферическая полость с малым отверстием, внутренняя поверхность которой зачернена. Луч, попавший в отверстие, претерпевает многократные отражения стенками полости и практически не выходит обратно, поскольку при каждом отражении часть его энергии поглощается. Абсолютно черное тело, поглощая падающую на него лучистую энергию, вместе с тем само излучает. Поэтому при низкой температуре полости отверстие в ней кажется черным; если же полость нагрета до высокой температуры, то отверстие представляется ярко светящимся. Примерами, близкими к абсолютно черному телу, могут служить зрачок глаза и смотровое отверстие мартеновской печи. Испускательная и поглощательная способности тела связаны между собой. Рассмотрим изолированную систему из двух тел, имеющих различную температуру и обменивающихся энергией посредством лучеиспускания и лучепоглощения. Через некоторое время в системе установится тепловое равновесие. Пусть значения испускательной и поглощательной способностей тела при двух температурах лучистого равновесия равны: R', R'' и A', A''. Предположим, что первое тело испускает в единицу времени с единицы площади в n раз больше энергии, чем второе:
Однако тогда первое тело должно и поглощать в n раз больше энергии, чем второе:
поскольку иначе первое тело начнет охлаждаться по сравнению со вторым, что противоречит условию теплового равновесия. Из (4.2.6) и (4.2.7) следует, что:
Если изолированная система состоит из многих тел с различными испускательными и поглощательными способностями, и одно из них является абсолютно черным, то аналогично можно придти к выводу:
где ε - испускательная способность абсолютно черного тела, поскольку его поглощательная способность А = 1. Для всех тел при данной температуре отношение испускательной способности к поглощательной способности есть постоянная величина, равная испускательной способности абсолютно черного тела при той же температуре (закон Кирхгофа). Закон Кирхгофа справедлив и для спектральных испускательной и поглощательной способностей тел:
Следствия закона Кирхгофа:
Соотношения (4.2.11) позволяют определять испускательную способность любого тела, если известны его поглощательная способность А и испускательная способность абсолютно черного тела e. Значения А и ε определяют опытным путем. Изменяя поглощательную способность поверхности земли, можно в значительных пределах регулировать температуру теплового равновесия верхнего слоя почвы. Это делают в агрономии с помощью мульчирования. Например, для увеличения поглощательной способности почвы применяют темную мульчу (торфяной и угольный порошок), для уменьшения - светлую (молотый мел). 4.2.2. Законы излучения
|
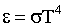 | (4.2.12) |
где σ = 5,67·10-8 Вт·м-2·К-4 - постоянная Стефана-Больцмана.
Спектральная плотность энергетической светимости абсолютно черного тела имеет максимум, который смещается в зависимости от абсолютной температуры этого тела. На Рис. 4.2.1 показано распределение энергии и смещение максимума при различных температурах в спектре излучения угля близком к абсолютно черному телу.
Рис. 4.2.1. Спектральная плотность излучения угля
Характер этого смещения выражается законом Вина - длина волны, соответствующая максимуму излучения абсолютно черного тела, обратно пропорциональна его абсолютной температуре:
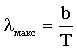 | (4.2.13) |
где b = 2,9·10-3 м·К - постоянная Вина.
Из Рис. 4.2.1 следует, что с повышением температуры испускательная способность возрастает (увеличивается площадь под кривой), а длина волны, соответствующая максимуму излучения, уменьшается.
Наглядным примером, подтверждающим изменение длины волны максимума излучения, является изменение цвета свечения нагреваемого металла. Сначала металл остается темным (максимум лежит в ИК области спектра), затем при достаточно высокой температуре появляется красное свечение металла ("красное каление"), потом оранжевое, желтое и, наконец, голубовато-белое свечение ("белое каление"). Конечно, металл не является абсолютно черным телом, но некоторые черты последнего сохраняются.
При температуре 6000 К максимум излучения приходится на видимый свет (λмакс ≈ 0,5 мкм). Отсюда следует, что наиболее выгодный в световом отношении источник света должен иметь такую температуру, при которой световой КПД (отношение энергии излучения, приходящейся на видимую часть спектра, ко всей энергии излучения) оказывается около 15%, поскольку большая часть энергии излучения приходится на ИК лучи. У современных осветительных ламп температура нити накала равна приблизительно 3000 К, что соответствует световому КПД примерно 3%.
На законе Вина основана оптическая пирометрия. Так, максимум излучения Солнца приходится на видимый свет (λмакс ≈ 0,47 мкм). Поэтому, согласно закону Вина, имеем:
Законы Стефана-Больцмана и Вина являются частными законами излучения абсолютно черного тела, они не дают полной картины распределения энергии по длинам волн при различных температурах.
4.2.3. Световые кванты.
Формула Планка
Макс Планк высказал революционную гипотезу, согласно которой электромагнитная энергия может излучаться только определенными порциями - квантами ε - энергии. Поэтому излучение любого тела производится с энергией, кратной минимальному значению nε (n = 1, 2, 3, ...). Квант энергии электромагнитного излучения пропорционален частоте (обратно пропорционален длине волны):
 | (4.2.14) |
где с - скорость света в вакууме, h = 6,625·10-34 Дж·с - постоянная Планка.
По формуле (4.2.14) можно вычислить квант энергии для излучения с любой длиной волны.
Процесс поглощения также, как и процесс излучения электромагнитной энергии, имеем прерывистый (квантовый) характер. Особенно заметны квантовые особенности поглощения и излучения для коротких длин волн, порождаемых атомами и молекулами. Поэтому законы классической физики, полученные из наблюдений за макрообъектами, не вполне пригодны для описания процессов, происходящих на уровне атомов и молекул или еще более глубоких степенях изучения материи.
На основе представлений о квантовом характере теплового излучения Планк получил такое выражение для спектральной излучательной способности абсолютно черного тела:
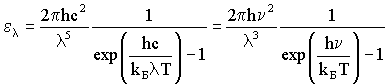 | (4.2.15) |
Формула Планка находится в полном соответствии с опытными данными. Из нее могут быть получены законы Стефана-Больцмана и Вина.
4.2.4. Фотоэлектрический эффект.
Закон Эйнштейна
Помимо волновых свойств, свет обладает некоторыми свойствами, которые позволяют сказать, что световой поток - это поток особых частиц (фотонов), обладающих определенной энергией и импульсом. Одним из доказательств этого были опыты по изучению внешнего фотоэлектрического эффекта. Эти опыты служат также доказательством гипотезы Планка о квантах.
Фотоэффектом называется освобождение (полное или частичное) электронов от связей с атомами и молекулами вещества под воздействием света. Внешний фотоэффект - это явление вырывания электронов из твердых и жидких веществ под действием света, при этом электроны выходят за пределы вещества. Если электроны остаются внутри вещества, но освобождаются от связи с конкретным атомом, то такой фотоэффект называют внутренним. Внешний фотоэффект наблюдается у металлов (Рис. 4.2.2).
Рис. 4.2.2. Схема наблюдения внешнего фотоэффекта
Отрицательный полюс батареи присоединен к металлическому катоду (например, из цинка), который освещается через прозрачное окно. Как только на катод падает свет, вырываемые из него фотоэлектроны начинают двигаться к аноду, и в цепи возникает ток, регистрируемый гальванометром.
Было установлено, что фотоэффект может быть объяснен на основе квантовой теории света. По этой теории, световой поток определяется некоторым числом световых квантов, падающих на поверхность металла в единицу времени. Каждый фотон может взаимодействовать только с одним электроном. Поэтому максимальное число фотоэлектронов должно быть пропорционально световому потоку. Полностью фотоэффект можно описать с помощью закона Эйнштейна:
 | (4.2.16) |
где А - работа выхода электрона из металла или жидкости, m - масса и v - скорость вырванных электронов (фотоэлектронов).
Из уравнения Эйнштейна следует, что энергия одного светового кванта затрачивается на вырывание одного электрона и придания ему кинетической энергии. Поскольку А - величина для данного вещества постоянная, скорости фотоэлектронов оказываются зависящими только от частоты падающего света. Например, для платины А = 5,29 эВ, для цинка А = 4,19 эВ, для цезия А = 1,89 эВ. Внешний фотоэффект возможен, когда выполняется неравенство:
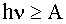 | (4.2.17) |
В случае равенства энергии фотона работе выхода получаем:
 | (4.2.18) |
Частота (4.2.18) соответствует красной границе фотоэффекта, поскольку это минимальная частота, еще вызывающая фотоэффект. Ей соответствует длина волны света, близкая к длинным волнам (красной части спектра).
Применение внешнего фотоэффекта позволило создать вакуумный фотоэлемент. Материалом катода является соединения сурьмы и цезия или цезия и кислорода, обладающие высокой фоточувствительностью.
Внутренний фотоэффект наблюдается в полупроводниках и в некоторых диэлектриках. Фотоэлементы, основанные на внутреннем фотоэффекте, называются фотосопротивлениями, поскольку при освещении такого прибора его электрическое сопротивление резко уменьшается.
Фотоэффект в полупроводниках применяют также для создания солнечных батарей.
4.2.5 Взаимодействие света с веществом.
Поглощение света. Закон Бугера.
Закон Бугера-Ламберта-Бера
Рис. 4.2.3 Схема к выводу закона поглощения света (черными точками обозначены атомы, в которых фотоны были захвачены электронами)
При прохождении света через вещество часть фотонов захватывается атомами вещества и световой поток ослабляется. Захват фотона может происходить вследствие фотоэффекта или вследствие возбуждения атома, при котором фотон переводит оптические электроны атома на энергетические уровни. Чем больше атомов и молекул встретится на пути светового потока, тем больше вероятность захвата фотона и тем больше поглощение света.
Поглощением света называют ослабление интенсивности света при прохождении через любое вещество вследствие превращения световой энергии в другие виды энергии.
Интенсивностью света называется отношение энергии, переносимой светом через площадь, перпендикулярную световому лучу, к продолжительности времени переноса и к размеру площади.
Установим закон поглощения света веществом. Направим на плоскую поверхность параллельный пучок света (Рис 4.2.3). Пусть I0 –интенсивность падающего света на вещество толщиной l. На расстоянии x от поверхности мысленно выделим бесконечно тонкий слой вещества dx. Интенсивность света dl, поглощенного этим слоем, пропорциональна интенсивности падающего на него света I и количеству атомов, находящихся в этом слое, которое пропорционально толщине слоя dx: dI = -χIdx. Знак минус означает, что интенсивность света уменьшается. Коэффициент пропорциональности χ характеризует поглощение света в слое единичной толщины и называется коэффициентом поглощения. Интегрируя последнее равенство и подставляя соответствующие пределы, получим
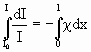 . | (4.2.19) |
После интегрирования получим: lnI – lnI0 = χ l. Отсюда
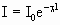 . | (4.2.20) |
Из этой формулы видно, что коэффициент поглощения есть величина обратная толщине такого слоя вещества, который ослабляет интенсивность света в е раз. Это уравнение носит название закона Бугера.
Для растворов показатель поглощения пропорционален концентрации вещества С, то есть χ = ε С, где ε - показатель поглощения света на единицу концентрации вещества или молярный коэффициент поглощения. Подставляя это значение в закон Бугера, получим закон Бугера - Ламберта - Бера
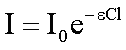 | (4.2.21) |
Если перейти от натурального логарифма к десятичному, то получим закон тот же закон Бугера – Бера - Ламберта
 . | (4.2.22) |
Прологарифмируем:
 , | (4.2.23) |
где D называется оптической плотностью вещества, а ε’ отличается от ε только численным значением, связанным с переходом от натурального логарифма к десятичному. Оптическая плотность раствора пропорциональна концентрации вещества в растворе и толщине слоя, в котором происходит поглощение. Оптическая плотность характеризует поглощающую способность вещества. Если свет поглощается сложной системой (например, биологической тканью), то общая величина оптической плотности такой системы равен сумме оптических плотностей составляющих ее компонентов, что объясняется независимостью акта поглощения фотонов одним компонентом от свойств другого компонента.
Отношение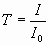 
называется коэффициентом пропускания. Очевидно, что
| D = lg(1/T). | (4.2.24) |
Оптическая плотность, равная 1, соответствует пропусканию 0,1 или 10%. Если D = 2, то Т = 1% и т.д.
Коэффициент поглощения и оптическая плотность зависят от длины волны.
4.2.6 Спектры поглощения
Зависимость оптической плотности от длины волны называют спектром поглощения. График этой зависимости представляет собой кривую с максимумами в определенных интервалах длин волн, в которых происходит сильное поглощение света данным веществом. Эти интервалы называют полосами поглощения. У прозрачных тел (вода, стекло) полосы поглощения находятся в инфракрасной или в ультрафиолетовой части спектра. У белков максимум поглощения соответствует 250 нм, у нуклеиновых кислот – 60 нм и т.д. Зеленое тело поглощает свет во всех участках видимого спектра, кроме зеленого.
Наибольшей простотой отличаются спектры одноатомных разреженных газов или паров металлов. Они состоят из отдельных узких линий и называются линейчатыми. Это обусловлено тем, что отдельный атом может поглотить квант света только при условии, что его энергия в точности равна разности энергий между определенными электронными уровнями.
Спектры газов, состоящих из многоатомных молекул (молекулярные спектры), значительно сложнее атомных, что обусловлено большим разнообразием движений и, следовательно, энергетических переходов в молекуле. Это приводит к тому, что спектры поглощения молекул состоят из широких полос, разделенных широкими же промежутками. Такие спектры называют полосатыми.
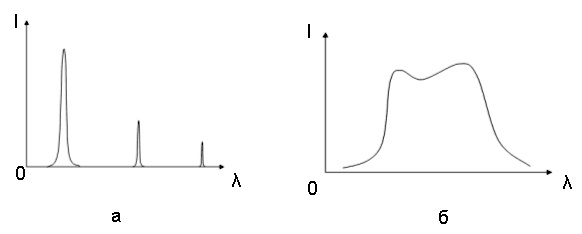
Рис.4.2.4. Спектры линейчатые(а) и непрерывные (б).
4.2.7 Физические явления, сопровождающие поглощение света веществом
В начале любого процесса взаимодействия света с веществом находится акт поглощения фотона электроном. Если энергия фотона больше работы выхода электрона из атома, то происходит фотоэффект, который приводит к ионизации атомов и разрывам химических связей между атомами в молекулах. Фотоны с меньшей энергией переводят атомные электроны из основного состояния на более высокие энергетические уровни, что приводит к возбуждению атомов и молекул. Однако атомы и молекулы, как правило, не могут долго находиться в возбужденном состоянии и передают избыточную энергию окружающей среде в одном из следующих процессов.
1. Безызлучательный переход в основное состояние, при котором энергия возбуждения передается окружающим молекулам и в конечном счете переходит в теплоту. Точно так же переходит в теплоту и энергия электронов, переведенных в основное состояние в результате фотоэффекта, если эти электроны остаются внутри облучаемого тела.
2. Фотохимическая реакция, то есть реакция, обусловленная возбуждением молекулы фотоном или ионизацией молекулы при вылете из нее фотоэлектрона.
3. Люминесценция-переход электронов в основное состояние в молекуле с испусканием одного или последовательно нескольких фотонов.
Рассмотрим последний процесс.
4.2.8 Люминесценция
Квантовый механизм люминесценции
Излучение фотона происходит при переходе атомного электрона с более высокого на низшие энергетические уровни. Перевести атомы в возбужденное состояние, при котором оптические электроны находятся на более высоких энергетических уровнях, можно, либо нагревая тело до высокой температуры, либо облучением света или рентгеновскими лучами или бомбардировкой элементарными частицами. Если электроны задерживаются на энергетических уровнях и испускание фотона происходит через время, значительно превышающий период излучаемых световых волн (~10-14 с), то явление излучения света носит название люминесценция.
Люминесценцией называют излучение, представляющее собой избыток над тепловым излучением тела при данной температуре при условии, если это излучение обладает длительностью послесвечения от 10-10 с и больше. Временем послесвечения считают промежуток времени между моментом перевода атома или молекулы в возбужденное состояние и моментом испускания ими фотона.
Различают несколько типов люминесценции.
Фотолюминесценция возникает при освещении видимым или ультрафиолетовым светом. Наблюдается во всех агрегатных состояниях вещества.
Хемилюминесценция – свечение, возникающее в результате химических реакций. Частным случаем хемилюминесценции является биохемилюминесценция – свечение в живых организмах в результате происходящих в них химических реакций.
Катодолюминесценция – свечение, вызванное действием катодных лучей, т.е. потоком электронов, ускоренных электрическим полем.
Рентгенолюминесценция и радиолюминесценция, вызываемое рентгеновскими лучами и ионизирующими излучениями. По длительности свечения люминесценция подразделяется на флуоресценцию (кратковременное свечение) и фосфоресценция (длительное послесвечение).
4.2.9
Правило СтоксаНачальным актом любой люминесценции является возбуждение фотоном с энергией hν атома или молекулы. В простейшем случае, когда вещество состоит из практически невзаимодействующих атомов , возбужденный атом возвращается в основное состояние и излучает фотон с той же энергией. Это явление происходит с длительностью послесвечения порядка 10 нс, и его называют резонансной флуоресценцией (резонансной потому, что частоты падающего и испускаемого света одинаковые). Схема этого процесса показана на рис.4.2.5а
На энергию электрона в молекуле оказывают влияние вращательное движение молекулы и колебания атомов в молекуле. В связи с этим энергетические уровни молекул состоят из полос, в каждой из которых имеется много близко расположенных друг от друга подуровней. Возбужденный электрон переходит сначала на низший возбужденный подуровень, при этом фотоны не излучаются, а энергия переходит безызлучательно в тепловую энергию кристаллической решетки, затем электрон переходит на основное состояние (рис.4.2.5б). В этой схеме излучается фотон с энергией, меньшей энергии падающего фотона:
hνлюм = hνпогл-Етепл.
Поэтому длина волны света, испускаемого при люминесценции, больше длины волны падающего света. Это положение называется правилом Стокса.
При антистоксовой люминесценции длина волны испускаемого света короче длины волны поглощенного света. Причина этого в том, что электроны, переходя на возбужденные уровни, могут получить дополнительную энергию от колебательного движения молекулы. Возможны также переходы на один из уровней, имеющих энергию, меньшую, чем основной уровень (рис.4.2.5в).
Поскольку электроны совершают переходы между полосами, состоящими из многих подуровней, то свет, испускаемый при люминесценции, будет иметь не одну частоту, а более сложный спектр. Поэтому правило Стокса имеет более общую формулировку: максимум спектра люминесценции сдвинут по отношению к максимуму спектра поглощения в сторону более длинных волн.
4.2.10 Люминесцентный анализ
Люминесцентным анализом называют метод исследования различных объектов под действием ультрафиолетового облучения, вызывающего люминесценцию этих объектов. При люминесцентном анализе наблюдают или собственное свечение исследуемых тел, или свечение люминифоров, которые вводят в эти тела. Такой анализ позволяет исследовать вещество при чрезвычайно малых количествах люминесцирующих примесей. Например, содержание флуоросцеина, святящегося под действием УФ облучения зеленоватым светом, можно обнаружить, когда в 1 мл воды находится 10-10 г этого вещества.
Люминесцентный анализ применяют в самых различных областях науки и практики. Так, в криминалистике облучение УФ позволяет обнаружить невидимые следы крови, причем свечение крови человека отличается от свечения крови животных и птиц.
Широкое применение нашел люминесцентный анализ в ветеринарно-санитарной экспертизе, которую проводят для контроля продуктов питания на мясомолочных контрольных станциях, в пищевых ветеринарных лабораториях и на колхозных рынках. Так, цвет мяса при облучении его ультрафиолетом по мере постепенной порчи изменяется от красно-фиолетового до зеленовато-голубоватого, рыбы – от серого до желто-зеленого, молока – от зеленовато-желтого до синего и т.п.
По виду свечения микропрепаратов, рассматриваемых через биологический микроскоп под действием УФ освещения, можно распознавать виды возбудителей инфекционных заболеваний: туберкулеза, сибирской язвы, сальмонеллеза и пр. Люминесцентный анализ позволяет также определять наличие подкожных кровоизлияний (по тушению люминесценции гемоглобином), аномалии в пигментации (по отсутствию свечения пигментированной кожи) и многое другое.
4.2.11 Лазерное излучение
Оптическими квантовыми генераторами, или лазерами, называют устройства, создающие когерентные электромагнитные волны в оптическом диапазоне на основе вынужденного излучения. В зависимости от применяемого рабочего вещества различают кристаллические, газовые и жидкостные лазеры. Рассмотрим принцип действия кристаллического (рубинового) лазера (рис4.2.6).
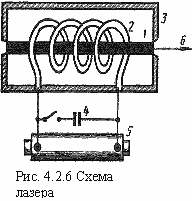
Рабочим веществом является синтетический рубин-окись алюминия Аl2О3 с очень малой (0,05%) примесью окиси хрома Сr2O3. Из рубина изготавливают цилиндрический стержень 1 (диаметром до 2 см и длиной до 50 см). Строго параллельные торцы стержня тщательно отполированы и посеребрены настолько, что один из них полностью зеркален, а другой частично прозрачен - пропускает около 10% излучения. Рубиновый стержень окружен спиральной импульсной лампой 2, помещенной в отражающий кожух 3. Лампа дает яркие вспышки сине-зеленового света при разрядах конденсатора 4, соединенного с индукционной катушкой 5.
В генерировании лазерного света (луча 6) участвуют только ионы хрома. На рис.4.2.7 изображена трехуровневая схема генерирования: 1 – нормальный энергетический уровень, 2 и 3 – возбужденные уровни.
Зеленый свет импульсной лампы с длиной волны 560 нм переводит ионы хрома с энергетического уровня 1 на уровень 3. Вспышка лампы создает на некоторое время значительную перенаселенность уровня 2 по сравнению с уровнем 1. Затем с уровня 2 начинают спонтанные переходы ионов хрома на уровень 1, сопровождающиеся испусканием фотонов частотой
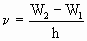 , | (4.2.25) |
соответствующей красному свету (длина волны 690 нм). Фотоны, летящие под углом к оси рубинового стержня, выходят из него через прозрачную боковую поверхность и больше в работе лазера не участвуют. Фотоны же, летящие вдоль оси, претерпевают несколько отражений от торцов стержня, вызывая почти мгновенный переход 2 ® 1 всех возбужденных ионов хрома, сопровождающийся индуцированным излучением той же частоты ν. Когда усиливающийся осевой поток фотонов достигает достаточной мощности, он выходит через частично прозрачный торец стержня в виде узкого высококогерентного монохроматического луча 6 (см. рис. 4.2.6)
4.2.12 Физические свойства лазерного излучения.
Мощность. Твердотельный неодимый лазер генерирует импульсы мощностью до 2,5 1013Вт. (Для сравнения – мощность Красноярской ГЭС равна 6 109Вт) Мощность газовых лазеров значительно ниже (до 50 кВт), однако их преимущество в том, что их излучение происходит непрерывно.
Интенсивность излучения. Угол расходимости лазерного пучка очень мал, и поэтому интенсивность светового потока почти не убывает с расстоянием. Импульсные лазеры могут создавать интенсивности света до 1014Вт/м2. Для сравнения, среднее значение интенсивности солнечного света вблизи поверхности земли всего лишь 103Вт/м2.
Когерентность. Согласованное протекание во времени и в пространстве нескольких волновых процессов, проявляющееся при их сложении. Колебания называются когерентными, если разность фаз между ними остается постоянной во времени. Когерентное лазерное излучение можно сфокусировать в пятно диаметром, равным длине волны этого излучения, что позволяет увеличивать и без того большую интенсивность лазерного пучка света.
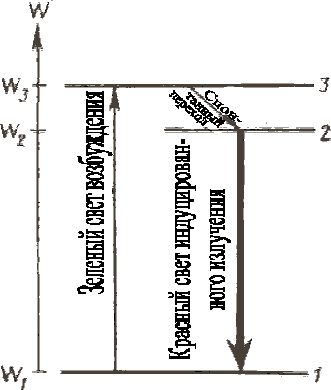
Рис. 4.2.7. Трехступенчатая система генерирования;
1 - нормальный энергетический уровень, 2 и 3 - возбужденные уровни
Монохроматичность. Монохроматическим называют излучение со строго одинаковой длиной волны, однако его может создавать только гармоническое колебание, происходящее с неизменной частотой и амплитудой в течение бесконечно долгого времени. Лазерное излучение обладает высокой степенью монохроматичности. Ширина спектральных линий, создаваемых некоторыми лазерами, достигает 10-7нм, т.е. в тысячи раз уже, чем у обычного света.
Поляризация. В отличие от естественного света лазерное излучение полностью поляризовано.
Направленность излучения. Важным свойством лазерного излучения является его строгая направленность, характеризуемая очень малой расходимостью светового луча, что является следствием высокой степени когерентности. Угол расходимости у многих лазеров доведен примерно до 10-3рад, что соответствует одной угловой минуты. Такая направленность позволяет передавать световые сигналы на огромные расстояния при очень малом ослаблении их интенсивности, что крайне важно при использовании лазеров в системах передачи информации или в космосе.
Напряженность электрического поля. Напряженность электрического поля в световой волне лазерного излучения равна 3 1010В/м, что превышает напряженность поля внутри атома. Для сравнения напряженность поля в световых волнах, создаваемых обычными источниками света, не превышает 104В/м.
Давление. Световое давление для лазерного излучения достигает 1012Па. (Для сравнения световое давление, создаваемое солнечным светом, примерно равно 4 10-6Па. Напомним, что атмосферное давление 105Па). Такое давление позволяет обрабатывать самые твердые материалы - алмаз и сверхтвердые сплавы.
4.2.13 Масса и импульс фотона. Световое давление.
Так как фотон обладает энергией Е=hν, то он должен иметь массу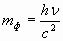 
. Фотон движется со скоростью света с, поэтому его импульс
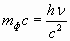 | (4.2.26) |
Видно, что с увеличением частоты излучения ν масса и импульс фотона возрастают.
Масса фотона оказывается крайне малой, однако для жесткого рентгеновского излучения она уже сравнима с массой электрона, а для гамма-излучения даже превышает массу электрона.
Поскольку фотоны обладают импульсом, световой поток должен оказывать давление на преграды, встречающиеся на его пути. Световое давление обычно рассчитывается на основе квантовой теории, рассматривая свет как поток фотонов. Расчет дает следующее выражение для светового давления р:
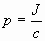 | (4.2.27) |
где J- интенсивность монохроматического пучка света J = Nhν (N- число фотонов, падающих на площадь 1 м2 за 1 с.)
Экспериментально световое давление было впервые обнаружено и измерено в 1900г П.Н.Лебедевым.
Значения светового давления, полученные Лебедевым на опыте, совпали с теоретически рассчитанными значениями. В частности оказалось, что давление света на отражающую поверхность (блестящую пластинку) вдвое больше, чем на поглощающую (зачерненную пластинку).
4.2.14 Эффект Комптона
Взаимодействие фотонов с электронами впервые наблюдалось на опыте в 1923г., американским физиком А.Х.Комптоном. Он обнаружил, что
при рентгеновском облучении вещества, содержащего свободные или слабо связанные электроны, происходит рассеяние рентгеновских лучей, сопровождающееся увеличением длины волны рассеянного излучения (эффект Комптона или комптоновское рассеяние).
Схема эффекта Комптона изображена на рис.4.2.8 Фотон, имеющий энергию hν 0, сталкиваясь с электроном e, передает ему часть своей энергии. В результате электрон отскакивает в сторону, а фотон изменяет направление своего движения (рассеивается). Очевидно, что энергия рассеянного фотона hν< hν0 (поскольку часть энергии фотон передал электрону). Следовательно, ν <ν0, а λ>λ0 (где λ и λ0-длины волн рассеянного и падающего фотонов)
Опыт и теории показывают, что увеличение длины волны рассеянного фотона Δλ = λ- λ0 зависит только от угла рассеяния Θ:
| Δλ = 2λкsin2(Θ/2), | (4.2.28) |
где постоянная λ к называется комптоновской длиной волны и равна
λк=2,43·10-12м.
Комптоновское рассеяние, подобно фотоэффекту, не укладывается в рамки классической теории, согласно которой длина волны излучения при рассеянии остается без изменения. Если же фотон рассматривать с точки зрения квантовой теории как частицу с импульсом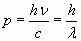 
и взаимодействие с электронами по закону упругого соударения, то явление получает удовлетворительное объяснение.
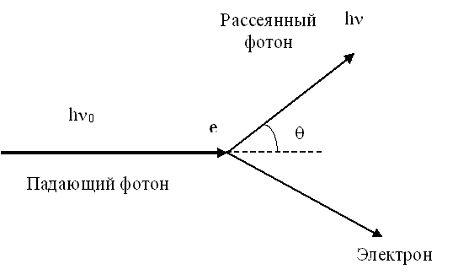
Рис.4.2.8. Схема эффекта Комптона
4.2.15. Модель атома Бора
Электромагнитные излучения - видимый свет, радиоволны, инфракрасное и ультрафиолетовое излучения - могут поглощаться и испускаться атомами. Этим, в частности, объясняется окраска окружающих нас тел.
Если нагреть газ, то окажется, что такое тело обладает линейчатым спектром испускания (излучаемые электромагнитные волны занимают узкие полоски в спектре). Спектром обычно называют зависимость интенсивности излучения от длины или частоты волны. Газ того или иного сорта представляет собой совокупность атомов данного вещества, слабо взаимодействующих друг с другом. Швейцарский ученый И.Бальмер установил (1885), что длины волн известных в то время девяти линий спектра водорода удовлетворяют формуле:
 | (4.2.28) |
где R' = 10973731,77 м-1 - постоянная Ридберга, n = 3, 4, 5, …
Так как 
, то для частот соотношение (4.2.28) примет вид:
 | (4.2.29) |
где R = R'·с.
Все линии спектра, определяемые формулой (4.2.29), называются серией Бальмера. Формулы вида (4.2.29) могут быть записаны и для линий других частей спектра (серии Пашена для ИК части спектра, серией Лаймана для УФ части спектра и др.). Поэтому для всех спектральных линий водорода были предложены единые формулы:
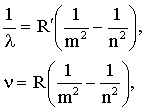 | (4.2.30) |
где m и n - целые числа, причем для данной серии n = m + 1, m + 2, m + 3, … и т.д.
Для серии Лаймана m = 1, для серии Бальмера m = 2, для серии Пашена m = 3 и т.д.
Исторически первой моделью строения атома была планетарная классическая модель Резерфорда. Опираясь на данные экспериментальных исследований рассеяния быстрых частиц в веществе, Резерфорд пришел к выводу, что строение атома можно уподобить планетной системе, где в центре находится компактное положительно заряженное ядро, в котором сосредоточена почти вся масса атома, а по орбитам вокруг ядра вращаются электроны. Число электронов равно порядковому номеру элемента в таблице Менделеева. Силы, связывающие между собой ядро и электроны - электрической природы.
Однако модель Резерфорда несла в себе серьезные противоречия. Согласно законам классической электродинамики, электрон, вращающийся по орбите, представляет собой высокочастотный переменный ток, который порождает переменное магнитное поле. Следовательно, должна возникать электромагнитная волна, которая будет уносить энергию электрона в атоме. Такой электрон тогда должен непрерывно изменять (уменьшать) свою орбиту и в конечном счете упасть на ядро. Спектр излучения должен быть не дискретным (линейчатым), а сплошным, что на практике не наблюдается.
Поэтому Нильс Бор предложил (1913) более последовательную квантовую модель строения атома водорода. Он развил модель Резерфорда, дополнив ее рядом положений, опирающихся на опытные данные - постулатов.
Первый постулат Бора (постулат стационарных состояний): существуют стационарные состояния электронов в атоме, находясь в которых, они не излучают энергию.
Этим состояниям соответствуют стационарные электронные орбиты. Для таких орбит справедливо правило квантования Бора: в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантованные (дискретные) значения момента импульса:
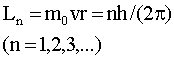 | (4.2.31) |
где m0 и v - масса и скорость электрона, r - радиус его орбиты.
Второй постулат (правило частот): при переходе атома из одного стационарного состояния в другое испускается или поглощается один фотон.
Излучение происходит при переходе атома из состояния с большей энергией в состояние с меньшей энергией, т.е. при переходе электрона с орбиты более удаленной от ядра на ближнюю к ядру стационарную орбиту. Поглощение фотона сопровождается переходом атома в состояние с большей энергией, в результате электрон переходит на более удаленную от ядра стационарную орбиту. Изменение энергии атома, связанное с излучением или поглощением фотона, пропорционально частоте:
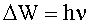 | (4.2.32) |
Если Wm и Wn - энергия атома в двух стационарных состояниях, то формулу (4.2.32) можно представить так:
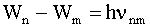 | (4.2.33) |
В атоме водорода вокруг положительно заряженного ядра движется один электрон. Ядро, в силу его большой, по сравнению с электроном, массы, можно считать неподвижным, а орбиту электрона - круговой. Центростремительной силой, удерживающей электрон в атоме, является кулоновская сила притяжения ядра и электрона:
 | (4.2.34) |
Используя (4.2.31) и (4.2.34), имеем для радиуса орбиты электрона в атоме водорода:
 | (4.2.35) |
Ясно, что этот радиус зависит от квантового числа n = 1, 2, 3,…. Для ближайшей к ядру орбиты (n = 1) получим r1 = 0,53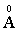 
. По сути, эта величина определяет размер атома водорода в основном состоянии.
Радиусы стационарных орбит относятся между собой как квадраты чисел натурального ряда: 1:4:9:16 и т.д.
Определим сейчас полную энергию электрона в атоме. Она слагается из кинетической энергии движения электрона по орбите и потенциальной энергии притяжения электрона к ядру. Используя (4.2.34), получим для кинетической энергии:
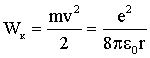 | (4.2.36) |
Потенциальная энергия притяжения двух разноименных зарядов равна:
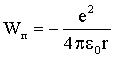 | (4.2.37) |
Суммируя (4.2.36) и (4.2.37), получаем:
 | (4.2.38) |
Подставляя в (4.2.38) выражение для радиуса (4.2.35), имеем:
 | (4.2.39) |
Согласно этому выражению, можно рассчитать энергию электрона для любой стационарной орбиты. Для n = 1 W1 = –13,55 эВ. Полная энергия электрона, находящегося на стационарной орбите, называется уровнем энергии атома. Минимум энергии атома - значение W1 = –13,55 эВ, максимум энергии W = 0 - при движении электрона по столь далекой орбите (n = ∞), на которой электрон уже не связан с ядром (атом превращается в ион).
Самопроизвольный переход электрона на более далекую орбиту (более высокий энергетический уровень) невозможен. Для такого перехода атому извне необходимо сообщить определенную энергию (возбудить атом). Так, переход электрона с первой стационарной орбиты на вторую происходит при поглощении атомом кванта с энергией 10,17 эВ. Таким образом, атом может излучать или поглощать волны только вполне определенных частот, чем и обусловлен линейчатый характер спектра атома водорода.
Нормальным состоянием атома является такое, при котором электрон движется по ближайшей к ядру орбите. Атом в этом состоянии не может излучать энергию. Все остальные уровни энергии атома водорода называются возбужденными.
|
|