или физический закон
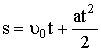


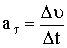
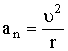

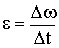
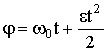
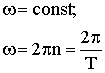
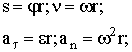
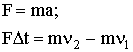
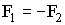
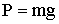
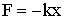
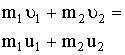
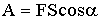
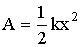




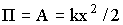
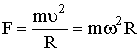
а) материальной точки
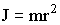
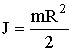

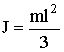
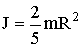

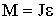
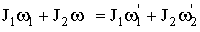
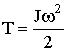
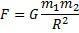
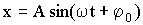
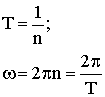
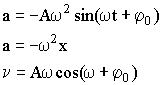
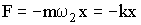

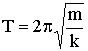
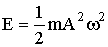
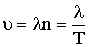
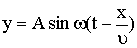
| Наименование величины или физический закон | Формула |
|---|---|
| Путь при равнопеременном движении | 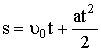 |
| Скорость равнопеременного движения |  |
| Ускорение в равнопеременном движении |  |
| Тангенциальное (касательное) ускорение | 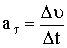 |
| Нормальное (центростремительное) ускорение | 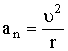 |
| Полное ускорение |  |
| Ускорение угловое | 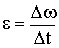 |
| Угол поворота при равнопеременном вращении | 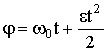 |
| Угловая скорость точки при равномерном обращении по окружности, где n - частота обращения; Т - период обращения | 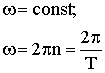 |
| Связь между линейными и угловыми величинами при вращательном движении | 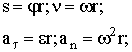 |
| Второй закон Ньютона для поступательного движения | 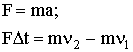 |
| Третий закон Ньютона | 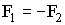 |
| Сила тяжести (g = 9,8 м/с2- ускорение свободного падения) | 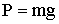 |
| Сила упругости (закон Гука) | 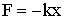 |
| Закон сохранения импульса (количества движения) для изолированной системы двух тел | 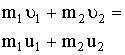 |
| Механическая работа постоянной силы | 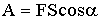 |
| Работа упругой силы ( в пределах закона Гука) | 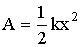 |
| Мощность |  |
| Кинетическая энергия тела |  |
| Потенциальная энергия тела, поднятого над поверхностью Земли |  |
| Полная энергия тела (в изолированной системе) |  |
| Энергия упругодеформированного тела (работа силы упругости) | 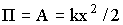 |
| Центростремительная сила | 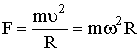 |
| Момент инерции: а) материальной точки | 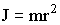 |
| б) сплошного цилиндра или диска относительно оси, совпадающей с геометрической осью | 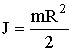 |
| в) однородного тонкого стержня относительно оси, проходящей через центр |  |
| г) однородного стержня относительно оси, проходящей через один из концов | 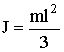 |
| д) однородного шара | 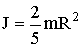 |
| Момент силы (где l - плечо силы ) |  |
| Основной закон динамики вращательного движения | 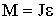 |
| Закон сохранения момента количества движения (импульса) для изолированной системы двух тел | 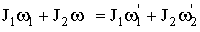 |
| Кинетическая энергия вращающегося тела | 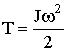 |
| Закон всемирного тяготения (где G = 6,67·10-11 м3/(кг·с)- гравитационная постоянная) | 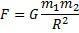 |
| Уравнение гармонического колебания(где А-амплитуда колебаний, ω-циклическая или круговая частота, φ0-начальная фаза) | 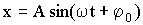 |
| Соотношение между периодом, частотой и круговой (циклической) частотой | 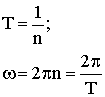 |
| Скорость и ускорение точки при гармонических колебаниях | 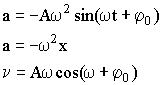 |
| Сила, действующая на колеблющуюся материальную точку | 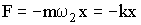 |
| Период гармонических колебаний математического маятника |  |
| Период колебаний пружинного маятника | 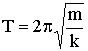 |
| Полная энергия колеблющейся материальной точки | 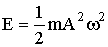 |
| Зависимость между скоростью распространения волны, длиной волны, частотой и периодом колебаний точек среды | 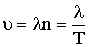 |
| Уравнение волны | 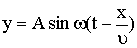 |
Пример 1.У светофора трактор, движущийся равномерно со скоростью 18 км/ч, обогнал автомобиль, который из состояния покоя начал двигаться с ускорением а=1,25 м/с2. Определить:1) на каком расстоянии от светофора автомобиль обгонит трактор; 2) скорость автомобиля при обгоне. Решение. 1. Путь, пройденный автомобилем, определяется формулой
где а – ускорение автомобиля, м/с2; t – время, в течение которого автомобиль обгонит трактор, с. За время t такой же путь s пройдёт трактор, движущийся равномерно, т.е.
где К моменту обгона трактора автомобиль и трактор пройдут одинаковый путь s. Приравнивая правые части (1), (2), получаем
Путь s, пройденный автомобилем от светофора до обгона, получим из (1), подставив вместо t выражение (3'):
Проверим формулу (4):
Выразим в СИ скорость трактора:
Вычислим искомое расстояние от светофора до места обгона:
2. Скорость автомобиля, движущегося равноускоренно, выражается формулой
Вычислим искомую скорость автомобиля:
Пример 2.На гладкой горизонтальной плоскости находится тело массой m1=250 г (рис. 1). Тело массой m2=400 г подвешено на нити, перекинутой через блок и привязанной к телу m1. Пренебрегая массой блока и трением, определить: 1) силу натяжения нити; 2) ускорение тел.
Решение. 1. На тело массой m2 действуют сила тяжести
где а – ускорение тела, g – ускорение свободного падения. На тело m1 действуют сила тяжести Второй закон Ньютона в скалярном виде для тела m1 имеет вид
Чтобы найти ускорение, сложим левые и правые части (1) и (2):
Выразим массу тел m1 и m2 в единицах СИ: m1=0,25 кг и m2=0,4 кг. Вычислим ускорение а по формуле (3):
2. Силу натяжения нити найдем, подставив полученный результат в уравнение (2):
Пример З.Тело, массой m1=1 кг вращается на тонком стержне в вертикальной плоскости. Частота вращения равна n=2 c-1, длина стержня R=12,5 см. Определить силу натяжения стержня: 1) в верхней и 2) в нижней точках.Решение. 1. На тело в верхней точке действуют: сила тяжести P=mg и сила N натяжении стержня (рис. 2). В результате действия двух сил тело движется по окружности, т. е, с центростремительным ускорением
где ω – угловая скорость, R – радиус траектории. Учитывая, что
где n – частота вращения. Направление сил N и Р совпадает с вектором ацс, поэтому второй закон Ньютона запишем в проекции на направление сил:
или с учетом (2)
откуда
Выразим в СИ числовые значения R и g: R=0,125 м; g=9,81 м/c2.
Вычислим по формуле (5) искомое натяжение стрежня в верхней точке траектории:
2.В нижней точке траектории на тело действуют ( рис.3) те же силы mg и N. Однако сила mg в данном случае направлена противоположно вектору aцс. В связи с этим второй закон Ньютона имеет вид
откуда
После подстановки имеем:
Пример 4.Подъемный кран за время t=6 ч поднимает строительные материалы массой m=3000 т на высоту h=15 м. Определить мощность двигателя подъемного крана, если его коэффициент полезного действия η=0,8.Решение. Подъемный кран, поднимая груз на высоту h, увеличивает его потенциальную энергию. Работа А, совершаемая двигателем подъемного крана, идет па подъём груза и на работу против сил трения в механизмах. Полезная работа Ап двигателя равна увеличению потенциальной энергии груза:
где g— ускорение свободного падения. Коэффициент полезного действия η равен отношению полезной мощности Nп ко всей потребляемой мощности N:
Учитывая, что
Мощность двигателя равна
Проверим формулу (4):
Выпишем в СИ числовые значения ряда величин, входящих в (4):
Вычислим искомую мощность двигателя:
Пример 5.Тело массой m=200 г прикреплено к нити и вращается по окружности радиусом R1=80 см с постоянной линейной скоростью v1=150 см/с. При вращении нить укорачивается на длину l=30 см. Определить: 1) новую скорость вращения и 2) частоту вращения.Решение. 1. При равномерном вращении тела уменьшение длины нити создается силой F, направленной вдоль радиуса R1. Плечо R этой силы равно нулю, следовательно, момент силы M=FR также равен нулю. Вращение тела, свободного от действия моментов сил, подчиняется закону сохранения момента импульса:
где j1 – момент инерции, ω1 – угловая скорость тела в начальный момент времени; j2 и ω2 — то же в конечный момент времени. Следовательно, начальный момент импульса j1 ω1 равен моменту импульса j2 ω2 тела после укорачивания нити. Считая, что тело представляет собой материальную точку, определим его момент инерции:
где R — радиус окружности, по которой вращается тело. Угловую скорость выразим через линейную:
Для начального момента времени по формулам (2) и (3) получим
После укорачивания нити
Подставляя в (1) выражения (4) и (5), получаем
После преобразований с учетом того, что R2=R1 – l, окончательно имеем
или
Проверим расчетную формулу (8):
Выразим числовые значения величин в СИ: v1=1,50 м/с; R1=0,80 м; l=0,30 м. Вычислим искомую конечную скорость:
2. Для определения частоты вращения n2 после укорачивания нити воспользуемся формулами
откуда
Проверим формулу (10):
Вычислим искомую конечную частоту вращения:
Пример 6.Диск, катившийся со скоростью v1=3 м/с, ударился о стену и покатился назад со скоростью v2=2 м/с. Масса диска равна m=3 кг. Определить уменьшение кинетической энергии диска.Решение. Кинетическая энергия диска равна сумке кинетических энергий поступательного и вращательного движении:
Здесь
где m — масса диска;
R — радиус окружности диска. Подставив в (1) выражения для Епост, Евр, j и ω, получим
Выражение, полученное нами, можно использовать для записи полной кинетической энергии Е1 до удара о стену и полной кинетической энергии Е2 после взаимодействия со стеной:
Разность кинетических энергий
Подставив данные условия задачи, вычислим искомую разность энергий:
Знак «минус» показывает, что произошло уменьшение кинетической энергии диска. Пример 7.Точка совершает гармонические колебания согласно равнению . Определить скорость и ускорение точки через 1/6 с от начала колебаний. . Определить скорость и ускорение точки через 1/6 с от начала колебаний.
Решение. Запишем уравнение гармонических колебаний в общем виде:
где х – смещение точки, А – амплитуда, ω – круговая частота, t – время. По определению скорость равна производной от смещения по времени:
Подставив (1) в (2), продифференцируем полученное выражение:
По определению ускорение времени равно производной от скорости по времени:
Подставив (3) в (4), продифференцируем полученное выражение:
Из сравнения уравнения
Вычислим искомые скорость и ускорение точки:
|