или физический закон
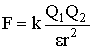
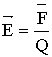

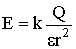
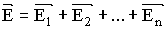
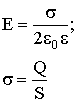
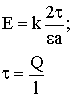


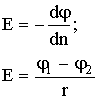

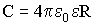
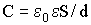
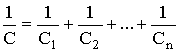


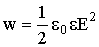
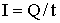

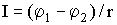
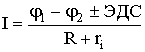
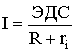
- в узле разветвленной цепи сумма токов равна нулю;
- в замкнутом контуре разветвленной цепи сумма падений напряжения на отдельных участках равна сумме ЭДС источников тока, включенных в контур
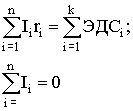
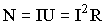

| Наименование величины или физический закон | Формула |
|---|---|
| Закон Кулона (где k=9·109H·м2/Кл2 - электрическая постоянная; ε - диэлектрическая проницаемость среды; e=1,60·10-19Кл - заряд электрона, протона; me=9,11·10-31кг - масса электрона; mр=1,67·10-27кг - масса протона) | 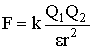 |
| Напряженность электрического поля | 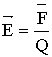 |
| Теорема Остроградского-Гаусса (ε0=8,85·10-12Ф/м) |  |
| Напряженность поля точечного заряда | 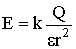 |
| Напряженность поля, созданного двумя и более точечными зарядами | 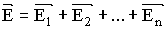 |
| Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью | 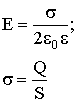 |
| Напряженность поля, создаваемого бесконечной равномерно заряженной нитью | 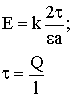 |
| Потенциал поля |  |
| Потенциал поля точечного заряда |  |
| Связь между напряженностью и потенциалом неоднородного и однородного поля | 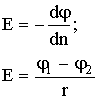 |
| Электроемкость уединенного проводника |  |
| Электроемкость сферы | 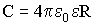 |
| Электроемкость плоского конденсатора | 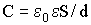 |
| Электроемкость последовательного соединения конденсаторов | 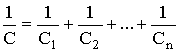 |
| Электроемкость параллельного соединения конденсаторов |  |
| Энергия конденсатора |  |
| Объемная плотность энергии электрического поля | 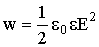 |
| Сила постоянного тока | 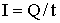 |
| Плотность тока |  |
| Закон Ома для однородного участка цепи | 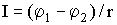 |
| Закон Ома для неоднородной цепи | 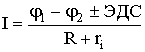 |
| Закон Ома для замкнутой цепи | 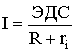 |
Законы Кирхгофа:
| 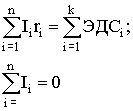 |
| Мощность тока | 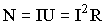 |
| Закон Джоуля-Ленца |  |
Примеры решения задачПример 18.На шёлковой нити в воздухе подвешен маленький положительно заряженный шарик массой m = 90 мг. Если ниже шарика на расстоянии r = 1 см от него поместить равный, но отрицательный заряд, то сила натяжения нити увеличится в три раза. Определить заряд шарика. Решение. На подвешенный шарик первоначально действуют две силы: сила тяжести Р, направленная вертикально вниз, и сила натяжения нити Т1 направленная вдоль нити вверх. Шарик при этом находится в равновесии и, следовательно,
После того как к шарику был поднесен снизу отрицательный заряд, на него кроме силы тяжести
Р действует сила Fк, направленная вниз и определяемая по закону Кулона (рис. 4).
В этом случае сила натяжения
Выразив в (2) Fк по закону Кулона к силу тяжести P через массу тела m и ускорение свободного падения g получим
откуда
Проверим единицы правой и левой частей расчетной формулы (3):
Выпишем числовые значения в СИ: m = 9·10 -5 кг; r = 10-2 м; еε = 1; g = 9,81 м/с2; ε0 = 8,85·10-12 Ф/м. Вычислим искомый заряд:
Пример 19.Два положительных заряда Q=5 нКл и Q2 = 3 нКл находятся на расстоянии d=20 см друг от друга. Где надо поместить третий отрицательный заряд Q, чтобы он оказался в равновесии ? Решение. На заряд Q3 действуют две силы: F1, направленная к заряду Q1 и F2, направленная к заряду Q2. Заряд Q3 будет находиться в равновесии, если равнодействующая этих сил равна нулю:
т. е, силы F1 и F2 должны быть равны по модулю в направлены в противоположные стороны. Силы будут противоположны по направлению только в том случае, если заряд Q3 находится в точке на отрезке прямой, соединяющем заряды Q1, и Q2 (рис. 5). Для равенства сил необходимо, чтобы заряд Q3 находился ближе к меньшему заряду Q2. Так как векторы сил F1, и F2 направлены по одной прямой, то векторное равенство (1) можно, опуская знак «минус», заменить скалярным:
Выразив силы F1, и F2 по закону Кулона, (2) запишем в виде
или
Извлекая из обеих частей равенства квадратный корень, находим
Выпишем числовые значения величии, входящих в (3) в СИ: Q1 = 5·10 -9 Кл; Q2 = 3·10 -9 Кл; d = 0,2 м. Вычисления:
Из двух значений корня r1 = 11,3 см. и r2 = -11,3 см берем первый, так как второй не удовлетворяет условию задачи, Итак, для того чтобы заряд Q3 находился в равновесии, его надо поместить на прямой, соединяющей заряды Q1 и Q2 на расстоянии r = 11,3 см. от заряда Q1 (рис. 5). Пример 20.В вершинах равностороннего треугольника со стороной а = 20 см находятся заряды Q1 = Q2 = -10 нКл и Q3 = 20 нКл. Определить силу, действующую на заряд Q = 1 нКл, расположенный в центре треугольника.
На заряд Q, расположенный в центре треугольника, действуют три силы:
где F1 — сила, действующая на заряд Q со стороны заряда Q1; F2 — сила, действующая на заряд Q со стороны заряда Q2 . Результирующая этих сил
Кроме этой силы заряд Q испытывает действие силы F3, со стороны заряда Q3. Искомую силу F, действующую на заряд Q, найдем как результирующую сил F´ и F3:
Так как F´ и F3 направлены по одной прямой и в одну сторону, то это векторное
равенство можно заменить скалярным:
Выразив здесь F1 и F2 по закону Кулона, получим
Из рис. 6 следует, что
С учетом этого формула (3) примет вид :
Проверим расчётную формулу (4):
Выпишем числовые значения величии в СИ: Q1 = Q2 = -1·10 -8 Кл; Q3 = 2·10 -8 Кл; ε = 1; ε0 = 8,85·10 -12Ф/м; a = 0,2 м. Вычислим искомую силу:
Примечание. В формулу (4), подставлены модули зарядов, поскольку их знаки учтены при выводе этой формулы. Пример 21.Электрическое поле создано в вакууме двумя точечными зарядами Q1 = 2 нКл Q2 = -3 нКл. Расстояние между зарядами d = 20 см. Определить: 1) напряженность и 2) потенциал электрического поля в точке, находящейся на расстоянии r1 = 15 см от первого и r2 = 10 см. от второго заряда (рис. 7).
Согласно принципу суперпозиции электрических полей каждый заряд создает поле независимо от присутствия в
пространстве других зарядов. Поэтому напряженность Е результирующего электрического поля в искомой точке может
быть найдена как геометрическая сумма напряженностей Е1 и Е2 полей, создаваемых каждым зарядом
в отдельности:
Вектор Е направлен по прямой, соединяющей заряд Q1 и точку А, от заряда Q1, так как он положителен; вектор Е2 направлен по прямой, соединяющей заряд Q2 и точку А, к заряду Q2 так как заряд отрицателен. Модуль вектора Е найден по теореме косинусов:
где α — угол между векторами Е1 и Е2. Из треугольника со сторонами d, r1 и r2 найдем
Подставляя выражение Е1, из (1), Е2 из (2) в (3), получаем
Выпишем числовые значения величии в СИ: Q1 = 2·10 -9 Кл; Q2 = -3·10 -9 Кл; d = 0,2 м; r1 = 0,15 м; r2 = 0,1 м; ε = 1; ε0 = 8,85·10 -12Ф/м; Вычислим значение cosα по (4):
Вычислим искомую напряженность:
Примечание. В формулу (5) подставлены модули зарядов, так как их знаки учтены при выводе этой формулы. 2. Потенциал в точке А поля равен алгебраической сумме потенциалов, созданных в этой точке зарядами Q1 и Q2:
Вычислим искомый потенциал:
Пример 22.Какова скорость обращения электрона вокруг протона в атоме водорода, если орбиту электрода считать круговой с радиусом r = 0,53· 10-8 см Решение. При обращении электрона по круговой орбите центростремительной силой является сила электрического притяжения электрона и протона, т. е. справедливо равенство
Центростремительная сила определяется по формуле
где m — масса электрона, движущегося по окружности; u — скорость обращения электрона; r — радиус орбиты. Сила Fк взаимодействия зарядов согласно закону Кулона выразится формулой
где Q1 и Q1— абсолютные значения зарядов; ε — относительная диэлектрическая проницаемость;ε0 — электрическая постоянная. Подставляя в (l) выражения Fцс из (2) и Fк из (3), а также учитывая, что заряд протона и электрона, обозначаемый буквой е, одинаков, получаем
Выпишем числовые значения величии в СИ: e = 1,6·10 -19 Кл; ε = 1; ε0 = 8,85·10 -12Ф/м; r = 0,53·10 -10 м; m = 9,1·10 -31 кг. Вычислим искомую скорость:
Пример 23.Потенциал φ в точке поля, расположенной на расстоянии r = 10 см от некоторого заряда Q, равен 300 В. Определить заряд и напряжённость поля в этой точке. Решение. Потенциал точки поля, созданного точечным зарядом, определяется по формуле
где ε0 — электрическая постоянная; ε — диэлектрическая проницаемость. Из формулы (1) выразим Q:
Для любой точки поля точечного заряда справедливо равенство
Из этого равенства можно найти напряженность поля. Выпишем числовые значения величии, выразив их в СИ: r = 0,1 м; φ1 = 300 В; ε = 1; ε0 = 8,85·10 -12Ф/м. Подставим числовые значения в (2) и (3):
Пример 24.Электрон, начальная скорость которого u0 = 2 Мм/с, влетел в однородное электрическое поле с напряженностью E = 10 кВ/м так, что вектор начальной скорости перпендикулярен линиям напряженности. Определить скорость электрона по истечении времени t = 1 нс. Решение. На электрон, находящийся в электрическом поле, действует сила
где е — заряд электрона. Направление этой силы противоположно направлению силовых линий поля. В данном случае сила направлена перпендикулярно скорости u0. Она сообщает электрону ускорение
где m - масса электрона.
где u1 — скорость, которую получает электрон под действием сил поля. Скорость u1 найдем по формуле
Так как скорости u0 и u1 взаимно перпендикулярны, то результирующая скорость
Подставляя в (4) выражение скорости по (3) и учитывая (1) и (2) получаем:
Выпишем числовые значения величин, входящих в (5) в СИ: е = 1,6·10 -19 Кл; m = 9,11·10 -31 кг ; t = 105·10 -9 с; u0 = 2·10 6 м/с; Е = 10·10 4 В/м. Вычислим искомую скорость:
Пример 25.В точке М поля точечного заряда Q = 40 нКл находится заряд Q1 = 1 нКл. Под действием сил поля заряд перемешается в точку N, расположенную вдвое дальше от заряда Q, чем NM. При этом совершается работа А = 0,1 мкДж. На какое расстояние переместится заряд Q1? Решение. Работа сил поля по перемещению заряда выражается формулой
где Q1 – перемещающийся заряд; ΦM – потенциал точки М поля; ΦN – потенциал точки N поля. Так как поле создано точечным зарядом Q, то потенциалы точек начала и конца пути выразятся формулами:
где rM и rN – расстояние от заряда Q до точек M и N. Подставляя выражения для φM и φN из (2) и (3) в (1), получаем
По условию задачи rN = 2rM.Учитывая это, получаем rN - rM = rM. Тогда
Выпишем числовые значения величин в СИ: Q1 = 1·10 -9 Кл; Q = 4·10 -8 Кл; А = 1·10 -7 Дж; ε0 = 8,85·10 -12Ф/м . Вычислим искомое расстояние:
Пример 26.Электрон прошел ускоряющую разность потенциалов U = 800 B. Определить скорость, приобретенную электроном. Решение. По закону сохранения энергии кинетическая энергия Т, приобретенная зарядом (электроном), равна работе А, совершаемой электрическим полем при перемещении электрона:
Работа сил электрического поля при перемещении электрона
где e — заряд электрона. Кинетическая энергия электрона
где m- масса электрона;u- его скорость.
Подставив в (1) выражения Т и А из (2) и (3), получим
Выпишем числовые значения величин входящих в (4), в СИ: U=800 В; e = 1,6·10 -19 Кл; m = 9,11·10 -31 кг. Вычислим искомую скорость:
Пример 27.Плоский конденсатор, расстояние между пластинами которого d1 = 3 см, заряжен до разности потенциалов U1 = 300 B и отключен от источника. Каким будет напряжение на пластинах конденсатора, если его пластины раздвинуть до расстояния d2 = 6 см? Решение. До раздвижения пластин емкость плоского конденсатора
где ε— диэлектрическая проницаемость вещества, заполняющего пространство между пластинами конденсатора; ε0 — электрическая постоянная; S — площадь пластин конденсатора. Напряжение на пластинах конденсатора
где Q — заряд конденсатора. Подставляя в (2) выражение емкости конденсатора из (1),находим
Аналогично получим напряжение между пластинами после их раздвижения:
В выражениях (3) и (4) заряд Q одинаков, так как конденсатор отключен от источника напряжения и никаких потерь заряда не происходит.
Разделив почленно (3) на (4) и произведя сокращения, получим
Выпишем числовые значения в СИ: U1 = 300 В; d1 = 0,03 м; d2 = 0,06 м. Вычислим
Пример 28.Плоский конденсатор с площадью пластин S = 50 см2 и расстоянием между ними d = 2 мм заряжен до разности потенциалов U = 100 В. Диэлектрик — фарфор. Определить энергию поля и объемную плотность энергии поля конденсатора. Решение. Энергия конденсатора может быть определена по формуле
где С — емкость конденсатора; U — разность потенциалов, до которой заряжены его пластины. Но
где ε - диэлектрическая проницаемость среды, заполняющей, пространство между пластинами; ε0 — электрическая постоянная (ε0 = 8,85·10-12 Ф/м). Подставив выражение С по формуле (2) в формулу (1),получим
Объёмная плотность энергии поля конденсатора — физическая величина, определяемая отношением энергии к объему, и поэтому может быть определена по формуле
где V = Sd – объем пространства между пластинами конденсатора. Запишем числовые значения величин, входящих в (4), в СИ: S = 50·10-4 м2 ; ε = 5 ; d = 2·10-3 м. Вычислим искомые величины по формулам (3) и (4):
Пример 29.Динамомашина питает n = 100 параллельно включенных электроламп сопротивлением r1 = 240 Ом каждая. Сопротивление подводящих проводов r2 = 0,6 Ом. Определить электродвижущую силу динамомашины (ε), если ее внутреннее сопротивление r3 = 0,05 Ом и напряжение на зажимах U = 120 В. Решение. Электродвижущую силу динамомашины определим по закону Ома для полной цепи:
где I – сила тока в цепи; r – сопротивление внешней цепи. Силу тока в цепи найдем по закону Ома для участка цепи:
Подставив в (1) выражение r из (2) и I из (3), получим
Вычислим искомую э.д.с. дииамомашины, подставив в (4) данные условия:
Пример 30.Электродвигатель работает в сети с напряжением U = 120 В. Сила тока в обмотке I = 10 А. Активное сопротивление двигателя r = 3 Ом. Определить мощность и коэффициент полезного действия двигателя. Решение. Мощность двигателя выражается формулой
Коэффициент полезного действия двигателя
где N — полезная мощность. Но
где N2 = I2 r – мощность, расходуемая на нагревание обмоток двигателя. Подставляя в (2) выражения для N1, N и N2, получим
Выпишем числовые значения величин, входящих в (4), в СИ: U = 120 В; I = I0 А; r = 3 Ом. Вычисления:
Пример 31.Термопара, сопротивление которой r1 = 6 Ом, позволяет определить минимальное изменение температуры Δtмин = 0,006 ºC. Найти сопротивление гальванометра чувствительностью I0 = 1,5·10-8 А, подключенного к термопаре. Постоянная термопары k = 0,05 мВ/ºC. Решение. Электродвижущая сила ε, возникающая в термопаре при разности температур
Согласно закону Ома
где I – сила тока в цепи термопары; r1 – полное сопротивление цепи; r2 – сопротивление гальванометра.
Приравнивая правые части (1) и (2), получаем
Но где n – число делений, на которое отклонилась стрелка гальванометра при силе тока I. Подставив указанные выражения Δt и I в (3) и сократив полученное выражение на n, найдем
Выпишем числовые значения величин, входящих (4), а СИ:
|