или физический закон
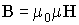
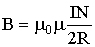
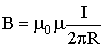
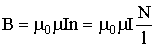
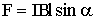
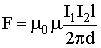
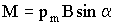

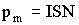
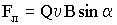

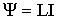
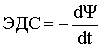
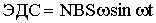


| Наименование величины или физический закон | Формула |
|---|---|
| Связь между индукцией и напряженностью магнитного поля (μ0= 4 π·10-7Гн/м - магнитная постоянная; μ - магнитная проницаемость среды) | 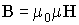 |
| Индукция магнитного поля в центре кругового тока с числом витков N | 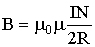 |
| Индукция поля вблизи бесконечно длинного проводника с током | 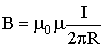 |
| Индукция поля внутри соленоида с током | 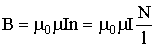 |
| Закон Ампера | 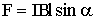 |
| Сила взаимодействия двух прямых токов | 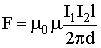 |
| Механический момент, действующий на рамку с током в магнитном поле | 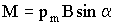 |
| Магнитный момент контура с током |  |
| Магнитный момент рамки с током (короткой катушки) | 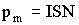 |
| Сила Лоренца | 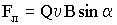 |
| Магнитный поток |  |
| Потокосцепление в контуре с током | 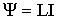 |
| Закон Фарадея-Максвелла | 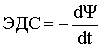 |
| ЭДС переменного тока при вращении рамки в магнитном поле | 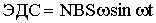 |
| ЭДС самоиндукции |  |
| Индуктивность соленоида (тороида) |  |
Примеры решения задачПример 1.По двум длинным прямолинейным и параллельным проводам, расстояние между которыми d = 4 см, в противоположных направлениях текут токи I1 = 0,3 А, I2 = 0,5 А. Найти магнитную индукцию поля в точке А, которая находится на расстоянии r = 2 см от первого и провода на продолжении линии, соединяющей провода (рис.8). Решение.
На рис. 8 провода расположены перпендикулярно плоскости чертежа. Маленькими кружочками изображены сечения проводив. Условимся, что ток I1, течет к нам, а ток I2 – от нас. Общая индукция В в точке А равна векторной (геометрической) сумме индукции В1, и В1 полей, создаваемых каждым током в отдельности т. е,
Для того чтобы найти направление вектора В1 и В2, проведем через точку А силовые линии магнитных полей, созданных токами I1 и I2. Силовые линии магнитного поля прямого провода с током представляют собой концентрические окружности с центром на оси провода. Направление силовой линии совпадает с движением концов рукоятки правого буравчика, ввинчиваемого во направлению тока (правило буравчика) Поэтому силовая линия магнитного поля тока I1, проходящая через точку А, представляет собой окружность радиусом I1 A, а силовая линии магнитного поля тока I2, проходящая через эту же точку, — окружность радиусом I2 A (на рис. 8 показана только часто этой окружности). По правилу буравчика находим, что силовая линия магнитного ноля тока I1 направлена против часовой стрелки, а тока I2 – по часовой стрелке. Теперь легко найти направления векторов В1 и В2 в точке А: каждый из них направлен по касательной к соответствующей силовой линии в этой точке. Так как векторы В1 и В2 направлены вдоль одной прямой в противоположные стороны, то векторное равенство (1) можно заменить алгебраическим равенством
Индукция магнитного поля тока I, текущего по прямому бесконечно длинному проводу, вычисляется по формуле
где μ0 – магнитная постоянная; μ – магнитная пропицаемость среды, в которой провод расположен; r – расстояние от провода до точки, в которой определяется индукция. Подставив выражения В1 и В2 в равенство (2), получим
или
Запишем в СИ числовые значения некоторых величии: r1 = 0,02 м, r2 = d+r1 = 0,06 м, μ0 = 4π ·10-7 Гн/м, μ = 1. Вычислим искомую индукцию:
Пример 2.Из проволоки диаметром d = 0,01 мм и сопротивлением r = 25 Ом намотан соленоид на картонном цилиндре (витки вплотную прилегают друг к другу). Определить индукцию магнитного поля на оси соленоида, если напряжение на концах обмотки U = 2 В. Решение. Индукция магнитного поля на оси соленоида вычисляется по формуле
Здесь n = 1/d; d – диаметр проволоки; n – число витков на единицу длины соленоида; I – сила тока, текущего по обмотке соленоида. Силу тока, текущего по обмотке, найдём по закону Ома для участка цепи:
Подставим значения n и I в равенство (1):
Выпишем числовые значения величин входящих в (2), в СИ: μ0 = 4π ·10-7 Гн/м, μ = 1. d = 10-4 м. Вычисления:
Пример 3.Прямой провод длиной l = 10 см, по которому течет ток I = 0,5 А, помещен в однородное магнитное поле перпендикулярно силовым линиям. Найти индукцию магнитного поля, если оно действует на прямой провод с силой F = 2,6 мН. Решение. Сила, с которой однородное магнитное поле действует на прямой провод с током, вычисляется по закону Ампера:
где I – сила тока, текущего по проводнику; l – длина проводника; В – индукция магнитного поля, в которое проводник помещён; а- угол между направлениями тока и линий индукции. Из формулы (1) найдем
Выпишем числовые значения величин входящих в (2), в СИ: F = 2,6· 10-3 Н; I = 0,5 А; l = 0,1 м; α = 90º; sinα = 1. Вычисления:
Пример 4.Протон, пройдя ускоряющую разность потенциалов U = 400 В, влетел в однородное магнитное поле с индукцией В = 0,2 Тл и начал двигаться по окружности. Вычислить радиус окружности. Решение. На заряженную частицу, влетевшую в магнитное поле, действует сила Fл, называемая силой Лоренца. Она вычисляется по формуле
Направление силы Лоренца подчиняется, как известно, правилу левой руки. Угол между направлениями v и Fл всегда составляет 90º.
Следовательно, сила Лоренца является центростремительной силой, т.е.
где m – масса протона; R – радиус окружности, по которой движется протон. Тогда
Протон получил скорость, пройдя, ускоряющую разность потенциалов По закону сохранения энергии работа, совершенная полем при перемещении протона, равна кинетической энергии, приобретенной протоном, т, е.
Работа сил электрического поля при перемещении протона определяется по формуле
Кинетическая энергия протона
Подставив выражение А по (З) и выражение Т по (4) в (2), получим
Подставляя выражение для v в (1), находим
Проверим расчетную формулу (6):
Выпишем в СИ числовые значения недостающих величин
Пример 5.Ток, текущий в рамке, содержащей N витков, создаст магнитное поле. В центре рамки индукция поля B = 0,126 Тл. магнитный момент рамки, если ее радиус R = 10 см. Решение. Магнитный момент рамки с током
где I - сила тока в витке; площадь, охватываемая витком
Выпишем числовые значения величин, входящих в (2), в СИ:
Пример 6.Плоская рамка площадью содержащая S = 100 см2, содержащая N = 20 витков тонкого провода, вращается в однородном магнитном поле с индукцией В = 100 мТл. Амплитуда э.д.с. индукции εмакс = 10 В. Определить частоту вращения рамки. Решение. Используя понятие угловой скорости вращении (ω = 2π/T = 2πn, где T – период вращения; n – частота вращения), определим частоту вращения рамки:
Угловую скорость вращения найдем из соотношения
Где ε – мгновенное значение э.д.с. индукции. Амплитудой ε является значение εмакс , соответствующее значению sinωt = 1. Из соотношения (2) имеем
Подставив выражение ω по (3) в (1),получаем
Выразим значения ряда величин, входящих в формулу (4), в СИ:
Пример 7.На немагнитный каркас длиной l = 50 см и площадью сечения S = 3см2 намотан в одни слой провод диаметром d = 0,4 мм так, что витки плотно прилегают друг к другу. Найти: 1) индуктивность получившегося соленоида и 2) магнитный поток, пронизывающий поперечное сечение соленоида при токе силой I = 1 А. Решение. Индуктивность соленоида вычисляется по формуле
где n – число витков, приходящихся на единицу длины соленоида; V – объем соленоида. Число витков n получим, разделив единицу длины на диаметр провода:
Объем соленоида V = Sl, где S – площадь поперечного сечения соленоида; l – длина соленоида. Подставим выражения для n и V в равенство (1):
Выпишем числовые значения величин, входящих в (3), в СИ:
Вычисления:
При наличии тока в соленоиде любое его поперечное сечение пронизывает магнитный поток
где В – магнитная индукция в соленонде. Магнитная индукция соленоида определяется по формуле
Подставив выражения n и В по (2) и (5) в (4), получим расчетную формулу
Выполним вычисления, подставив в расчетную формулу значения величин I, S и d в СИ:
Пример 8.Колебательный контур состоит из плоского воздушного конденсатора с двумя пластинами площадью по S = 100 см ² каждая и катушки с индуктивностью L = 10-5 Гн. Период колебаний в контуре Т = 10-7 с. Определить расстояние между пластинами конденсатора. Решение. Из формулы емкости плоского конденсатора
(ε0 – электрическая постоянная; ε – диэлектрическая проницаемость среды мёжду пластинами конденсатора; S – площадь пластины конденсатора; d – расстояние между пластинами) может быть найдено искомое расстояние
Из формулы Томсона, определяющей период колебаний Т в колебательном контуре,
Выразим некоторые величины, входящие в расчетную формулу (4), в СИ:
Вычислим искомое расстояние:
|