или физический закон
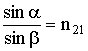

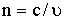
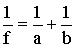

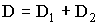
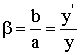
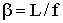
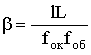
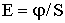


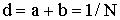
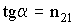
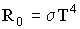
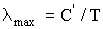
.gif)

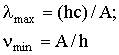
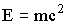
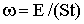
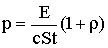
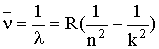
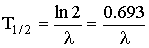

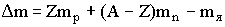
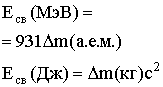
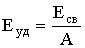
| Наименование величины или физический закон | Формула |
|---|---|
| Закон преломления света (где α - угол падения; β - угол преломления луча) | 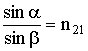 |
| Относительный показатель преломления (где n1, n2 - абсолютные показатели преломления первой и второй среды) |  |
| Абсолютный показатель преломления (где с =3·108м/с2 - скорость света в вакууме; v - скорость света в среде) | 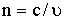 |
| Формула линзы (f - фокусное расстояние линзы; a - расстояние от предмета до линзы; b - расстояние от линзы до изображения) | 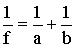 |
| Оптическая сила линзы |  |
| Оптическая сила двух совмещенных линз | 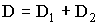 |
| Линейное увеличение линзы (y' - размер изображения предмета; y - размер предмета) | 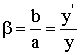 |
| Увеличение лупы (где L - линейный размер предмета) | 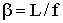 |
| Увеличение микроскопа (L - расстояние между задним фокусом объектива и передним фокусом окуляра, называемое оптической длиной тубуса; l - расстояние наилучшего зрения) | 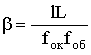 |
| Освещенность (φ - световой поток - средняя мощность энергии излучения; S - площадь освещаемой поверхности) | 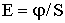 |
| Освещенность, создаваемая точечным источником света (I - сила света источника - световой поток, создаваемый точечным источником в единичном телесном угле; α - угол падения света на поверхность; r - расстояние от источника до поверхности) |  |
| Формула дифракционной решетки (d - период решетки; φ - угол наблюдения дифракционного максимума;k - номер дифракционного максимума; λ - длина волны света) |  |
| Постоянная дифракционной решетки (a,b - ширины темного и прозрачного промежутков дифракционной решетки; N - число штрихов решетки на единицу длины) | 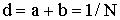 |
| Закон Брюстера - если угол падения света на границу раздела сред с относительным показателем преломления - n21, равен углу полной поляризации - α, то отраженный свет оказывается полностью поляризованным | 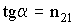 |
| Закон Стефана-Больцмана - полная лучеиспускательная способность абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры: σ = 5,67·-8ВТ/(м2·K4)- постоянная Стефана-Больцмана | 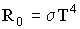 |
| Закон Вина - длина волны, соответствующая максимуму излучения абсолютно черного тела, обратно пропорциональна его абсолютной температуре: C'=2,9·10-3м·K - постоянная Вина | 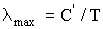 |
| Энергия кванта (закон Планка) h = 6,63·10-34Дж·с - постоянная Планка; ν, λ - частота и длина волны электромагнитного излучения; c =3·108м/с - скорость света в вакууме | 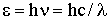 |
Формула Эйнштейна для фотоэффекта - энергия фотона ε = hν, поглощенная электроном, расходуется на совершение электроном работы выхода А из металла; оставшаяся часть этой энергии - кинетическая энергия фотоэлектрона .gif) |  |
| Красная граница (порог фотоэффекта) | 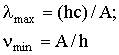 |
| Закон взаимосвязи массы и энергии | 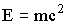 |
| Плотность потока излучения (E - энергия всех фотонов, падающих на поверхность) | 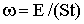 |
| Давление света ρ - коэффициент отражения света от поверхности | 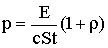 |
| Сериальная формула для атома водорода - частота электромагнитного излучения при переходе атома из стационарного состояния с (n) в стационарное состояние (k); R = 1,1·107м-1 - постоянная Ридберга. | 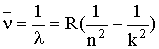 |
| Период полураспада - время за которое распадается половина всех радиоактивных ядер, λ - постоянная распада | 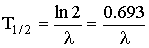 |
| Активность - количество распадов за одну секунду |  |
| Дефект массы ядра A - массовое число ядра, равно числу протонов и нейтронов в ядре; Z - зарядовое число ядра, равно числу протонов в ядре | 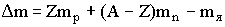 |
| Энергия связи ядра | 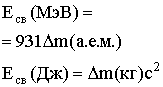 |
| Удельная энергия связи | 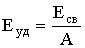 |
Примеры решения задачПример 9.На каком расстоянии друг от друга необходимо подвесить лампы в теплицах, чтобы освещенность Е на поверхности Земли в точке, лежащей посередине между двумя лампами была бы не менее 200 лк? Высота теплицы h = 2 м. Сила света каждой лампы I = 800 кд. Решение.
Расстояние l между лампами можно определить из формулы прямоугольного треугольника
Лампу можно принять за точечный источник света, так как ее размеры малы по сравнению с расстоянием до точки, в которой определяется освещенность. Поэтому определить расстояние r от лампы до точки A можно из формулы освещенности:
где α – угол, под которым падают лучи; Е – освещенность, создаваемая одной лампой, I – сила источника света.
Подставив в (2)
Подставим выражение (3) в (1) :
Вычисления:
Пример 10.Фокусное расстояние объектива микроскопа f1 = 5 мм, окуляра f2 = 25 мм. Предмет находится на расстоянии s = 5,1 мм от объектива (рис. 10). Вычислить длину тубуса микроскопа и даваемое микроскопом увеличение β. Решение. Увеличение микроскопа
где β1 – увеличение объектива; β1 – увеличение окуляра, определённые по формулам
где s‵ – расстояние от объектива до даваемого им действительного изображения; 0,25 – расстояние наилучшего видения для нормального глаза, м. С учетом (2) и (3) формула (1) примет вид
Расстояние s‵ от объектива до изображения можно найти из формулы линзы:
(s – расстояние от предмета до линзы), откуда
Подставив выражение для s‵ в (4), получим
Выпишем в СИ величины, входящие в расчетную формулу (5):
Длину тубуса определим, исходя из следующих соображений. Действительное изображение, даваемое объективом, должно лежать в фокусе окуляра, так как окуляр действует как лупа (рис.10). Поэтому длина тубуса
Вычисления:
Пример 11.Определить число штрихов на 1 мм дифракционной решётки, если при нормальном падении света длиной волны λ = 600 нм решетка дает первый максимум на расстоянии l = 3,3 см от центрального. Расстояние от решётки до экрана L = 110 см.
Число штрихов N на 1 мм решетки определим по формуле
Где d – период решётки (рис.11). Период решётки найдем из условия максимума:
где φ – угол, под которым наблюдается k – й максимум;k – порядок (номер) максимума. Ввиду того что для максимума 1 – го порядка угол мал, можно принять
Подставив в формулу (2) выражение синуса угла из (3), определим постоянную решетки:
С учетом (4) формула (1) примет вид
Выпишем числовые значения величин, входящих в (5), в СИ
Вычисления:
Пример 12.Определить концентрацию С сахарного раствора, если при прохождении света через трубку с этим растворам длиной l = 20 см плоскость поляризации света поворачивается па угол φ = 10º. Удельное вращение сахара в растворе 
Решение. Из формулы для угла поворота плоскости поляризации определим концентрацию раствора:
Выпишем числовые значения величии, входящих в (2) в СИ:
Вычислим искомую концентрацию:
Пример 13.Максимум энергии излучения абсолютно черного тела при некоторой температуре приходится на длину волн λм = 1 мкм. Вычислить излучательность тела при этой температуре иэнергию W, излучаемую с площади S = 300 см² поверхности тела за время t = 1 мин. Определить также массу, соответствующую этой энергии. Решение. Излучательность абсолютно черного тела определяется из закона Стефана-Больцмана:
где ς – постоянная Стефана—Больцмана; Т – термодинамическая температура тела. Из закона смещения Вина
определим термодинамическую температуру:
где λм – длина волны, на которую приходится максимум излучения при температуре T; С′ – постоянная Вина. Подставив выражение T из (2) в (1), получим
Энергию, излучаемую с площади S поверхности тела за время t, определим по формуле
По закону Эйнштейна взаимосвязи энергии и массы
(с – скорость света в вакууме,W – энергия) найдём массу излучения:
Проверим формулу (3):
Запишем в СИ величины, входящие в формулы (3), (4) и (6):
Вычислим искомые величины по формулам (3),(4) и (6):
Пример 14.Для предпосевного облучения семян применен лазер, излучающий электромагнитные волны длиной λ = 632 нм. Интенсивность излучения 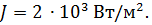 Определить число фотонов, поглощённых семенем, площадью S = 5 мм².
Время облучения 10 мин. Определить число фотонов, поглощённых семенем, площадью S = 5 мм².
Время облучения 10 мин.
Решение. Количество фотонов, поглощённых семенем, равно
Где W – энергия падающего света на семя, ε – энергия фотона. Энергия света, падающего на семя,
где J – интенсивность излучения, т. е. энергия света, падающего на 1 м² за 1 с; S – площадь; t – время. Энергия фотона определяется формулой Планка
где h – постоянная Планка, с – скорость света,λ – длина волны. Подставив (2) и (3) в (1), получим
Вычисления:
Пример 15.На поверхность площадью S = 3 см² за время t = 10 мин. падает свет, энергия которого W = 20 Дж. Определить: 1) облученность (энергетическую освещенность) поверхности, 2) световое давление на поверхность, если она: а) полностью поглощает лучи; полностью отражает лучи. Решение. Облученность определяется по формуле
Выпишем в СИ значения входящих в эту формулу величин: S = 3· 10-4 м²;
Вычисления:
2. Световое давление определяется по формуле
где
Если поверхность полностью отражает лучи, то ρ= 1 и тогда
Пример 16.Определить: 1) кинетическую энергию Т; 2) скорость и фотоэлектронов при облучении натрия светом длиной волны λ = 400 нм, если красная граница (порог) фотоэффекта для натрия λгр = 600 нм. Решение. 1. Кинетическую энергию фотоэлектронов определим из формулы Эйнштейна для фотоэффекта:
где h – постоянная Планка;ν – частота света; А – работа выхода электрона;
Частоту света определим по формуле
где с скорость света; λ — длина волны падающего света. Для поверхности металла, освещенной светом частотой νгр соответствующей красной границе фотоэффекта, кинетическая энергия фотоэлектронов равна нулю и формула (1) примет вид
Отсюда найдем работу выхода
где λгр – красная граница фотоэффекта, т.е. максимальная длина волны, при которой ещё возможен фотоэффект. Подставим в (2) выражение для ν из (3) и для А из (5):
Проверим формулу (6): Дж = Дж · с · м/с · 1/м = Дж. Выпишем числовые значения величин в СИ: h = 6,63 · 10-34 Дж·с; с = 3 · 108 м/с; λ = 4 · 10-7 м; λгр = 6·10-7 м. Вычисления:
(1 эВ=1,60·10-19Дж) один электрон-Вольт. 2. Из формулы
Учитывая, что m = 9,11 · 10-31 кг, вычислим искомую скорость фотоэлектронов:
Пример 17.Определить энергию фотона, излучаемого атомом водорода при переходе электрона с третьего энергетического уровня на первый, а также длину электромагнитной волны, соответствующую этому фотону. Решение. Переход электрона в атоме водорода с отдаленной орбиты на внутреннюю связан с излучением фотона (кванта энергии):
где ε - энергия фотона; h – постоянная Планка; с – скорость света в вакууме; ν, ε - частота и длина волны, соответствующие фотону с энергией ε. Длина волны излучаемого света связана с номером орбит соотношением:
где R – постоянная Ридберга; n – номер энергетического уровня, на который переходит электрон; k – номер энергетического уровня, с которого уходит электрон. Подставляем в (2) R = 1,1 · 107 м-1; n=1; k=3 и вычисляем длину волны λ:
В выражение (1) подставляем числовые значения h, c, ε и вычисляем ε:
Пример 18.Навеска почвы, в которую внесено удобрение с радиоактивны фосфором  , имеет активность А=10мкКи (микро Кюри).
Определить массу m радиоактивного фосфора в навеске. Период полураспада изотопа Т1/2=14,28 дня. , имеет активность А=10мкКи (микро Кюри).
Определить массу m радиоактивного фосфора в навеске. Период полураспада изотопа Т1/2=14,28 дня.
Решение. Массу радиоактивного вещества можно определить из формулы:
где N – число атомов (ядер); m/M – число молей; m – масса вещества; M – молярная масса вещества; NA – постоянная Авогадро. Из формулы (1) определим m:
Число атомов (ядер) связано с активностью А вещества:
где λ - постоянная распада, связана с периодом полураспада Т1/2 зависимостью:
Выразим величины, входящие в (5), в СИ: А = 10·3,7·104 Бк (Беккерелей); М = 32·10-3 кг/моль; NA = 6,02·1023 моль-1; Т1/2 = 14,28 дня·24 час·3600 с.
Пример 19.Определить дефект массы Δm и энергию связи Есв ядра атомов бора 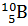 . .
Решение. Дефект массы ядра представляет собой разность массы нуклонов (протонов и нейтронов), составляющих ядро, и массы ядра и определяется по формуле
Где Z – зарядовое число (число протонов в ядре);(A-Z)-число нейтронов в ядре; mp – масса протона; A – массовое число (общее число нуклонов в ядре); mn – масса нейтрона; mя – масса ядра. Числа Z и А указываются при написании символа элемента: Z – слева внизу; А – слева вверху. В данном случае для бора Z=5, A=10. Массу ядра найдем по формуле
где mа – масса нейтрального атома; mе – масса электрона. Чтобы не вычислять каждый раз массу ядра, преобразуем формулу (1) с учетом (2):
Подставим числовые значения величин, входящих в (3), и вычислим дефекты массы ядра бора:
Энергия связи ядра – энергия, выделяющаяся при образовании ядра в виде электромагнитного излучения, определяется по формуле
где с – скорость света в вакууме. Если энергию связи Есв выражать в мегаэлектрон-вольтах, дефект массы ядра Δm в атомных единицах, то формула (4) принимает вид
где 931 – коэффициент, показывающий, какая энергия в мегаэлектрон-вольтах соответствует массе 1 а.е.м. Подставив значение Δm в (4), вычислим энергию связи:
Пример 20.Вычислить энергию ядерной реакции 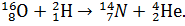 . Выделяется или поглощается энергия? . Выделяется или поглощается энергия?
Решение. Энергию ядерной реакции определяем по формуле
где Δm – изменение массы при реакции, т.е. разность между массой частиц, вступивших в реакцию, и массой частиц, образовавшихся в результате реакции:
Здесь
По формуле (2) вычисляем изменение массы при реакции Δm:
Подставляем числовое значение Δm в (1) и вычисляем энергию ядерной реакции:
В результате ядерной реакции выделяется энергия, так как масса исходных ядер больше массы ядер, образовавшихся в результате реакции.
|