|
Основы конструированияэлектронный учебно-методический комплекс |  | ||||||||||||||||||||||||
Назад | На главную | Содержание | Поиск на странице | Печать | E-mail | Далее | ||||||||||||||||||||||||||
7.4. Методы сборки Детали машин присоединении их в узлы и механизмы должны сохранять определённое взаимное расположение в пределах заданной точности. В одних случаях при сборке должен быть выдержан зазор, обеспечивающий взаимное перемещение деталей, в других - необходимый натяг, обеспечивающий прочность их соединения. В зависимости от вида производства применяют пять основных методов сборки:
Каждый из этих методов сборки обладает своими преимуществами и недостатками, и потому, в зависимости от характера производства, его организации, технической оснащённости и т. д., применяют тот или иной метод. Метод полной взаимозаменяемости предусматривает сборку машин без какой-либо дополнительной обработки деталей с установкой и заменой любой детали без пригонки. При сборке по этому методу требуется высокая точность изготовления деталей, специальное оборудование и оснастка. Метод полной взаимозаменяемости экономически целесообразен в массовом и крупносерийном производстве, где капитальные затраты на оснащение производства окупаются большим количеством изготовляемых машин. При этом методе благодаря отсутствию операций подбора или пригонки деталей ускоряется сборка машин, снижается трудоёмкость и увеличивается выпуск продукции. Помимо этого, использование комплектов запасных частей и узлов, изготовленных на основе полной взаимозаменяемости, обеспечивает быструю замену в эксплуатационных условиях изношенных или повреждённых деталей, что повышает эффективность эксплуатации машин.
Рисунок 7.2 - Схема размерной цепи узла вала
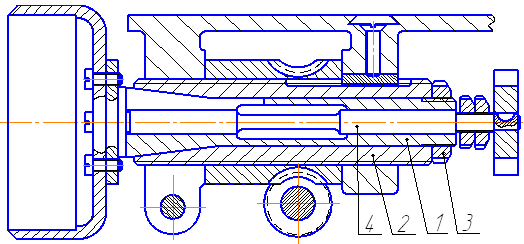
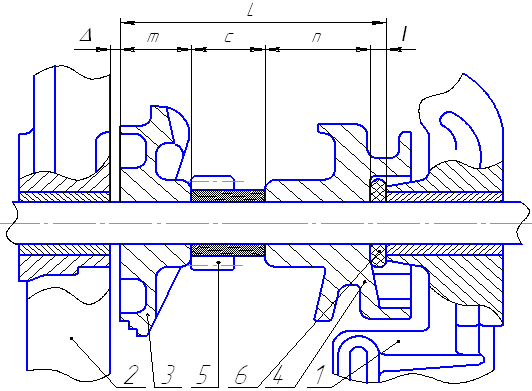
Рассмотрим пример сборки узла вала, при которой для обеспечения посадки эксцентриков 3 и 4 необходимо выдержать суммарный зазор (рисунок 7.2). Выделим размеры L, l, m, n, c, представленные на рисунке, в виде схемы размерной цепи. Допуск замыкающего звена (зазора r) определится по формуле: δΔ = δL + δl + δm + δn + δc . Решение этого уравнения является решением первой задачи определения допусков размерной цепи. Обозначим допуски на размеры, например следующим образом: δL = + 0,25; δl = - 0,1; δm = - 0,15; δn = - 0,1; δc = - 0,2, тогда δΔ = 0,25 + 0,1 + 0,15 + + 0,1 + 0,2 = 0,8 мм. Из решения этого уравнения видно, что все предельные отклонения размеров арифметически суммируются, то есть предполагается, что все детали, составляющие данный узел, выполнены с наименее выгодными предельными отклонениями. Например, все отверстия у подшипников - с предельно большими диаметрами, валы - с предельно малыми диаметрами, зубья зубчатых колёс - предельно тонкие, все отверстия для их осей - предельно раздвинуты или сужены и т. д. В действительности же, в результате действия ряда факторов, при изготовлении любой партии детали никогда не могут быть одинаковыми, то есть одни будут с размерами более близкими к номиналу, другие - с менее близкими. Вероятность сочетания одних крайних размеров в кинематических цепях с однородными по величине погрешностями (отклонениями от номинала) - крайне ничтожна. Так, например, в размерной цепи, имеющей элементы с одинаковыми величинами допусков, вероятность получить наихудшее сочетание крайних плюсовых или крайних минусовых отклонений при их распределении по закону равной вероятности весьма мала. При реальных распределениях вероятность сочетания крайних отклонений ничтожно мала. Решение о применении сборки с полной взаимозаменяемостью должно базироваться на анализе работы механизмов и на технико-экономических расчётах. При этом основными факторами, ограничивающими использование этого метода сборки, являются требования применения точных методов обработки большого количества деталей, сложных и точных приспособлений и контрольно-измерительных приборов, что нерентабельно при небольшом объёме производства и пр. Поэтому метод сборки механизмов и машин с применением полной взаимозаменяемости целесообразен и находит наибольшее применение в массовом и крупносерийном производствах. Метод сборки с применением сортировки деталей (метод группового подбора). Для осуществления высокой степени однородности посадок (без дополнительной пригонки деталей) и предотвращения увеличения затрат на производство при назначении излишне жёстких допусков сборку ведут путём подбора (предварительной сортировки деталей). Этот метод сборки применяют там, где по условиям работы деталей требуется зазор или натяг в более узких пределах, чем получаемый из основных размеров деталей с учётом допусков на их изготовление. В таком случае требуемые конструкцией зазор или натяг получают не за счёт изготовления деталей с минимальными допусками, а путём соответствующего подбора охватывающих и охватываемых деталей. То есть к отверстию с диаметром, близким к верхнему пределу, подбирают более полный вал и, наоборот, к отверстию с диаметром, близким к нижнему пределу, подбирают менее полный вал. Подбор деталей значительно упрощается, если детали обоих наименований по размерам (в пределах допусков на их изготовление) разбивают на несколько групп. Метод предварительной сортировки деталей на группы предусматривает разбивку полей допусков сопрягаемых деталей на несколько равных частей и подбора их таким образом, чтобы полномерные охватываемые детали сопрягались с полномерными охватывающими деталями.
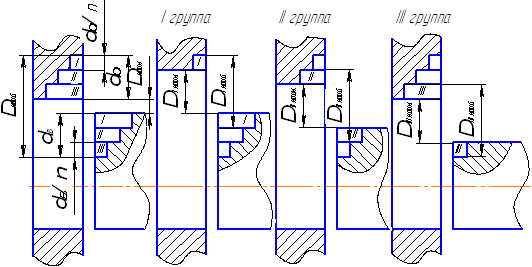
Рисунок 7.3 - Схема разбивки полей допусков сопрягаемых деталей на группы
Рассмотрим пример, когда сопрягаемые детали имеют различные допуски (рисунок 7.3). Тогда при сортировке деталей на число групп n=3 будем иметь для каждой группы допуск зазора: δΔ = (Δнаиб. - Δнаим.) / 3 = (δо - δв) / 3, где: δо - допуск на отверстие, δв - допуск на вал. При сборке методом предварительной сортировки (селективная сборка) детали сортируют таким образом, чтобы в каждую группу вошли охватывающие и охватываемые детали одной группы, то есть такие детали, у которых пределы отклонения лежат внутри этих полей допусков. Детали каждой из таких групп могут соединяться только между собой: охватывающие детали I группы - с охватываемыми деталями I группы, охватывающие детали II группы - с охватываемыми деталями II группы и т. д. Рассмотрим пример обработки пальца и поршня двигателя внутреннего сгорания. Палец по диаметру охватывается с допуском δв = 36- 0,012 , отверстие в поршне под палец обрабатывается с допуском δо = 36+ 0,015. При полных полях допусков получаем: Δнаиб. = 0,027 мм; Δнаим. = 0,000; δΔ = 0,027 мм. При сортировке этих деталей на три группы получаем допуск зазора: δΔ (n=3) = (δо + δв) / n = (0,015 + 0,012) / 3 = 0,009 мм. Разбивка деталей на группы приведена в таблице 14.
Таблица 1 - Разбивка диаметральных размеров пальцев и поршней (отверстий под пальцы) по группам
Описанный метод подбора деталей даёт возможность получать повышенную точность сборки. Однако применение его целесообразно лишь при сборке узлов с короткими размерными цепями и при обеспеченности сборки достаточным количеством деталей. Кроме возможности сортировать детали на группы внутри полей допусков, необходимо знать кривые распределения их размеров. Для этого нужно опытным путём получить кривые распределения и исследовать их, что позволит определить вероятность получения заданного зазора или натяга и одновременно установить количество деталей в каждой группе при сортировке. Если распределение размеров собираемых деталей (например, валы и втулки) подчиняется закону нормального распределения, то количество деталей каждой группы одинаково и сборка протекает нормально. Если же одна из деталей (например, втулка) подчиняется другому закону распределения, то, очевидно, некоторую часть деталей нельзя пустить в сборку из-за несоответствия в количественных соотношениях по группам. Тогда применяется статистический способ, заключающийся в том, что обследуется возможно большее количество операций, строятся для них кривые распределения и графо-аналитическим способом для каждой группы в отдельности устанавливается количество неиспользуемых деталей. Метод сборки с применением подбора деталей (неполная взаимозаменяемость). Этот метод основан на учёте вероятностей отклонения размеров, составляющих размерную цепь, причём возможно получение некоторого количества узлов, выходящих за установленные пределы точности. Сборка с применением подбора деталей, благодаря расширению допусков на все звенья размерной цепи, позволяет экономичнее изготовлять детали. Предполагая, что все отклонения размеров составляющих звеньев являются случайными и независимыми, подсчёт допуска замыкающего звена (зазора или натяга) производится по формуле:
В данном случае суммирование допусков производится не арифметически, а по правилу квадратного корня. Следовательно, чем больше допусков суммируется, тем больше становится разность между арифметической и квадратической суммами. Если рассеивание действительных размеров цепи подчиняется одной и той же закономерности - закону нормального распределения - и кривая совпадает значениями ± 3δ с границами допуска, то на основании теории вероятностей можно определить коэффициент сужения φх допуска зазора (или натяга) при переходе от полной к частичной взаимозаменяемости в зависимости от процента возможного получения узлов, выходящих за установленные пределы точности: φх = δΔх / δΔо , где δΔх характеризует повышенный допуск при х узлов. Ниже приведены значения коэффициента φх.
Таблица 2 - Значения коэффициента сужения допуска зазора φх в зависимости от процента узлов, выходящих за пределы точности
Взятый для примера (см. рисунок 12.2) допуск замыкающего звена (зазора Δ) при подборе определится: δΔх
= тогда коэффициент сужения допуска:
что по таблице соответствует примерно 18 % узлов, выходящих за установленные пределы точности. Таким образом, при переходе от полной к частичной взаимозаменяемости точность сборки повысилась в 2,1 раза (0,8 / 0,38). Однако при этом не исключена возможность выхода за установленные пределы точности около 18 % узлов, которые потребуют доделки. Метод сборки с применением компенсаторов. При большом числе звеньев размерной цепи и малом допуске замыкающего звена (зазора или натяга) необходимая для полной взаимозаменяемости точность изготовления деталей может в значительной степени усложнить производство и далеко выйти за пределы экономически целесообразной точности. В таких случаях приходится либо отказаться от полной взаимозаменяемости, допуская пригонку деталей по месту, либо вводить в конструкцию механизма тот или иной вид компенсатора, позволяющего регулировать в определённых пределах один из размеров. Такую регулировку называют компенсацией, а деталь, подбираемую в размерной цепи или специально вводимую в цепь для уменьшения допуска замыкающего звена, - компенсатором. Характерная особенность всех компенсаторов состоит в том, что сборка с их применением позволяет выдерживать установленные пределы точности в размерной цепи путём изменения величины одного из ранее намеченных звеньев. Обработка же всех остальных звеньев цепи осуществляется по допускам, наиболее приемлемым для данных производственных условий. Величину компенсирующего звена можно регулировать двумя способами: введением в размерную цепь специальной детали - прокладки, шайбы, промежуточного кольца и т. п. (неподвижные компенсаторы) и изменением положения одной из деталей, например, клина, втулки, эластичной или пружинной муфты, эксцентрика и т. п. (подвижные компенсаторы). Величину компенсации, то есть изменение компенсационного размера, которая должна перекрывать разницу между суммой принятых допусков для составляющих звеньев и допуском заданного звена, можно определить из уравнения:
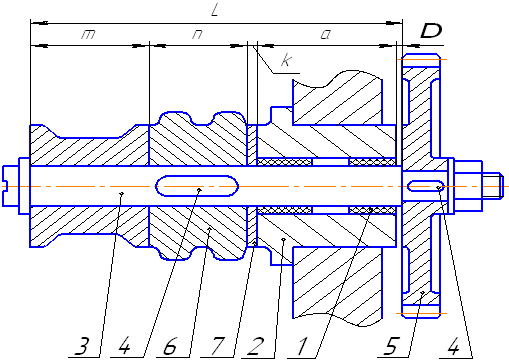
где: δк - величина компенсации; δi - величина расширенных допусков; m - общее количество звеньев размерной цепи, включая и замыкающее звено; δΔ - допуск зазора. Данное уравнение определяет границы наименьшего поля, в пределах которого должна быть обеспечена возможность изменения компенсационного размера. Если компенсатор позволяет изменять размер не непрерывно, а ступенями, например, сменные шайбы, прокладки, кольца и т. п.), то к наименьшему размеру компенсации нужно прибавить ещё и допуск на компенсатор. В качестве примера рассмотрим узел передачи, снабжённый компенсатором (рисунок 7.4). Во втулках 1 подшипника 2 вращается валик 3, на котором на шпонках 4 посажены зубчатое колесо 5 и шкив 6. Между торцами шкива и втулки помещено регулировочное кольцо 7 (компенсатор). Требуется определить количество размеров компенсатора, необходимых для обеспечения зазора, величина которого должна быть в установленных пределах Δ = 0,1 … 0,3 мм (δΔ = 0,2 мм).
Рисунок 7.4 - Схема узла передачи с компенсатором
Обозначим числовыми значениями составляющие размерной цепи с допусками: L=100+0,23; a=42-0,17; m=35-0,17; n=20-0,12; Δ=0,3-0,2; k=3-0,06 . Тогда наибольшая величина компенсации будет составлять: δк = (0,23 + 0,17 + 0,17 + 0,12 + 0,06) - 0,2 = 0,55 мм. При неподвижных компенсаторах расчёты необходимых количеств размеров определяют по формуле:
Тогда размеры компенсаторов, необходимых для обеспечения установленного зазора, определяются следующими величинами: К1 = 3,14-0,06 ; К2 = 3,28-0,06 ; К3 = 3,42-0,06 ; К4 = 3,56-0,06 . В качестве компенсатора очень часто используют набор нескольких одинаковых по толщине прокладок, одновременно вводимых в размерную цепь. Наименьшее количество прокладок определяется по формуле: n = δk / s , где s - толщина прокладок. Характерным примером подвижного компенсатора может служить компенсатор износа шпинделя (рисунок 7.5), представляющий собой разрезное кольцо 1 с конусом на одном конце и резьбой на другом. Кольцо помещается во втулке 2. При навинчивании на резьбу кольца 1 гайки 3 кольцо перемещается вправо и стягивается конусом втулки 2, вследствие чего радиальный зазор между шпинделем 4 и кольцом 1 устанавливается до заданного зазора.
Рисунок 7.5 - Схема установки подвижного компенсатора износа шпинделя
При наличии в размерной цепи звеньев, меняющихся по величине вследствие износа деталей, к величине компенсации необходимо прибавить величину ожидаемого износа, подлежащую компенсации после определённого срока работы машины путём периодического или непрерывного регулирования. Примерами периодически регулируемых компенсаторов могут служить конусные, клиновые, эксцентриковые, пружинные, резьбовые или шлицевые, зубчатые и другие компенсаторы. Метод сборки с индивидуальной пригонкой деталей по месту. Сборка с пригонкой деталей по месту заключается в том, что установленный предел точности замыкающего звена в размерной цепи достигается изменением величины одного из заранее намеченных звеньев путём снятия дополнительного слоя материала. По существу, сборка с доделкой деталей по месту является методом неполной взаимозаменяемости с пригонкой деталей в тех случаях, когда размер замыкающего звена лежит за пределами допускаемых отклонений. Чтобы производить пригонку за счёт выбранного компенсирующего звена, необходимо: - располагать поле допуска у подлежащей пригонке детали относительно номинала с таким расчётом, чтобы обеспечить на компенсирующем звене слой материала (припуск на пригонку), достаточный для компенсации величины превышения допускаемой погрешности замыкающего звена; - выдерживать при обработке деталей, входящих в размерную цепь, установленные, экономически приемлемые величины допусков; - не выбирать в качестве компенсирующего звено, которое является общим для нескольких размерных цепей, так как изменение его величины вносит погрешности во все связанные между собой размерные цепи. Существенными недостатками метода сборки с пригонкой по месту являются: - потребность в рабочих высокой квалификации; - повышенная трудоёмкость, достигающая иногда 40 … 50 % общей трудоёмкости сборки машины; - трудности учёта и нормирования пригоночных работ; - необходимость в большинстве случаев снятия стружки, что
вызывает загрязнение рабочих мест и требует дополнительной очистки и промывки
собранных узлов и механизмов.
| ||||||||||||||||||||||||||
© Красноярский государственный аграрный университет 2014
© Отдел информационных образовательных технологий 2014
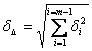 .
.
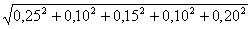 = 0,38 мм,
= 0,38 мм,
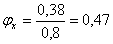 ,
,
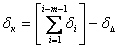 ,
,
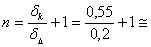 4.
4.