Если считать, что число рабочих дней в году 226, то ресурс рабочего времени рабочих в нашем случае составит 5×226×0,8= 904 машинодня. Здесь 0,8 – коэффициент использования рабочего времени (станки нуждаются в перенастройке, замене инструмента, смазке, профилактическом ремонте). Ресурс рабочего времени рабочих определяется аналогично, при условии, что коэффициент использования рабочего времени равен единице и в данном случае – 20×226×1=4520 человеко-дней. В клетках «цена единицы продукции» указана стоимость одного машинодня работы станков и одного человеко-дня работы рабочих. Прибыль от реализации единицы продукции первого вида составит 220 у.д.е., а от реализации единицы продукции второго вида составит 330 у.д.е. В соответствии с уже заключенным договором продукции вида А необходимо произвести не менее 10 единиц. Исследование рынка показало, что продукции вида Б можно реализовать в количестве не более 30 единиц. Прибыль от реализации единицы продукции вида А составит 220 у.д.е., от реализации единицы продукции вида В – 330 у.д.е. Необходимо определить количество продукции каждого вида, которое можно произвести при имеющихся запасах ресурсов с целью получения максимальной прибыли. В качестве элементов решения примем Х1 – количество продукции вида А; Х2 – количество продукции вида Б, которое необходимо выпустить при имеющихся запасах сырья для получения максимальной прибыли. В этом случае математическая модель будет иметь вид
Очевидно, что эта модель относится к классу задач линейного программирования (ЗЛП), а так как число неизвестных здесь равно двум, то она может быть решена не только аналитическим, но и графическим методом. 2. Графический метод решения задачи
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
(2.2.2) |
Линия уровня целевой функции перпендикулярна градиенту.
Графическое решение данной задачи приведено на рисунке 2.2.1.

Рисунок 2.2.1 – Графическое решение задачи
Область допустимых решений в данном случае образуется четырехугольником ОВСД. Ни одна точка внутри него или на его границе не противоречит ни одному из ограничений. Оптимальное решение находится в одной из вершин четырехугольника. Для нахождения оптимального решения перемещаем линию уровня целевой функции в направлении градиента до крайней точки ОДР. Такой точкой является точка С с координатами: Х1=16; Х2=8. Значение целевой функции F=40×16+30×8=880. Очевидно, что это решение не отличается высокой точностью, что характерно для графического метода.
Из рисунка видно, что ресурсы второго и третьего вида использованы полностью, а ресурс первого вида оказался в избытке. Для количественной оценки этого избытка определим сначала расход данного ресурса: 2×16+3×8=56. Запас равен 60, тогда остаток составит 60-56=4.
3. Графическое решение задачи с помощью Excel
Программа Microsoft Excel-2000 предназначена для работы с электронными таблицами, позволяющими собирать, анализировать и представлять количественную информацию в автоматическом режиме. Файл, создаваемый в Excel, называется рабочей книгой, которая состоит из рабочих листов. Рабочую книгу студент должен переименовать, ей понятное имя (например, Граф.мет1), и поместить в свою рабочую папку.
На рисунке 2.2.2 приведен пример организации исходных данных для решения графическим методом задачи (см. ф-лу (2.2.1)).

Рисунок 2.2.2 – Пример организации исходных данных
для графического решения задачи в Excel
Любое ограничение неравенство задачи линейного программирования в случае двух переменных строится по двум точкам. Например, ограничение по запасам сырья второго вида строится следующим образом. От неравенства переходим к равенству: 10Х1+5 Х2=200.
Задается любое значение одной переменной. (В данном случае Х1=0 занесено в ячейку В12 см. рис.2.2.3). Вторая координата этой точки вычисляется из уравнения:

Рисунок 2.2.3 – Ввод формулы для вычисления Х2
Эта формула введена в ячейку D12. Затем задается значение второй переменной. (Х2=0 занесено в ячейку D13 см. рис. 2.2.4). Вторая координата этой точки вычисляется из уравнения:
Эта формула введена в ячейку B13.

Рисунок 2.2.4 – Ввод формулы для вычисления Х1
После организации исходных данных необходимо выделить ячейки В10-J25 , щелкнуть «мастер диаграмм»
 и на первом шаге выбрать точечный вид диаграммы, а затем нажать «далее» (см. рис. 2.2.5).
и на первом шаге выбрать точечный вид диаграммы, а затем нажать «далее» (см. рис. 2.2.5).

Рисунок 2.2.5 – Выбор вида диаграммы
На втором шаге в подменю «Диапазон программирования» отметить, что ряды в столбцах (рис. 2.2.6), а в «Ряд» подписать имена рядов (см. рис. 2.2.7).

Рисунок 2.2.6 – Определение диапазона программирования

Рисунок 2.2.7 – Запись имен рядов
Третий и четвертый шаги можно пропустить. После нажатия на «готово» появляется график, пример которого приведен на рисунке 2.2.8.

Рисунок 2.2.8 – Пример графического решения задачи в Excel
Обычно, как и в данном примере, масштабирование оказывается настолько неудачным, что не видно не только оптимального решения, но и самой области допустимых решений. В этом случае необходимо навести курсор на ось Х, «щелкнуть» правой кнопкой мыши и установить целесообразные максимальные и минимальные значения, а так же цену делений. То же самой следует повторить и со шкалой У.
На рисунке 2.2.9 приведен пример графического решения со скорректированным масштабированием.
Оптимальное решение получается путем перемещения линии уровня целевой функции параллельно самой себе в направлении градиента до крайней точки области допустимых решений. В данном случае эта точка отмечена пунктирной линией.

Рисунок 2.2.9 – Пример графического решения задачи в Excel
4. Решение задачи линейного
программирования симплексным методом
Пусть имеется математическая модель, приведенная в п. 2 данного практического задания.
3Х1+2Х2≤60;
4Х1+20Х2≤200;
F=40Х1+30Х1→Мах.
Приведем эту задачу к канонической форме:
3Х1+2Х2+Х4=60;
4Х1+20Х2+Х5=200;
F-40Х1-30Х2=0.
Дополнительные переменные Х3, Х4 и Х5 равны разности между левой и правой частями ограничений и характеризуют недовыполнение данного ограничения (в данном случае – излишний запас).
Задача решается в стандартных симплексных таблицах. Исходная таблица заполняется коэффициентами исходной модели (табл. 2.2.2):
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | аio | aip |
|---|---|---|---|---|---|---|---|
| Х3 | 2 | 3 | 1 | 0 | 0 | 60 | 20 |
| Х4 | 3 | 2 | 0 | 1 | 0 | 60 | 30 |
| Х5 | 4 | 20 | 0 | 0 | 1 | 200 | 10 |
| F | -40 | -30 | 0 | 0 | 0 | 0 |
Базисными переменными являются переменные, входящие только в одно уравнение, с коэффициентом +1. Базисным переменным соответствует единичный вектор-столбец.
Решение читается следующим образом: базисные переменные равны свободным членам, а свободные переменные (переменные, не вошедшие в базис) равны нулю. Таким образом, в исходной симплексной таблице
Здесь значения переменных перечислены в порядке возрастания их индексов.
Это означает, что никакая продукция не выпускается (Х1 и Х2 равны нулю), остатки сырья равны их запасам (Х1=60, Х2=60, Х3=200). При этом будет получена прибыль равная нулю, что совершенно естественно.
В качестве разрешающего столбца выбирается любой столбец с отрицательной оценкой в строке целевой функции F. Выберем в качестве разрешающего, – второй столбец. Для всех его элементов вычисляем симплексные отношения аio/aiр (отношение элемента столбца свободных членов к соответствующему элементу разрешающего столбца) и записываем их в последний столбец таблицы. Разрешающий элемент определяется минимальным симплексным отношением (в таблице он выделен жирным шрифтом и курсивом).
На месте разрешающего элемента ставится 1, а остальные элементы данного столбца равны нулю.
Остальные столбцы, соответствующие базисным переменным остаются без изменения. Столбец, соответствующий выводимой из базиса переменной пересчитывается по общему правилу, описанному ниже. В данном случае Х2 вводится в базис вместо Х5 и столбец Х5 пересчитывается.
Элементы разрешающей строки делятся на разрешающий элемент.
Все остальные элементы таблицы пересчитываются по правилу прямоугольника. Пересчитываемый элемент с разрешающим элементом и соответствующими элементами разрешающей строки и столбца образует прямоугольник, изображенный на рисунке 2.2.10.

Рисунок 2.2.10 – Прямоугольник пересчета элементов симплексной таблицы
Пересчет производится по следующему правилу: произведение элементов главной диагонали, минус произведение элементов побочной диагонали, делим на разрешающий элемент. Это правило характеризуется формулой:
 |
(2.2.3) |
т.е. пересчитываемый элемент, умножается на разрешающий элемент, минус элемент соответствующего разрешающего столбца, умноженный на соответствующий элемент разрешающей строки, и эта разность делится на разрешающий элемент.
Например, пересчет элемента первого столбца первой строки:

Первая итерация расчета приведена в таблице 2.2.3.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | аio | aip |
|---|---|---|---|---|---|---|---|
| Х3 | 1,4 | 0 | 1 | 0 | -0,15 | 30 | 21,4 |
| Х4 | 2,6 | 0 | 0 | 1 | -0,10 | 40 | 15,4 |
| Х2 | 0,2 | 1 | 0 | 0 | 0,05 | 10 | 50 |
| F | -34 | 0 | 0 | 0 | 1,5 | 300 |
Как указывалось выше, решение задачи на любой итерации читается следующим образом: базисные переменные равны свободным членам (предпоследний столбец в таблице) а свободные переменные (те, которые не входят в базис) равны нулю. В данном случае
Или в краткой форме записи:
Здесь значения переменных приводятся в порядке возрастания их индексов.
Технико-экономический анализ полученного решения:
Выпускается десять единиц продукции второго вида (Х2=10). При этом ресурс первого вида останется в количестве тридцати единиц (Х3=30), ресурс второго вида останется в количестве сорока единиц (Х4=40), а ресурс третьего вида оказывается израсходованным полностью (Х5 свободная переменная, равна нулю).
Проверка полученного решения:
3×0+2×10+40=60;
4×0+20×10+0=200;
F=40×0+30×10=300.
Данное решение еще не является оптимальным, т.к. в строке целевой функции еще есть отрицательный элемент а1F=-3,4.
Вторая и все последующие итерации выполняются аналогично.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | аio | aip |
|---|---|---|---|---|---|---|---|
| Х3 | 0 | 0 | 1 | 0,54 | 0,1 | 8,5 | |
| Х1 | 1 | 0 | 0 | 0,38 | 0,04 | 15,4 | |
| Х2 | 0 | 1 | 0 | 0,74 | 0,17 | 6,9 | |
| F | 0 | 0 | 0 | 1,3 | 0,19 | 823 |
Это решение оптимально, т.к. в строке целевой функции нет отрицательных оценок.
Технико-экономический анализ полученного решения:
При имеющихся ресурсах следует выпустить 15,4 единицы (Х1=15,4) продукции первого вида и 6,9 единиц продукции второго вида (Х2=6,9). При этом ресурсы первого вида остаются в количестве 8,5 единиц (Х3=8,5), а ресурсы второго и третьего вида израсходованы полностью (Х4=Х5=0).
Проверка:
3×15,4+2×6,9+0=60;
4×15,4+20×6,9+0=200;
F=40×15,4+30×6,9=823.
Сравнение полученных результатов с результатами графического метода подтверждает, что графический метод при всей своей наглядности не отличается достаточной точностью.
5. Анализ решения с помощью
двойственного симплекс-метода
Симплексный метод позволяет получить оптимальное решение при имеющихся ресурсах, но не дает никаких рекомендаций об изменении запасов этих ресурсов с целью улучшения конечного результата. Эта проблема решается с помощью двойственного симплекс-метода.
Для перехода от прямой задачи к двойственной необходимо выполнить ряд операций. Матрица коэффициентов трансформируется. Правые части ограничений прямой задачи становятся коэффициентами целевой функции двойственной, а коэффициенты целевой функции прямой задачи становятся правыми частями ограничений двойственной. Знаки ограничений меняются на противоположные. Требование максимизации (минимизации) целевой функции меняется на требование ее минимизации (максимизации).
Таким образом, двойственная задача к той, что была рассмотрена в предыдущем разделе, будет иметь вид:
3У1+2У2+20У3≥30;
F'=60У1+60У2+200У3→Мin.
Решение двойственной задачи получается с учетом соответствия: прямым переменным прямой задачи соответствуют дополнительные переменные двойственной задачи, а дополнительным переменным соответствуют двойственные. В данном случае это соответствие выглядит следующим образом:

Решение двойственной задачи читается из последней симплексной таблицы следующим образом: двойственные оценки равны соответствующим оценкам в строке целевой функции. В данном случае У1=0; У2=1,3 и У3=0,28. Это означает, что первый ресурс находится в избытке и увеличение его запасов не приведет к увеличению прибыли. Второй и третий ресурс в дефиците, и увеличение их запасов на единицу позволит увеличить выпуск продукции. Причем, увеличение запасов второго вида сырья предпочтительнее.
6. Аналитический метод решения
с использованием программы Excel
В отличие от графического метода, аналитические методы (симплексные методы, метод Ньютона и др.) абсолютно точны. Кроме того, они дают возможность для точной количественной оценки излишков имеющихся ресурсов, дают еще и большие возможности для технико-экономического анализа полученного решения с целью выработки обоснованных рекомендаций по улучшению условий функционирования системы.
Рассмотрим решение задачи с помощью Excel на примере модели, построенной ранее (см. ф-лу (2.2.1)).

 |
Исходные данные организуются так, как это показано на рисунке 2.2.11.

Рисунок 2.2.11 – Пример организации исходных
данных задачи для решения ее в Excel
В ячейку Е7 записываем =СУММПРОИЗВ($B$5:$C$5;B7:C7). Здесь вычисляется значение целевой функции как сумма произведений фактического выпуска каждого вида продукции на прибыль от реализации ее единицы. Затем в ячейку Е10 записывается =СУММПРОИЗВ($B$5:$C$5;B10:C10). Здесь рассчитывается фактический расход каждого вида ресурсов, как сумма произведений норм расхода на фактический выпуск продукции каждого вида. Затем это копируется (растягивается) до ячейки Е15.
В ячейку I10 записываем =G10-E10 и копируем это до I15.
В ячейку J10 – =(G10-E10)/G10×100, до ячейки J15.
В ячейку С21 – =B21×G10, до С24;
В G21 – =F21×B21 до G24;
В К21 – =J21×B21 до К24;
В L10 – =G10-F21+J21.
После этого необходимо в меню выбрать «сервис» и «поиск решения». Затем необходимо заполнить появившуюся панель так, как это показано на рисунке 2.2.12, после чего дается команда «Выполнить» и «ОК».

Рисунок 2.2.12 – Ввод ограничений
В ячейках В5 и С5 появляется решение задачи – значения искомых переменных Х1 и Х2, а в Е7 – значение целевой функции. В ячейках I10-I15 – остатки ресурсов в единицах их измерения, а в J10-J15 – те же остатки в процентах от запасов.
После анализа остатков принимается решение о продаже наиболее избыточных из них. В данном примере продается 900 дней машинного времени, что записывается в ячейку F23. Точнее говоря, так как в данной задаче станки арендуются, то это означает сокращение срока аренды на 900 дней. При этом освобождается 18000 у.д.е. На эти деньги закупаем 600 единиц дефицитного сырья второго вида (18000/30=600).
В результате в ячейках L10-L13 появляются новые запасы, которые вручную записываются в ячейки G10-G15 для решения новой задачи с целью дальнейшей оптимизации запасов ресурсов.
7. Оптимизация запасов ресурсов в условиях
узкой специализации работы предприятия
Задача оптимизации производственной программы предприятия в простейшем случае имеет вид:

 |
(2.2.4) |
 |
(2.2.5) |
где cij – нормы расхода j-го вида ресурсов на производство единицы i-го вида продукции;
Cj – запасы ресурсов j-го вида;
n – количество видов продукции;
m – количество видов ресурсов;
F – целевая функция (прибыль);
pi – прибыль от реализации единицы i-го вида продукции.
Под ресурсами здесь следует понимать сырье, материалы, оборудование, трудовые ресурсы и пр.
Использование двойственного симплекс-метода показывает преимущества изменения одного ограничения по отношению с другими. В вышерассмотренной задаче двойственная оценка по второму ограничению оказалась выше, чем по третьему. Следовательно, увеличение запасов второго ресурса за счет реализации излишков первого позволит улучшить результаты решения в большей степени, чем увеличение запасов третьего ресурса.
Решение задачи оптимизации величины запасов ресурсов должно продолжаться путем реализации некоторой части ресурсов, приносящих меньшую прибыль с целью приобретения ресурсов более ценных с точки зрения целевой функции.
Увеличение запасов одного вида ресурсов за счет остальных в пределе приводит к выпуску только одного вида изделий, дающему наибольшую прибыль. Такая узкая специализация позволяет разработать самую простую типовую схему движения предметов труда, минимизировать внутрипроизводственные связи, уменьшить простои оборудование и пролеживание предметов труда, улучшить качество продукции и пр. В таком случае математическая модель задачи упрощается и принимает вид:

 |
(2.2.6) |
 |
(2.2.7) |
где r – номер наиболее рентабельной продукции;
Xr – количество наиболее рентабельной продукции;
Рk – прибыль от реализации этой продукции.
Эта задача состоит не только в определении объема выпуска продукции Xr, но и в определении величины запасов необходимых для этого ресурсов Ci.
С учетом того, что все запасы должны быть израсходованы полностью, они должны быть пропорциональны их нормам расхода. При изменении запаса одного ресурса соответствующим образом должны быть изменены и запасы других ресурсов, потребляемых при производстве программирования видов продукции. Запасы ресурсов естественно должны быть пропорциональны нормам их расхода:
 |
(2.2.8) |
 |
(2.2.9) |
Суммарная стоимость используемых ресурсов
 |
(2.2.10) |
где di – стоимость единицы ресурса i-го вида.
 |
(2.2.11) |
 |
(2.2.12) |
и по (2.2.6) необходимые для этого запасы ресурсов в пределах имеющихся финансовых возможностей.
В условиях острой конкурентной борьбы и с учетом возможного насыщения рынка такой подход далеко не всегда допустим, в связи с чем, в математическую модель приходится вводить соответствующие дополнительные ограничения вида:
 |
(2.2.13) |
 |
(2.2.14) |
где Xk;max – максимально возможный объем реализации k-го вида продукции;
Xg;min – минимально допустимый объем выпуска g-го вида продукции.
В первом случае Xk оказывается заданным. На производство этого вида продукции потребуются определенные деньги. Тогда задача сводится к определению количества второго по рентабельности вида продукции Хk2 по формуле
 |
(2.2.15) |
где  – затраты на предельно допустимый объем выпуска наиболее рентабельной продукции.
– затраты на предельно допустимый объем выпуска наиболее рентабельной продукции.
Если же в силу некоторых обстоятельств выпуск некоторого вида продукции ограничен снизу, то
 |
(2.2.16) |
где  – затраты на производство обязательной продукции.
– затраты на производство обязательной продукции.
Обобщая формулы (2.2.15) и (2.2.16) для любого числа ограничений сверху и снизу на выпуск продукции можно получить формулу, позволяющую определять объем наиболее рентабельной продукции из числа тех, на которые данные ограничения не распространяется
 |
(2.2.17) |
где m – количество видов продукции, на объем производства, которых наложены ограничения.
При этом запасы ресурсов должны вычисляться по формуле
 |
(2.2.18) |
Применение этих формул позволяет оптимизировать запасы ресурсов, свести к минимуму затраты, связанные с их хранением и обеспечивает выпуск наиболее рентабельной продукции при выполнении всех наложенных ограничений.
8. Пример решения задачи оптимизации запасов ресурсов
в условиях узкой специализации производства
| Наименование ресурса |
Запас ресурса |
Цена ресурса за единицу, у.д.е. |
Нормы расхода ресурса | |
|---|---|---|---|---|
| На 1 изделие вида А | На 1 изделие вида Б | |||
| Сырье С1 | 60 | 10 | 2 | 3 |
| Сырье С2 | 60 | 20 | 3/5 | 2 |
| Сырье С3 | 200 | 30 | 4 | 20 |
Прибыль от реализации единицы продукции вида А составляет 40 у.д.е., от реализации единицы продукции вида В – 30 у.д.е.
Математическая модель
3Х1+2Х2≤60;
4Х1+20Х2≤200;
F=40Х1+30Х2→Мах.
По исходным данным, приведенным в табл. 2.2.5, определим рентабельность производства обоих видов продукции
R2= 30/(3×10+2×20+20×30)×100=4,6%.
В результате принимается решение о производстве только первого вида продукции.
Суммарная стоимость используемых ресурсов:
С учетом (2.2.12) легко определяется Xr
 |
и по (6.6) необходимые для этого запасы ресурсов в пределах имеющихся финансовых возможностей:
При этом будет получена прибыль в размере
Таким образом, математическая модель задачи принимает вид:
3Х1+2Х2≤78;
4Х1+20Х2≤104;
Х1≥0; Х2≥0;
F=40Х1+30Х2→Мах.
Соответствующее этой модели графическое решение задачи приведено на рисунке 2.2.13.

Рисунок 2.2.13 – Графическое решение задачи
Оценка экономической эффективности решения задачи оптимизации
запасов в условиях узкой специализации производства
Экономическая эффективность определяется по той же формуле, которая использовалась ранее:
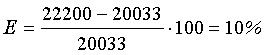 |
Таким образом, экономическая эффективность решения этой задачи составила 2167 у.д.е. или 10%
Узкая специализация производства более эффективна и в данном случае позволяет увеличить прибыль на
 |
9. Исходные данные задачи
формирования производственной программы
Данная задача может быть решена в двух вариантах – вручную с помощью симплексного метода или на компьютере с помощью Excel. В первом случае трудоемкость задачи оказывается значительно выше, поэтому размерность задачи может быть уменьшена. В любом случае в результате решения задачи требуется определить количество продукции каждого вида, которое необходимо произвести при имеющихся ресурсах для получения максимальной прибыли. Затем необходимо корректировать запасы ресурсов с целью их полного использования и получения большей прибыли. При этом необходимо сделать не менее трех итераций при ручном счете.
Определить экономическую эффективность решения задачи оптимизации запасов ресурсов.
Определить рентабельность производства обоих видов ресурсов.
Решить задачу оптимизации запасов ресурсов в условиях узкой специализации производства.
Определить экономическую эффективность узкой специализации производства.
Исходные данные задачи при
использовании симплексного метода
Исходные данные приведены в таблице 2.2.6.
| Наименование ресурса |
Запас ресурса |
Цена ресурса за единицу, у.д.е. |
Нормы расхода ресурса | |
|---|---|---|---|---|
| На 1 изделие вида А | На 1 изделие вида Б | |||
| Сырье С1 | 1050+10F | 20+10F | F/2 | - |
| Сырье С2 | 600+10E | 100+5F | F/5 | F/10 |
| Сырье С3 | 120+E+F | 50+(F+E) | - | E/10 |
Единица сырья С1 стоит 10 у.д.е., единица сырья С2 стоит 20 у.д.е., единица сырья С3 стоит 30 у.д.е.
От реализации единицы готовой продукции вида А получается прибыль 40 у.д.е., от реализации единицы готовой продукции вида В прибыль составит 30 у.д.е.
Исходные данные задачи
при использовании Excel
Планируется выпуск двух видов продукции А и Б. Для этого имеется сырье двух видов, запасы которых приведены в таблице 2.2.7. В аренду взято F станков и принято на работу 20 рабочих.
| Наименование ресурса |
Запас ресурса |
Цена ресурса за единицу, у.д.е. |
Нормы расхода ресурса на производство продукции вида | |
|---|---|---|---|---|
| А | Б | |||
| Сырье С1 | 190 | 20 | F | 8 |
| Сырье С2 | 200 | 30 | 10 | E |
| Станки | 180,8*F | 20 | 30+F | 20 |
| Труд. ресурсы | 4520 | 10 | 150 | 200+E |
Известны нормы расхода всех видов ресурсов на каждый вид продукции и цена единицы каждого вида ресурсов (см. табл. 2.2.1). Если считать, что число рабочих дней в году 226, то ресурс рабочего времени рабочих составит F×226×0,8=180,8×F машино-дней. Здесь 0,8 – коэффициент использования рабочего времени (станки нуждаются в перенастройке, замене инструмента, смазке, профилактическом ремонте). Ресурс рабочего времени рабочих определяется аналогично, при условии, что коэффициент использования рабочего времени равен единице и в данном случае – 20×226×1=4520 человеко-дней. В клетках «цена единицы продукции» указана стоимость одного машинодня работы станков и одного человеко-дня работы рабочих.
В соответствии с уже заключенным договором продукции вида А необходимо произвести не менее 10 единиц.
Исследование рынка показало, что продукции вида Б можно реализовать в количестве не более 30 единиц.
Прибыль от реализации единицы продукции вида А составит220 у.д.е., от реализации единицы продукции вида В – 330 у.д.е.
Необходимо определить количество продукции каждого вида, которое можно произвести при имеющихся запасах ресурсов с целью получения максимальной прибыли.
Задача решается итерационно до тех пор, пока остатки ресурсов не станут менее одного процента от их запасов, после чего определяется экономическая эффективность ее решения путем сравнения исходной и конечной экономической эффективности. Затем та же задача решается в условиях узкой специализации производства. Эта часть так же должна заканчиваться определением экономической эффективности.
2.2.2. Оптимизация запуска деталей в обработку
Без предварительной организации движения предметов труда по типовым технологическим маршрутам вообще невозможно планирование хода производства.
Отсутствие стандартизации технологических маршрутов изготовления предметов труда вызывает почти хаотическое их движение в производстве. Разработка типовой схемы движения предметов труда позволяет более чем в 10 раз сократить количество технологических маршрутов, при этом резко сокращается количество внутрипроизводственных связей и обеспечивается полная загрузка рабочих мест. Решению этих проблем способствует рационализация очередности запуска деталей в производство. В то же время, простое определение порядка запуска деталей в обработку еще не позволяет определить ни продолжительность цикла, ни простои оборудования, а, следовательно, не позволяет минимизировать последние. Определение и минимизация простоев оборудования особенно большое значение имеет при непоточном производстве.
При поточном же производстве час межоперационного пролеживания предметов труда наносит убытки во много раз большие, чем убытки производства от часа простоя рабочего места. Поэтому количественное определение величины пролеживания предметов труда способствует разработке типовой схемы движения предметов труда, обеспечивающей минимум затрат производственных ресурсов и позволяющей во много раз сократить количество технологических маршрутов, упрощающей планирование и управление производством.
Повышению упорядоченности движения предметов труда в производстве способствует рациональная очередность запуска деталей в производство. Упорядочивание порядка запуска деталей в производство может обеспечить либо сокращение длительности производственного цикла, либо уменьшение простоев рабочих мест.
1. Задача об одном станке
Рассмотрим вначале элементарную задачу об одном станке. Пусть на некотором оборудовании должны последовательно пройти обработку п деталей с различной длительностью, которая предполагается известной. Каким должен быть оптимальный порядок запуска деталей в обработку? Здесь и далее мы будем считать, что затрат на переналадку оборудования нет. Ясно, что общее время обработки всех п деталей будет одним и тем же при любой последовательности их запуска. Однако при этом окажется различным среднее время ожидания обработки для одной детали, а, следовательно, уменьшатся простои оборудования, ожидающего эти детали. Таким образом, среднее время ожидания в очереди разумно принять в качестве критерия оптимальности.
Решение здесь очевидно: запуск деталей должен производиться, начиная с той детали, для которой длительность обработки минимальна, в порядке возрастания этой величины.
2. Задача о двух станках. Алгоритм Джонсона
В этой задаче общее время производственного цикла уже зависит от порядка запуска деталей в обработку. Пусть имеется n деталей, каждая из которых должна последовательно пройти обработку сначала на первом, затем на втором станке. Предполагается заданным время tij обработки i-й детали на j-м станке (i=1,2,...,n; j=1,2). Требуется определить такой порядок запуска деталей, при котором общая длительность их обработки на обоих станках будет минимальной.
Эта задача решена С. Джонсоном. Им доказана оптимальность следующего правила. Вначале детали, подлежащие обработке, условно делят на две группы. В первую группу относят детали, для которых ti1≤ti2, т.е. те, время обработки которых на первом станке не превышает времени обработки на втором станке. Остальные детали образуют вторую группу. Вначале следует обрабатывать детали первой группы в порядке возрастания длительности их обработки на первом станке. Затем должны обрабатываться детали второй группы в порядке убывания времени их обработки на втором станке.
Для большего числа станков задача аналитического решения не имеет.
3. Обобщения алгоритма Джонсона
и рекомендации по составлению расписания
Значительно больший практический интерес представляло бы решение задачи, подобной задаче о двух станках, для произвольного количества m станков, на которых должны последовательно пройти обработку п деталей. Анализируя алгоритм Джонсона для задачи о двух станках, можно извлечь из него рекомендации, применимые и к общему случаю последовательной обработки деталей на п танках при произвольном m.
Обобщения алгоритма Джонсона
- В обработку сначала запускают детали, требующие минимальное время обработки на первом станке в порядке возрастания этого времени.
- В обработку запускаются сначала детали, требующие максимальное время обработки на последнем станке в порядке убывания этого времени.
- В обработку запускаются сначала детали, у которых “узкое место” находится дальше от начала процесса обработки (“узким местом” для данной детали называется станок, на котором обработка этой деталей занимает наибольшее время).
- Обрабатываются вначале детали, у которых суммарное время обработки на всех станках максимальное в порядке убывания этого времени.
Каждое из вышеописанных обобщений алгоритма Джонсона в определенных условиях имеет свои преимущества и свои недостатки. Каждое из этих правил в определенной степени логично. Применение первого из них способствует скорейшему вовлечению в обработку второго станка. Второе правило позволяет уменьшить конечный простой первого станка. Третье правило способствует наиболее быстрому "проскакиванию" к концу технологической линии тех деталей, для которых обработка на первом станке занимает меньшее время, с тем, чтобы освободить первый станок деталям, для которых он является узким местом. К сожалению, эти правила не совместимы друг с другом: последовательность обработки, найденная с использованием одного из них, не соответствует последовательности, полученной по другим правилам.
Пятый метод решения этой задачи основан на усреднении результатов решения задачи по четырем известным рекомендациям. Рассмотрим следующий пример обработки 8 деталей на 5 станках. Исходные данные приведены в таблице 2.2.8.
| Станок | Время обработки, мин | |||||||
|---|---|---|---|---|---|---|---|---|
| деталь | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 2 | 5 | 3 | 7 | 9 | 4 | 1 | 8 |
| 2 | 10 | 1 | 5 | 7 | 3 | 8 | 2 | 9 |
| 3 | 5 | 8 | 10 | 4 | 1 | 3 | 9 | 2 |
| 4 | 7 | 5 | 2 | 4 | 10 | 1 | 8 | 6 |
| 5 | 1 | 10 | 3 | 5 | 7 | 4 | 2 | 11 |
| Суммарное время обработки | 25 | 29 | 23 | 27 | 30 | 20 | 22 | 36 |
В результате решения задачи по четырем выше указанным рекомендациям получаем такой порядок запуска деталей в обработку:
– по первой рекомендации: 7-1-3-6-2-4-8-5;
– по второй рекомендации: 2-8-5-4-6-3-7-1;
– по третьей рекомендации: 2-8-5-7-3-1-6-4;
– по четвертой рекомендации: 8-5-2-4-1-3-7-6.
Примечание. Если по какой-либо рекомендации две, или больше деталей оказываются равноценными, то для определения их приоритетов следует воспользоваться какой-либо другой рекомендацией. Например, по рекомендациям вторая и восьмая детали равноценны, но по первой рекомендации целесообразно в обработку запустить сначала вторую деталь, т.к. время ее обработки на первом станке меньше, чем у восьмой детали.
Для каждой детали найдем сумму мест во всех полученных решениях:
первая деталь: (2 + 8 + 6 + 5) = 21;
вторая деталь: (5 + 1 + 1 + 3) = 10;
третья деталь: (3 + 6 + 5 + 6) = 20;
четвертая деталь: (6 + 4 + 8 + 4) = 22;
пятая деталь: (8 + 3 + 3 + 2) = 16;
шестая деталь: (4 + 5 + 7 + 8) = 24;
седьмая деталь: (1 + 7 + 4 + 7) = 19;
восьмая деталь: (7 + 2 + 2 + 1) = 12.
Расположим детали в порядке возрастания суммы мест:
Это и является новым решением.
При решении конкретных задач для трех и более станков рекомендуется проанализировать результаты, полученные по каждому из этих правил, и в качестве окончательного варианта выбрать ту последовательность, которая обеспечивает минимум суммарного времени обработки. Для этого необходимо построить графики Ганта.
4. Построение графиков Ганта
Пусть две детали должны пройти последовательную обработку на трех станках. Исходные данные примера приведены в таблице 2.2.9.
| Номер станка | Время обработки детали | |
|---|---|---|
| 1 | 2 | |
| 1 | 4 | 4 |
| 2 | 9 | 5 |
| 3 | 3 | 6 |
Построение графика Ганта иллюстрируется рисунком 2.2.14 (рисунок повернут).

Рисунок 2.2.14 – График Ганта
Производственный цикл начинается с того, что первая деталь обрабатывается на первом станке четыре минуты, а затем передается на второй станок, где обрабатывается девять минут.
Как только освобождается первый станок, на него поступает вторая деталь и обрабатывается здесь четыре минуты, однако, так как второй станок еще занят, – она ждет своей очереди в течение пяти минут. Это называется пролеживанием предмета труда.
После завершения обработки второй детали на втором станке, она передается на третий станок, а на освободившийся второй станок поступает первая деталь. Здесь она обрабатывается в течение пяти минут, а так как третий станок освободился на две минуты раньше, то происходит его простой, равный двум минутам.
5. Оптимизация работы оборудования
путем концентрации его микропростоев
Оперативное определение неизбежных простоев рабочих мест позволяет организовывать последовательно-параллельную работу оборудования, концентрируя микропростои отдельных станков в начале их работы. Такие резервы могут быть использованы для загрузки станков работами, связанными с изготовлением других деталей. Это позволит существенно повысить общую производительность всего производственного участка.
На рисунке 2.2.15 приведен пример графика Ганта для трех станков, на которых производится последовательная обработка четырех деталей.

Рисунок 2.2.15 – График Ганта для четырех деталей и трех станков
На рисунке каждая деталь изображена определенной линией.
Для концентрации микропростоев оборудования следует использовать следующий алгоритм:
- Начало и окончание обработки последней детали на всех станках остается прежним;
- На i-том станке окончание обработки j-1-детали равно началу обработки этой детали на i-1 станке, причем, i = n,...,2, т. е. процесс корректировки графика Ганта начинается с последнего рабочего места.
На основании этого алгоритма на рисунке 2.2.16 построен график Ганта со сконцентрированными микропростоями.

Рисунок 2.2.16 – График Ганта со сконцентрированными микропростоями
В то же время следует отметить, что концентрация микропростоев не всегда гарантирует в конечном итоге их полное отсутствие на всех рабочих местах, что иллюстрируется рисунком 2.2.17.

Рисунок 2.2.17 – График Ганта с неизбежными простоями
Проведем сравнительный анализ графика Ганта, приведенного на рисунке 2.2.16, и графика Ганта со сконцентрированными микропростоями, приведенного на рисунке 2.2.17.
| Станок | Деталь | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 10 | 3 | 4 | 0 |
| 3 | 14 | 0 | 5 | 2 |
Продолжительность работы первого станка (для рисунка 2.2.1.):

Второго станка:

Третьего станка:

Теперь определим продолжительность работы каждого станка со сконцентрированными микропростоями.



Сравним продолжительности циклов соответствующих станков до концентрации микропростоев и после нее:

Таким образом, продолжительность работы первого станка не меняется, а, начиная со второго станка, появляется возможность повышения производительности на каждом рабочем месте. В данном случае продолжительность работы второго станка и третьего станка можно сократить на 7 минут, т.е., производительность второго станка может быть увеличена на 18,9%, а для третьего станка на 17,1%.
6. Исходные данные задачи оптимизации
порядка запуска деталей в обработку
Исходные данные приведены в таблице 2.2.11
| Станок | Деталь | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| 1 | F | 1 | 6 | E+4 |
| 2 | 10 | F+2 | E | 5 |
| 3 | 2 | E+2 | F+4 | 8 |
| 4 | E | 9 | 8 | F |
Необходимо построить график Ганта для исходного порядка запуска деталей в обработку, т.е. в последовательности 1-2-3-4-5. Затем следует составить пять решений задачи по обобщениям алгоритма Джонсона; для каждого решения построить график Ганта; для одного из решений сконцентрировать микропростои оборудования к концу производственного цикла; вычислить суммарные простои и длительность работы каждого станка в исходном графике Ганта и после концентрации микропростоев, сравнить полученные результаты и сделать выводы.
Задача завершается определением экономической эффективности наилучшего из решений по сравнению с исходным порядком запуска деталей. Экономическая эффективность определяется путем сравнения длительностей производственного цикла.
2.2.3. Задачи сетевого планирования комплекса работ
Многие организационные и технические мероприятия представляют собой сложную совокупность взаимосвязанных работ. Примерами таких мероприятий могут быть строительство и реконструкция цехов и любых других объектов, освоение новой техники и технологии, производство проектно-конструкторских работ и пр. При реализации таких проектов возникает ряд проблем: определение рациональных сроков начала и окончания той или иной работы, обеспечивающих выполнение всего мероприятия за минимальное время; распределение ресурсов между работами, минимизирующее суммарные затраты. В частности, отдельные работы могут оказаться “узким местом”, сдерживать проведение остальных мероприятий. Их следует выявить и выполнять заблаговременно или выделить на них дополнительные средства.
Сетевой график позволяет получить наглядное представление о порядке выполнения отдельных операций, а так же о взаимосвязях между ними. Он является моделью реализации мероприятия, на которой можно изучать последствия тех или иных решений с целью выбора наилучшей стратегии управления.
На сетевом графике каждая работа изображается стрелкой, а факт ее окончания, называемый событием, обозначается кружком (рис.2.2.18).

Рисунок 2.2.18 – Изображение работы и факта ее окончания на сетевом графике
Предположим теперь, что некоторая работа а2 может начаться только после окончания работы а1. В таком случае говорят, что работа а2 опирается на работу а1 (рис. 2.2.19)

Рисунок 2.2.19 – Работа а2 опирается на работу а1
Если же одна работа опирается на несколько других, то естественно, что она может начаться не ранее, чем закончится последняя из предшествующих. Логическая же связь со всеми остальными изображается в виде фиктивных работ, не требующих затрат времени и изображаемых пунктирными стрелками, идущими к началу данной работы. На рисунке 2.2.20 работа а4 опирается на а1, а2 и а3, но позже всех заканчивается а2.

Рисунок 2.2.20 – Фрагмент сетевого графика с фиктивными работами
При построении сетевых графиков наиболее распространенными являются следующие ошибки:
- Висячие вершины свидетельствуют о том, что соответствующие им работы в принципе не нужны. Соответствующий этому случаю фрагмент сетевого графика приведен на рис. 2.2.21.

Рисунок 2.2.21 – Фрагмент сетевого графика с “висячей вершиной”
- Замкнутый цикл (зацикливание) свидетельствует о том, что комплекс работ в принципе не может быть выполнен. Соответствующий этому случаю фрагмент сетевого графика приведен на рис. 2.2.22.

Рисунок 2.2.22 – Фрагмент сетевого графика с “замкнутым циклом”
1. Пример решения задачи сетевого
планирования комплекса работ
Построение сетевого графика начинается с простого перечисления всех необходимых работ (таблица 2.2.12).
| Наименование работы |
Обозначение работы |
Опирается на работу |
Ранг работы |
Новая нумерация |
|---|---|---|---|---|
| Монтаж крана | b1 | b3, b6 | 3 | a5 |
| Закладка фундамента | b2 | b4, b5, b6 | 3 | a6 |
| Завоз оборудования | b3 | b5 | 2 | a3 |
| Завоз материалов | b4 | b5 | 2 | a4 |
| Расчистка территории | b5 | - | 1 | a1 |
| Разметка | b6 | b5 | 2 | a2 |
| Возведение стен | b7 | b1, b2, b4 | 4 | a7 |
| Монтаж перекрытия | b8 | b7 | 5 | a8 |
| Электротехнические работы | b9 | b8 | 6 | a9 |
| Сантехнические работы | b10 | b8 | 6 | a10 |
| Приемосдаточные испытания | b11 | b8, b9, b10 | 7 | a11 |
Затем на основании простого логического анализа заполняется второй столбец таблицы и определяется ранг каждой работы. Работы первого ранга не опираются на другие. Работы второго ранга опираются только на работы первого ранга. Работы третьего ранга могут опираться на работы второго и первого ранга и т.д.
После этого производится перенумерация работ и заполняется последний столбец таблицы. При этом безразлично, в каком порядке присваивать номера работам одного и того же ранга.
После этого составляется новая таблица, в которой указывается продолжительность выполнения каждой работы (таблица 6.13).
| Наименование работы | Обозначение работы | Опирается на работу | Продолжительность работы |
|---|---|---|---|
| Расчистка территории | a1 | - | 6 |
| Разметка | a2 | a1- | 2 |
| Завоз оборудования | a3 | a1 | 4 |
| Завоз материалов | a4 | a1 | 2 |
| Монтаж крана | a5 | a2, a3 | 5 |
| Закладка фундамента | a6 | a2, a4 | 3 |
| Возведение стен | a7 | a4, a5, a6 | 7 |
| Монтаж перекрытия | a8 | a7 | 6 |
| Электротехнические работы | a9 | a8 | 3 |
| Сантехнические работы | a10 | a8 | 5 |
| Приемосдаточные испытания | a11 | a9, a10 | 6 |
Существует несколько методов решения задач сетевого планирования. По-видимому, наиболее наглядным и простым является графоаналитический метод. При этом методе сначала проводится ось времени. В начале оси располагается исходный узел 0. Величина стрелки и угол ее наклона для любой работы выбираются таким образом, чтобы ее проекция на ось времени была равна ее продолжительности. Очевидно, что в этом случае есть множество вариантов изображения каждой работы. Например, на рисунке 2.2.23 приведено три варианта изображения одной и той же работы.

Рисунок 2.2.23 – Варианты изображения одной и той же работы
Если же одна работа опирается на несколько других, то изображающая ее стрелка должна начинаться из самого правого кружка, а логическая связь с другими работами изображается пунктирными стрелками (фиктивные работы). Пример этого случая приведен на рисунке 2.2.24.

Рисунок 2.2.24 – Фрагмент временного сетевого графика с фиктивными работами
Сетевой график, построенный на основании исходных данных программирования таблицы 2.2.12, приведен на рисунке 2.2.25.

Рисунок 2.2.25 – Сетевой график комплекса работ,
построенный графоаналитическим методом
На графике двойными стрелками выделены критические работы. Критическая дуга составляется только из сплошных стрелок. Из графика, построенного графоаналитическим методом сразу видна общая продолжительность производственного процесса. В данном случае Тобщ=42 дня.
Фиктивные работы характеризуют резервы времени соответствующих реальных работ. Эти резервы определяются проекцией соответствующей фиктивной работы на ось времени. В данном случае работа а2 имеет резерв времени в два дня, а4 – восемь дней, а9 – один день.
Знание этих резервов позволяет изменить сроки начала некритических работ и дать рекомендации о перераспределении имеющихся ресурсов в пользу критических работ с целью сокращения общей продолжительности выполнения всего комплекса.
Например, завоз оборудования можно осуществить не сразу после завершения работы а1, а на 8 дней позже (см. рис. 2.2.25). При этом не будет излишне загромождаться территория, и само оборудование будет более сохранным.
Если же, некоторые некритические работы выполняются за счет трудовых ресурсов, то вполне можно снять с них часть рабочих и перевести их на выполнение критических работ.
Задачам сетевого планирования характерны все свойства задач динамического программирования:
- задача может быть разбита на этапы (по времени, в пространстве, этапы производственного процесса и пр.);
- аддитивность решения – результат решения всей задачи может быть получен в результате суммирования результатов решения на каждом отдельном этапе;
- регрессивность решения – решение разворачивается от конца к началу.
На рисунке 2.2.26 показано решение той же задачи методом динамического программирования.

Рисунок 2.2.26 – Решение задачи сетевого планирования
методом динамического программирования
Вначале безо всяких масштабов строится сетевой график. Для определения продолжительности выполнения всего комплекса работ, в соответствии с принципами динамического программирования, процесс решения разворачивается от конца к началу.
В конечное состояние 11 система может перейти из состояния 10. Для этого потребуется 6 дней (а11=6).
В состояние 10 система может перейти из состояния 6, 9 и 8. Максимальное время этого перехода составляет 5 дней (работа а10). 9-10 и 6-10 – фиктивные работы, не требующие затрат времени, поэтому над кружками 9 и 10 ставим предыдущее число 6.
В состояние 8 система может перейти по дуге а2-а8, а3-а7, а4-а7, а3-а5 и а4-а5. Длины этих дуг (в днях) составляют, соответственно, – 20, 11, 9, 15 и 13 дней. Наибольшей продолжительности требует переход системы из 2 в 8, а все остальные состояния соединяем с 8 фиктивными работами (пунктирными стрелками). Аналогичным образом доходим до начала производственного процесса.
Окончательный результат, естественно, получается точно таким же, как и при использовании графоаналитического метода.
Использование различных методов при решении одной и той же задачи позволяет исключить возможность появления даже случайной ошибки и широко используется в научных исследованиях и в проектной практике.
2. Исходные данные сетевого планирования комплекса работ
Исходные данные задачи сетевого планирования приведены в таблице 2.2.14.
| Наименование работы | Обозначение работы | Опирается на работу | Продолжительность работы |
|---|---|---|---|
| Монтаж крана | b1 | b3, b6 | E |
| Закладка фундамента | b2 | b4, b5, b6 | F+3 |
| Завоз оборудования | b3 | b5 | 3 |
| Завоз материалов | b4 | b5 | 4 |
| Расчистка территории | b5 | - | F |
| Разметка | b6 | b5 | 2 |
| Возведение стен | b7 | b1, b2, b4 | F+E+5 |
| Монтаж перекрытия | b8 | b7 | F+E |
| Электротехнические работы | b9 | b8 | 5 |
| Сантехнические работы | b10 | b8 | 8 |
| Приемосдаточные испытания | b11 | b8, b9, b10 | 4 |
Задачу необходимо решить графоаналитическим методом и методом динамического программирования, проанализировать резервы времени некритических работ и дать качественные рекомендации о перераспределении ресурсов между критическими и некритическими работами с целью сокращения общей продолжительности выполнения всего комплекса работ.
2.2.4. Задача о реконструкции предприятия
Пусть имеется мебельное предприятие, выпускающее пять видов мебели. В связи с изменениями конъюнктуры рынка и новейшими достижениями техники и технологии необходимо реконструировать предприятие и полностью изменить ассортимент. Необходимо без остановки производства реконструировать все три цеха и постепенно изменить ассортимент продукции. Данная задача может быть решена методом динамического программирования.
1. Метод динамического программирования
Метод динамического программирования универсален. С его помощью можно решать такие задачи, как нижеприведенная задача управления запасами, задача прокладки оптимального пути, оптимизации траектории взлета самолета, задача о реконструкции, задача о замене оборудования и пр.
К задачам динамического программирования относятся задачи, обладающие следующими свойствами:
- задача может быть разбита на этапы (по времени, в пространстве, этапы технологического производства, реконструкции, строительства и пр.);
- аддитивность решения и аддитивность критерия оптимальности, т.е. решение всей задачи получается путем суммирования результатов решения задач на отдельный этапах, а значение критерия оптимальности всей задачи получается путем суммирования значений частных критериев оптимальности на отдельных этапах;
- регрессивность решения – процесс решения разворачивается от конца к началу.
В динамическом программировании процесс решения задачи рассматривается как процесс принятия управляющих решений, причем, этот процесс рассматривается от конца к началу.
В общем случае задача динамического программирования может быть сформулирована следующим образом. Имеется некоторая экономическая система, находящаяся в начальный момент времени Т0 в состоянии S0 Это состояние определяется n-мерным вектором параметров системы в заданный начальный момент времени. Такими параметрами могут быть сочетания показателей производственно-хозяйственной деятельности предприятия: объем реализуемой продукции, прибыль, производительность труда, стоимость основных производственных фондов, ассортимент выпускаемой продукции и пр.
В соответствии с планом развития за период времени Tk-Tj система должна быть переведена в некоторое конечное состояние Sk, определяемое соответствующими значениями составляющих вектора состояний в момент времени Tk. Переход может быть обеспечен за конечное число шагов, на каждом из которых система переводится в некоторое промежуточное состояние Si. При этом необходимо обеспечить оптимум критерия, обеспечивающего качество управления.
Перевод системы из состояния в состояние характеризуется набором последовательных состояний S0, S1, …, Si, …, Sk. и называется траекторией системы. Этот перевод из состояния в состояние обеспечивается посредством ряда последовательных управляющих воздействий или управлений, которые будем обозначать через wi.
Совокупность управлений wi обозначим через W. Тогда можно сказать, что задача динамического программирования заключается в выборе оптимального управления W последовательно переводящего систему из состояния в состояние, начиная из S0 в состояние Sk, при условии, что критерий оптимальности F(W) принимает экстремальное значение.
2. Пример решения задачи о реконструкции
методом динамического программирования
На рисунке 2.2.27 приведены исходные данные задачи, где в кружках обозначены номера состояния системы, между кружками – курсивом затраты на переходы системы из одного состояния в другое. В частности, – над горизонтальными линиями – затраты на внедрение нового изделия, а справа от вертикальных линий – затраты на реконструкцию соответствующего цеха в условных денежных единицах (у.д.е).

Рисунок 2.2.27 – Исходные данные примера задачи о реконструкции
Как указывалось выше, процесс решения разворачиваем от конца к началу. В конечное состояние 24 система может перейти из состояния 22 или 23. Иначе говоря, реконструкция может завершаться или внедрением пятого изделия, или реконструкцией третьего цеха. Для этого потребуется соответственно 11 и 14. Эти числа ставим над соответствующими кружками (см. рис. 2.2.28) и линии заменяем на стрелки.

Рисунок 2.2.28 – Первые два шага решения
На следующем шаге – переход системы из состояния 20 в конечное состояние, возникает два альтернативных варианта: или переход по пути 20-22-24 или по пути 20-23-24. Иначе говоря, реконструкция может завершаться или реконструкцией третьего цеха, а затем – внедрением пятого изделия, или наоборот,- сначала внедрением этого изделия, а затем реконструкцией цеха. В первом случае для этого понадобится 11+15=26 у.д.е, а во втором 14+13=27. Очевидно, что первый вариант выгоднее, поэтому стрелку ставим вверх и над кружком 20 ставим минимальное число 26 так как это показано на рисунке 2.2.29. Такое решение называется условно оптимальным.

Рисунок 2.2.29 – Третий шаг расчета
Следующие шаги выглядят следующим образом (см. рис. 2.2.30)

Рисунок 2.2.30 – Следующие шаги решения задачи
В дальнейшем процесс решения разворачивается аналогично от конца к началу равномерно по диагонали по всей площади схемы.
На последнем шаге расчета получается безусловно оптимальное решение, которое определяется траекторией непрерывных стрелок (см. рисунок 2.2.31). В данном случае эта траектория определяет следующую стратегию реконструкции всего предприятия: реконструкция первого цеха, замена первого изделия, реконструкция второго цеха, замена второго изделия, реконструкция третьего цеха, замена остальных изделий.
На рисунке внутри кружков для компактности рисунка указаны уже не номера состояний системы, а суммарные затраты на реконструкцию. В первом кружке – минимально возможные затраты на всю реконструкцию.

Рисунок 2.2.31 – Окончательное решение задачи
о реконструкции мебельного предприятия
|
|