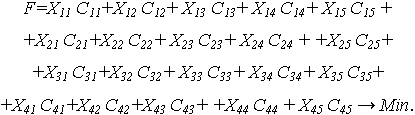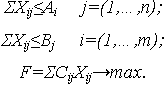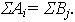МОДУЛЬ 2. Виды логистики
ТЕМА 2.5. Транспортная логистика

ПРАКТИЧЕСКОЕ ЗАДАНИЕ

Значительная часть логистических операций на пути движения материального потока от первичного источника сырья до конечного потребителя осуществляется с применением различных транспортных средств. Затраты на транспортные операции составляют до 50% от суммы затрат на логистические операции.

Транспортная логистика решает проблемы обеспечения технической и технологической сопряженности участников транспортного процесса, согласования их экономических интересов.

К задачам транспортной логистики относят:

• создание транспортных систем;
• обеспечение технологического единства транспортно-складского процесса;
• совместное планирование транспортного процесса с производственным и со складским;
• определение рациональных маршрутов доставки и пр.

2.5.1. Постановка транспортной задачи и построение ее математической модели

2.5.2. Построение исходного опорного плана

1. Метод северо-западного угла

2. Метод наименьшего элемента

2.5.3. Оптимизация опорного решения

1. Метод оценки циклов

2. Метод потенциалов

2.5.4. Транспортные задачи с дополнительными ограничениями

1. Задачи с обязательными поставками

2. Задачи с запретами

3. Задача с ограниченной пропускной способностью

4. Транспортная задача с вырожденным решением

2.5.5. Задачи, приводимые к транспортной

1. Задача о реконструкции

2. Задача о назначениях

2.5.6. Решение транспортной задачи с использованием Excel

2.5.7. Исходные данные транспортной задачи

2.5.8. Составление кольцевых маршрутов. Задача коммивояжера

1. Пример решения задачи составления кольцевых маршрутов

2. Исходные данные задачи оптимизации кольцевого маршрута

2.5.9. Задача оптимизации прокладки дороги

1. Пример решения задачи оптимизации прокладки дороги

2. Данные задачи оптимизации прокладки дороги

2.5.10. Определение оптимального срока замены транспортного средства

1. Пример решения задачи замены транспортного средства

2. Исходные данные задачи определения момента замены транспортного средства

2.5.1. Постановка транспортной задачи
и построение ее математической модели

Пусть имеется n поставщиков однородной продукции (присвоим им имена – a_i) и m потребителей этой продукции (b_j). Каждый поставщик может поставлять свою продукцию любому из потребителей. Известны затраты C_ij на перевозку единицы продукции от каждого поставщика к каждому потребителю. Необходимо так распределить перевозки, чтобы суммарные затраты были минимальными. Элементы решения – Х_ij количество продукции, перевозимой от каждого поставщика к каждому потребителю.

Структурная схема данной задачи в сетевой постановке приведена на рис. 2.5.1.

Рисунок 2.5.1 – Пример структурной схемы транспортной задачи

Обозначим через A_i возможности поставщиков и через B_j потребности потребителей.

Составим математическую модель задачи.

Ограничения по производственным мощностям поставщиков:

(2.5.1)

Ограничения по производственным мощностям потребителей:

(2.5.2)

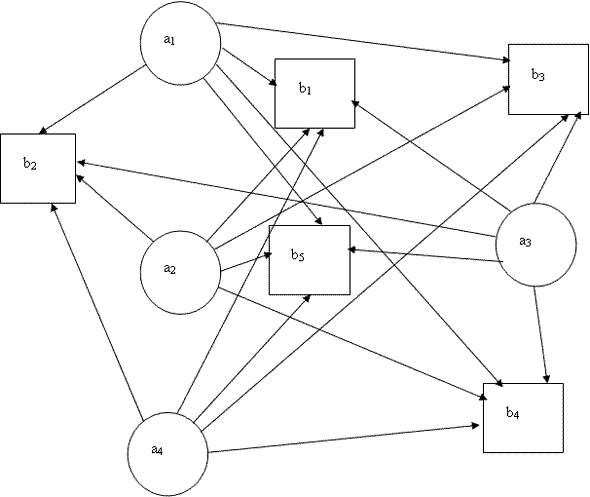
Целевая функция – требование минимизации суммарных затрат на перевозки:

(2.5.3)

В краткой форме записи эта модель имеет вид:

(2.5.4)

Закрытой моделью транспортной задачи называется такая задача, в которой суммарные потребности потребителей равны суммарным возможностям поставщиков, т.е.

(2.5.5)

2.5.2. Построение исходного опорного плана

Опорный план является основой для оптимизации процесса. Существует несколько способов его построения. Здесь описано два из них. Один из них – метод северо-западного угла – наиболее простой, но и наименее эффективен, второй – метод наименьшего элемента несколько сложнее, но значительно ближе к оптимальному.

1. Метод северо-западного угла

Существует несколько методов составления исходного опорного плана. Самый простой из них – метод «северо-западного угла». Исходные данные примера (затраты на перевозку единицы продукции от каждого поставщики к каждому потребителю) приведены в верхних правых углах таблицы 2.5.1.

Таблица 2.5.1

Метод наименьшего элемента состоит в заполнении клеток, начиная с тех, в которых стоят наименьшие затраты на перевозку (см. табл. 2.5.1). В данном случае минимальную стоимость имеют перевозки по каналу А₄-В₂ – 8 у.д.е. Ставим в эту клетку максимально возможное количество перевозок – 175 (т.к. возможности А₄=175). Следующие по затратам на перевозку каналы А₄-В₅ и А₄-В₄. Однако, возможности А₄ уже исчерпаны, поэтому далее заполняется клетка, соответствующая каналу А₂-В₄, в которую ставим 152 единицы груза (А₂=152). Далее заполняем клетку А₂-В₂. Сюда можно поставить только 25, т.к. второму потребителю требуется 200, а 175 он уже получает от А₄.

Следующие по затратам перевозки по каналу А₂-В₄ – 11 у.д.е. В эту клетку можно поставить только 127 единиц продукции, т.к. А₂=152, а он уже поставил 25 единиц потребителю В₂.

Канал А₂-В₅ и А₃-В₂ не рассматриваем, т.к. возможности А₂ уже исчерпаны, а потребности В₂ полностью удовлетворены. Поэтому затем заполняется клетка, соответствующая каналу А₃-В₃ (затраты на перевозку – 42 у.д.е.)

В дальнейшем транспортная таблица заполняется аналогично.

2. Метод наименьшего элемента

Исходные данные примера приведены в верхних правых углах таблицы 2.5.2.

Таблица 2.5.2

Заполнение таблицы начинается с клетки, соответствующей минимальной стоимости перевозок. Такой клеткой в данном случае является канал А₄-В₂. Поставим сюда 175 единиц, т.к. А₄=175.

Следующая по затратам клетка соответствует каналу А₂-В₂. По этому каналу можно перевезти 152 единицы продукции, однако, потребитель В₂ уже получил от А₄ 175 единиц и ему необходимо еще только 25 единиц (200-175=25).

Следующая по затратам клетка А₂-В₄. Здесь можно осуществить поставки в объеме 152 единиц, но поставщик А₂ уже поставляет потребителю В₂ 25 единиц и у него остается только 127, что и ставится в клетку А₂-В₄.

В дальнейшем таблица заполняется аналогично.

2.5.3. Оптимизация опорного решения

1. Метод оценки циклов

Метод состоит в том, что для каждой свободной клетки составляется и оценивается цикл. Цикл, это прямоугольная фигура, в которой все клетки, кроме первой, заняты. Наиболее типичные примеры циклов приведены на рисунке. 2.5.2.

Рисунок 2.5.2 – Примеры циклов транспортных перестановок

В таблице 2.5.3 приведены циклы для исходной задачи, представленной в таблице 2.5.1. В пустой клетке ставим минус, а далее по порядку плюс, минус, плюс, минус и т.д.

Таблица 2.5.3

Составление и оценка циклов для оптимизации плана перевозок

Оценки циклов:

	- +72-22+16-40=+26;
	- +25-22+16-52=-33;
	- +40-22+16-52+12-11=-17;
	- +15-70+22-8=-41;
	- +10-8+16-40=-22;
	- +4-8+16-52=-40;
	- +15-11+12-52+16-8=-28;
	- +27-70+22-16=-37;
	- +52-52+12-11=+1;
	- +55-70+22-16+52-12=31;
	- +8-16+52-12=+32;
	- +52-40+52-12=+52.

Перестановки осуществляются по циклу с наибольшей по модулю отрицательной оценкой. В данном случае это цикл, составленный для клетки А₂-В₄, имеющий оценку минус 40. По циклу переставляется минимальное число, стоящее в отрицательной вершине. Здесь в отрицательных вершинах стоят 154 и 127 единиц товаров. Переставляем 127, путем вычитания этого числа из отрицательных вершин и прибавления в положительные.

В результате получается новый план, приведенный в таблице 2.5.4.

Таблица 2.5.4

Для этого плана снова составляются и оцениваются все циклы, Процедура повторяется до тех пор, пока есть отрицательные циклы.

После каждой итерации вычисляется целевая функция – суммарные затраты на перевозку. В данном случае

При использовании данного метода для наглядности каждый цикл рекомендуется обозначать своим цветом.

2. Метод потенциалов

Каждому поставщику поставим в соответствие некоторый потенциал α_i, а каждому потребителю – потенциал β_j (см. таблицу 2.5.5.).

Таблица 2.5.5

Оптимизация плана перевозок методом потенциалов

Присвоим любому потенциалу произвольное значение, например α₃=0. Остальные потенциалы легко определяются из условия, что для любой занятой клетки

Для каждой свободной клетки вычислим псевдостоимость

Запишем псевдостоимость в левых нижних уголках свободных клеток, а разность в кружках. Сравнивая эти разности с результатами, полученными в предыдущем разделе, убеждаемся, что эти разности характеризуют оценки соответствующих циклов.

Для клетки с наибольшей по модулю отрицательной разностью составляется единственный цикл, по которому и производится перестановка.

Перестановки могут осуществляться и сразу по нескольким циклам, но только в том случае, если они охватывают разные клетки.

По циклам, как и ранее, переставляется минимальное количество грузов, стоящее в отрицательных клетках.

Процедура повторяется до тех пор, пока есть отрицательные циклы.

2.5.4. Транспортные задачи
с дополнительными ограничениями

1. Задачи с обязательными поставками

В качестве примера решения такой задачи рассмотрим исходные данные, приведенные в таблице 2.5.6.

Таблица 2.5.6

Пусть, в силу определенных обстоятельств (например, госзаказ), третий поставщик А₃, несмотря на фактические затраты, обязан поставить четвертому потребителю В₄ не менее 100 единиц продукции. Исключим эту обязательную поставку из транспортной таблицы (см. таблицу 2.5.7).

Таблица 2.5.7

Затем решается обычная транспортная задача, но при определении суммарных затрат на перевозки необходимо учесть и затраты на обязательные поставки: 100×52=5200.

2. Задачи с запретами

В ряде случаев поставки по некоторым каналам оказываются недопустимыми. Это, например, могут быть условия технологии (предприятии, производящее продукцию на экспорт не может потреблять сырье низкого качества), отсутствие у потребителя подходящей взлетно-посадочной полосы для приема воздушных транспортных средств и пр. Исходная транспортная таблица задачи с запретами, составленная методом наименьшего элемента, приведена в таблице 2.5.8.

Таблица 2.5.8

Пусть в силу некоторых обстоятельств поставки по каналу А₁-В₂ невозможны. Поставим в соответствующую клетку транспортной таблицы вместо реальной стоимости перевозки М (сколь угодно большое число, большее любого наперед заданного числа). Решаем эта задачу методом потенциалов, так как это было показано в разделе 2.5.3.2 (см. таблицу 2.5.9).

Таблица 2.5.9

Решение транспортной задачи (первая итерация)

Наибольшая по модулю разность между стоимостью и псевдостоимостью (оценка цикла) соответствует клетке А₂-В₂, для которой и составляем цикл. После перестановки по этому циклу 75 единиц продукции (минимальное число, стоящее в отрицательной вершине) получается новый план, представленный в таблице 2.5.10.

Таблица 2.5.10

Решение транспортной задачи (вторая итерация)

Как видно из таблицы, объем перевозок по каналу с запретом уменьшился. Повторяем процедуры метода потенциалов. В результате получаем новую таблицу 2.5.11.

Таблица 2.5.11

В дальнейшем процесс решения происходит аналогично до тех пор, пока есть отрицательные оценки циклов.

3. Задача с ограниченной пропускной способностью

Пусть в исходной задаче, приведенной в таблице 2.5.12, в силу некоторых обстоятельств по каналу А₃-В₄, несмотря на низкую стоимость перевозок, можно поставить не более 125 единиц продукции.

Таблица 2.5.12

Представим поставщика А₃ в виде двух поставщиков – А₃¹ и А₃², находящихся в одном и том же месте. Производственные мощности этих поставщиков соответственно 100 (ограничение на поставку) и 125 единиц. Естественно, что затраты на перевозки и них останутся такими же, как и у А₃, однако, для выполнения поставленного ограничения у поставщика А₃¹ по каналу А₃¹-В₄ поставим запрет М (см. табл. 2.5.13).

Таблица 2.5.13

Таким образом, получается обычная задача с запретами. Результаты решения этой задачи приведены в таблице 2.5.14.

Таблица 2.5.14

Как видно из таблицы 2.5.14, третий поставщик будет поставлять четвертому потребителю не более 125 единиц продукции, а оставшиеся 100 ед. он поставит потребителю А₁.

4. Транспортная задача с вырожденным решением

Число занятых клеток в транспортной таблице должно быть равно n+m-1, где n – число поставщиков, m – число потребителей. В противном случае решение вырожденное (таблица 2.5.15).

Таблица 2.5.15

В данном случае занято всего 7 клеток, в то время как должно быть занято 4+5-1=8 клеток. Следовательно, план является вырожденным.

Для приведения задачи к закрытому виду поставим в одну свободную клетку базисный ноль. Пусть такой клеткой является А₁-В₅. Однако в этом случае в ряде циклов с отрицательными оценками он окажется в отрицательной вершине. В качестве примера в таблице 2.5.16 приведен цикл, имеющий оценку

Таблица 2.5.16

Транспортная таблица, приведенная к невырожденному
решению с неправильным расположением базисного нуля

Очевидно, что в этом цикле можно переставлять только ноль, что не имеет никакого смысла. Поэтому базисный ноль целесообразно ставить в клетку с минимальной стоимостью перевозок. Поставим его в клетку А₂-В₄ (см. таблицу 2.5.17).

Таблица 2.5.17

Транспортная таблица, приведенная к невырожденному
решению с правильным расположением базисного нуля

Наибольшую по модулю отрицательную оценку имеет цикл, начинающийся с клетки А₄-В₂ (-47). Здесь базисный ноль стоит в положительной вершине цикла и по этому циклу можно переставлять 25 единиц продукции.

2.5.5. Задачи, приводимые к транспортной

Целый ряд задач, никак не касающихся транспортных перевозок, могут быть решены по вышеописанному алгоритму решения транспортных задач. К таким задачам относятся рассмотренные ниже задача о реконструкции и задача о назначениях, или задача выбора.

1. 7.5.1 Задача о реконструкции

Весь прогресс развития человечества основан на дисбалансе между возможностями и потребностями. Пусть, например, имеется два поставщика и четыре потребителя однородной продукции. Исходные данные задачи приведены в таблице 2.5.18.

Таблица 2.5.18

Производственные мощности поставщиков А₁+А₂=200+135=335. Потребности потребителей – 120+120+150+150=540. Таким образом, для удовлетворения потребностей потребителей производственные мощности поставщиков необходимо увеличить на 205 единиц. Для этого можно или реконструировать второе предприятие и увеличить его мощность до 340 ед. или построить новое предприятие мощностью 205 ед. В этом случае таблица исходных данных задачи принимает вид 2.5.19

Таблица 2.5.19

В таком случае, т.к. запасы поставщиков больше, чем потребности потребителей (ΣА_i≥ΣВ_j), задача превращается в задачу открытого типа. Для приведения ее к закрытому типу вводим фиктивного потребителя, потребности которого равны разности между реальными возможностями поставщиков и потребностями потребителей:

Так как фактически этого потребителя нет, то и затраты на перевозку продукции до него равны нулю, что и отражено в таблице 2.5.20. По каналам же А₁-В_ф и А₂-В_ф ставим запреты (стоимость перевозок – М). В противном случае могло бы оказаться, что необходимо уменьшить мощность А₁, что, очевидно, совершенно нецелесообразно или уменьшить мощность А₂ при одновременной его реконструкции и увеличении мощности, что совершенно бессмысленно.

Таблица 2.5.20

Исходный опорный план составляем методом наименьшего элемента (таблица 2.5.21).

Таблица 2.5.21

В соответствии с этим планом А₁ будет поставлять свою продукцию В₂ и В₃; А₂ – В₁ и В₂; второго поставщика следует реконструировать и увеличить его мощность на 55+150=205, а строить новое предприятие нецелесообразно, т.к. А_н будет поставлять свою продукцию несуществующему фиктивному потребителю.

В результате решения задачи выше описными методами получаются результаты, представленные в таблице 2.5.22.

Таблица 2.5.22

Из таблицы следует, что целесообразно реконструировать второе предприятие и увеличить его мощность на 70+15=80 и построить новое предприятие мощностью 120.

2. Задача о назначениях

Содержательная постановка задачи о назначениях: Имеется n, бригад, которые должны выполнить комплекс работ на n объектах. Известны затраты времени t_ij на выполнения каждой бригадой работ на каждом объекте. Каждая бригада должна работать только на одном объекте и на каждом объекте может работать только одна бригада. Необходимо так распределить бригады между объектами, чтобы суммарное время выполнения всех работ было минимальным. Кроме того в данной задаче кроме минимизации времени выполнения всех работ повышается ответственность каждого работника за качество выполнения работы и облегчается выявление «бракоделов».

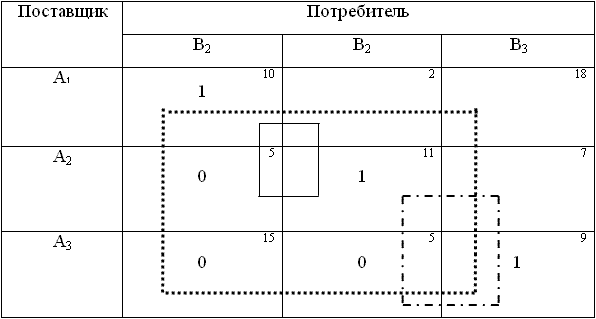
Рассмотрим решение этой задачи на примере, исходные данные которого приведены в таблице 2.5.23. Здесь в правых верхних углах каждой клетки указаны соответствующие затраты времени t_ij.

Таблица 2.5.23

В данной задаче применяются элементы алгебры логики. Элементы решения X_ij – факт выполнения работ i-ой бригадой на j-ом объекте. Этот факт может быть истинным, что обозначается единицей, или ложным – ноль.

Математическая модель задачи:

• Каждая бригада работает только на одном объекте –

(2.5.6)

• На каждом объекте работает только одна бригада –

(2.5.7)

• Целевая функция –

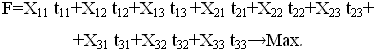(2.5.8)

В общем случае в краткой форме записи эта модель выглядит следующим образом:

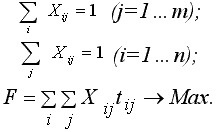(2.5.9)

Рассмотрим пример решения задачи о назначениях.

Таблица 2.5.24

Число занятых клеток должно быть 3+3-1=5, а занято только три клетки. Поэтому для каждой свободной клетки приходится искать свое положение базисного нуля, который должен находиться в положительной вершине цикла. Пример решения приведен в таблице 2.5.25.

Таблица 2.5.25

Пример решения задачи о назначениях методом оценки циклов

2.5.6. Решение транспортной задачи с использованием Excel

Использование программы Excel существенно облегчает процесс решения задачи.

Как показано на рисунке 2.5.3, в ячейки D3-F7 заносятся затраты на перевозку единицы груза от каждого поставщика к каждому потребителю. Запреты на перевозки по соответствующим каналам гарантируются введением значительно большей по сравнению с остальными стоимости (в данном случае – 1000).

Потребности потребителей вводятся в ячейки D10-F10. Запасы поставщиков – в В13-В17.

В ячейках С13-С17 насчитываются суммарные перевозки каждого поставщика, а в G15-G17 – разницы между этими перевозками и фактическими запасами поставщиков. Эти разности должны быть равны нулю.

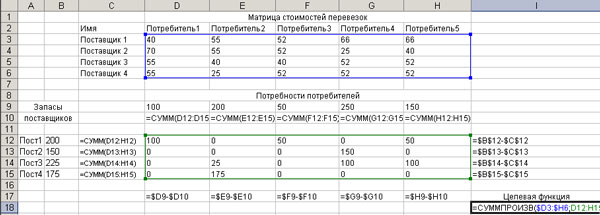
Рисунок 2.5.3 – Пример организации исходных данных
транспортной задачи для использования Excel

В ячейках D11-F11 вычисляется суммарное количество грузов, получаемое каждым потребителем, а в D19-F19 – разности между потребностями и фактическим получением грузов. Эти разности так же должны быть равны нулю.

Целевая функция – суммарные затраты на перевозки определяются произведениями фактических перевозок на соответствующие затраты, что записывается в ячейку G20.

После введения исходных данных следует нажать «сервис», «поиск решения» и заполнить открывшиеся окна, так как это показано на рис. 2.5.4.

Рисунок 2.5.4 – Поиск решения транспортной задачи

Здесь в окне «ограничения» в первой строке записываются тривиальные ограничения – требования неотрицательности искомых переменных.

Во второй строке – требование точного удовлетворения потребностей потребителей.

В третьей строке – требование полного исчерпания запасов поставщиков.

Пример окончательного решения задачи приведен на рис. 2.5.5.

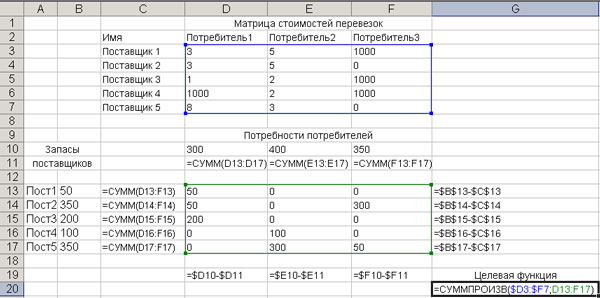
Рисунок 2.5.5 – Пример окончательного решения транспортной задачи

2.5.7. Исходные данные транспортной задачи

Имеется три пункта поставки однородного груза a₁, a₂ и a₃ и три пункта потребления этого груза B₁, B₂ и B₃. Запасы груза у поставщиков: A₁, A₂ и А₃, соответственно. Потребности потребителей: B₁, B₂ и B₃. Суммарная мощность поставщиков оказывается недостаточной, поэтому принято решение об ее увеличении, причем имеется два альтернативных варианта: 1 – реконструкция первого предприятия поставщика, 2 – строительство нового предприятия. Известна стоимость перевозки 1 т груза c_ij из i-го пункта поставки в j-й пункт потребления. Кроме того, имеется дополнительное ограничения – второй поставщик А₂ может поставить первому потребителю B₁ ограниченное количество груза. Необходимо при имеющихся ограничениях так распределить перевозки между поставщиками и потребителями, чтобы суммарные транспортные расходы были минимальны (см. таблицу 2.5.26).

Таблица 2.5.26

Необходимо составить математическую модель задачи с учетом дополнительного ограничения; найти первоначальный опорный план производства и организации перевозок методом наименьшего элемента; оптимизировать план производства и организации перевозок методом потенциалов или методом оценки циклов; сделать технико-экономическое истолкование найденного оптимального решения; определить экономическую эффективность решения задачи оптимизации перевозок.

2.5.8. Составление кольцевых маршрутов.
Задача коммивояжера

Многие потребители заказывают со складов партии «меньше чем вагон», «меньше чем трейлер», что значительно увеличивает издержки, связные с доставкой таких грузов. Для сокращения транспортных расходов склад может организовать объединение небольших партий грузов для нескольких клиентов, до полной загрузки транспортных средств. Маршрут от склада до нескольких потребителей с возвратом на склад называется кольцевым маршрутом.

Одной из основных проблем, решаемых транспортной логистикой, является оптимизация маршрутов движения транспортных средств. Эта проблема справедлива и для оптимизации кольцевых маршрутов (последовательность посещения заказчиков) и может быть решена с помощью задачи коммивояжера.

1. Пример решения задачи составления кольцевых маршрутов

Имеется сеть магазинов, снабжаемых из одного распределительного склада. Снабжение производится автомобилями грузоподъемностью 5 т. Средние величины заказов магазинов приведены в таблице 2.5.27.

Таблица 2.5.27

Задача решается с помощью алгоритма Свира или алгоритма дворника-стеклоочистителя.

Зададим положение магазинов в полярной системе координат. Полюс системы – точку 0, разместим в месте расположения распределительного склада (см. рис.7.6).

Выберем первоначальное, нулевое, положение полярной оси φ=0. Положение потребителя определяется расстоянием от центра и углом φ, который образован полярной осью и направленным на потребителя. Суть алгоритма Свира заключается в том, что полярная ось, подобно щетке дворника стекло очистителя, начинает вращаться против (или по) часовой стрелки. Как только сумма заказов достигнет грузоподъемности транспортного средства, фиксируется сектор, обслуживаемый одним кольцевым маршрутом, и намечается путь объезда потребителей.

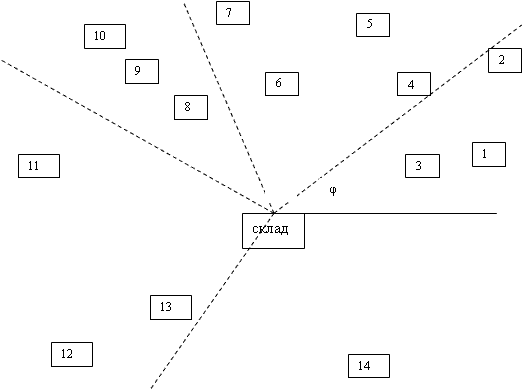
Рисунок 2.5.6 – Декомпозиция транспортной сети при составлении маршрутов

Составление кольцевого маршрута осуществляется путем решения задачи коммивояжера.

Решение задачи коммивояжера приведено на рисунке 2.5.7. Естественно, что в данном случае начальный и конечный пункты маршрута совпадают (распределительный склад).

Эта задача обладает всеми свойствами задач динамического программирования. Процесс решения разворачиваем от конца к началу. В конечный пункт (на склад) можно попасть из любого из магазинов, расстояния до которых приведены рядом с соответствующими стрелками (см. рис. 2.5.7).

В 4 магазин можно приехать из 5, 6 или 7; в 5 – из 4, 6 или 7; в 6 – из 4, 5 или 7; в 7 – из 4, 5 или 6.

В дальнейшем процесс решения разворачивается алогично. Слева от стрелок ставим суммарные расстояния.

Оптимальными оказываются маршруты «склад-7-6-5-4-склад» и «склад-4-5-6-7-склад», т. к. они обеспечивают минимальный километраж (15 км). Однако 4 магазин расположен ближе к складу, чем 7 магазин и целесообразнее ехать по маршруту «склад-4-5-6-7-склад», чтобы быстрее начать разгрузку (см. рис. 7.8).

Рисунок 2.5.8 – Оптимальный кольцевой маршрут

2. Исходные данные задачи оптимизации кольцевого маршрута

Исходными данными является таблица 2.5.27, однако, расстояния между магазинами, а также между магазинами и складом определяется схемой расположения этих объектов, которая формируется студентом самостоятельно.

2.5.9. Задача оптимизации прокладки дороги

Данная задача имеет очень большое экономическое значение. Ее решение особенно актуально в условиях освоения сибирского Севера, обладающего огромными запасами природных ресурсов, и может принести большой экономический эффект.

Задача решается методом динамического программирования.

1. Пример решения задачи оптимизации прокладки дороги

Планируется проложить дорогу из пункта А в пункт В. Имеется план местности, изображенной на рисунке 2.5.9.

Здесь приняты следующие обозначения (с указанием затрат на прокладку одного километра пути):

	– лес (50-100 у.д.е);
	– горы (150-200 у.д.е);
	– болото (100-150 у.д.е);
	– река (100-150 у.д.е без моста, 1-3 у.д.е – через мост);
	– поляна (5-15 у.д.е).

Рисунок 2.5.9 – План местности

По такому плану можно хотя бы примерно оценить стоимость прокладки дороги между любой парой рядом расположенных точек.

Для упрощения задачи, принимаем, что прокладка дороги может производиться только в направлениях Ю – С и З – В (юг – север и запад – восток). При более точных направлениях прокладки дороги (юг – сев.-зап., зап. – сев.-восток и пр.) суть задачи не меняется, только резко увеличивается ее размерность. Эта стоимость определяется рельефом местности, что отражено в примере на рисунке 2.5.10 над горизонтальными линиями и справа от вертикальных линий. На рисунке между кружками указана примерная стоимость прокладки дороги между соседними участками местности (без привязки к исходным данным, приведенным выше).

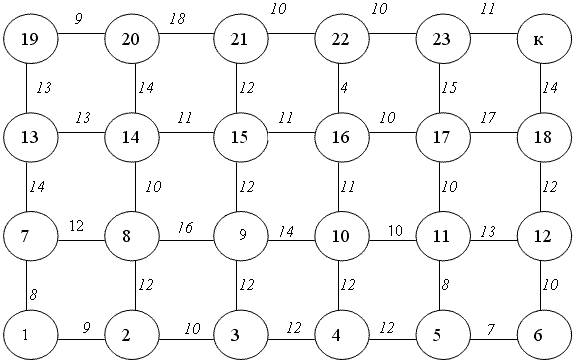
Рисунок 2.5.10 – Пример исходных данных оптимизации прокладки дороги

Здесь используются элементы теории графов. Кружки – вершины графа, соответствующие координатам участков местности. Соединяющие их линии – ребра графа – возможные участки дороги, соединяющие эти участки.

В конечное состояние система может перейти из состояния 23 с запада, или из состояния 18 с юга. Для этого требуются затраты материальных ресурсов в объеме 11 и 14, соответственно. Эти числа ставим над соответствующими кружками, и соответствующие пути обозначаем стрелками (см. рисунок 2.5.11).

Рисунок 2.5.11 – Пример решения задачи оптимизации прокладки дороги

В конечное состояние система может перейти с запада из состояния 22 через состояние 23 (для этого потребуется 11+10=21 стоимости), или с юга из состояния18 (для этого потребуется 12+14=26 стоимости). Ставим 21 и 26 над соответствующими кружками.

В конечное состояние система может перейти и из состояния 17. Причем, здесь появляются два альтернативных варианта: или через состояние 23 (на север), или через 18 (на запад). В первом случае суммарные затраты составят 26 (11+15=26), а во втором – 31 (14+17=31). Над кружком 17 ставим наименьшее из полученных чисел и стрелку направляем в состояние 23, обеспечивающее минимум затрат на прокладку пути на этом этапе.

Из состояния 16 в конечный пункт можно попасть через 22 и 23. Для этого потребуется 21+4=25. Однако из пункта 16 можно двигаться и через 17 и 23 (по стрелкам). В этом случае понадобится 26+10=36. Над кружком 16 ставим наименьшее из чисел и проводим соответствующую стрелку.

В дальнейшем процесс решения разворачивается алогично. Результатом решения является схема, изображенная на рисунке 7.11.

Из схемы следует, что минимально возможные суммарные затраты на прокладку пути – 77. Оптимальная траектория прокладки дороги, обеспечивающая минимум затрат: С-В-С-В-В-С-В-В.

2. Данные задачи оптимизации прокладки дороги

Данные задачи формируются студентом самостоятельно на основании придуманной им самим карты местности. Условные обозначения и соответствующие затраты на прокладку дороги следует взять в разделе 2.5.9.1. После этого студент без расчета намечает дорогу и определяет суммарные затраты на ее прокладку. Затем задача решается методом динамического программирования. Экономическая эффективность решения задачи определяется путем сравнения затрат на прокладку исходной и оптимальной дороги.

2.5.10. Определение оптимального срока
замены транспортного средства

Транспортные расходы, в том числе расходы на содержание транспортных средств, в структуре затрат на логистику занимают свыше 40%. Сократить эту статью расходов позволяет своевременная замена транспортного средства.

Дело в том, что при массовом характере сборки нет двух одинаковых автомобилей. Каждый из них «болеет» по-своему и каждый из них имеет свой век жизни даже при одинаковых условиях эксплуатации.

Проблема состоит в том, что чем больше «возраст» автомобиля, тем больше затраты на его содержание и поддержание в рабочем состоянии, и, в то же время, тем меньше цена его возможной реализации.

1. Пример решения задачи
замены транспортного средства

Автомобиль куплен за 40 тыс. у.д.е. (C₀=40) и эксплуатировался в течение шести лет, ежегодно проезжая в среднем по 20 тыс. км. Затраты на ремонт и рыночная стоимость автомобиля к концу каждого года приведены в таблице 2.5.28.

Таблица 2.5.28

Точка замены транспортного средства определяется минимальными общими затратами F(l), складывающимися из затрат на ремонт f_p(l), приходящихся на единицу выполненной работы l (пробег автомобиля), и величиной потребленного капитала f_k(l) на единицу работы.

Для построения графика f_p(l) необходимо определить:

1. затраты на ремонт Z_pi нарастающим итогом к концу каждого i-го года эксплуатации;
2. суммарный пробег автомобиля l_i к концу каждого l-го года эксплуатации.

(2.5.10)

Для построения графика f_k(l) необходимо определить:

1. величину необходимого капитала к концу каждого периода эксплуатации, как разницу между первоначальной стоимостью транспортного средства и его стоимостью на конец i-го периода

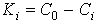(2.5.11)

2. величину необходимого капитала в расчете на 1 км пробега

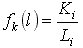(2.5.12)

Тогда суммарные капитальные затраты составят

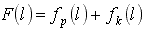(2.5.13)

Результаты расчетов следует занести в таблицу 2.5.29.

Таблица 2.5.29

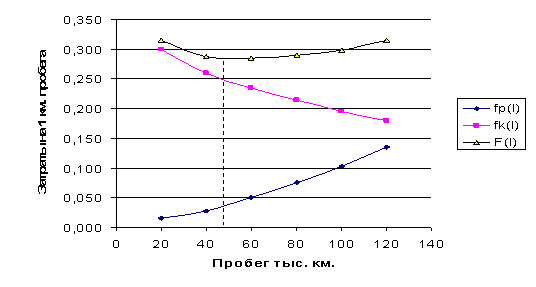
Рисунок 2.5.12 – Графическое определение оптимального
момента замены транспортного средства

2. Исходные данные задачи определения
момента замены транспортного средства

Автомобиль куплен за 40+F, где F – последняя цифра номера зачетки.

Остальные исходные данные приведены в таблице 2.5.30.

Таблица 2.5.30

Расчеты необходимо оформить алогично вышеприведенному примеру.

Расчет заключается определением экономической эффективности решения данной задачи путем сравнения найденных минимальных суммарных затрат с возможными затратами на конец седьмого года эксплуатации.