6. Математический аппарат,
применяемый при курсовом проектировании

6.6. Задачи сетевого планирования комплекса работ

Многие организационные и технические мероприятия представляют собой сложную совокупность взаимосвязанных работ. Примерами таких мероприятий могут быть строительство и реконструкция цехов и любых других объектов, освоение новой техники и технологии, производство проектно-конструкторских работ и пр. При реализации таких проектов возникает ряд проблем: определение рациональных сроков начала и окончания той или иной работы, обеспечивающих выполнение всего мероприятия за минимальное время; распределение ресурсов между работами, минимизирующее суммарные затраты. В частности, отдельные работы могут оказаться "узким местом", сдерживать проведение остальных мероприятий. Их следует выявить и выполнять заблаговременно или выделить на них дополнительные средства.

Сетевой график позволяет получить наглядное представление о порядке выполнения отдельных операций, а также о взаимосвязях между ними. Он является моделью реализации мероприятия, на которой можно изучать последствия тех или иных решений с целью выбора наилучшей стратегии управления.

На сетевом графике каждая работа изображается стрелкой, а факт ее окончания, называемый событием, обозначается кружком (рис. 6.14).

Рис. 6.14. Изображение работы и факта ее окончания на сетевом графике

Предположим теперь, что некоторая работа а₂ может начаться только после окончания работы а₁. В таком случае говорят, что работа а₂ опирается на работу а₁ (рис. 6.15).

Рис. 6.15. Работа а₂ опирается на работу а₁

Если же одна работа опирается на несколько других, то естественно, что она может начаться не ранее, чем закончится последняя из предшествующих. Логическая же связь со всеми остальными изображается в виде фиктивных работ, не требующих затрат времени и изображаемых пунктирными стрелками, идущими к началу данной работы. На рис. 6.16 работа а₄ опирается на а₁, а₂ и а₃, но позже всех заканчивается а₂.

Рис. 6.16. Фрагмент сетевого графика с фиктивными работами

Построение сетевого графика начинается с простого перечисления всех необходимых работ (графа 2 в табл. 6.4).

Таблица 6.4

Затем на основании простого логического анализа заполняется второй столбец таблицы и определяется ранг каждой работы. Работы первого ранга не опираются на другие. Работы второго ранга опираются только на работы первого ранга. Работы третьего ранга могут опираться на работы второго и первого рангов и т.д.

После этого производится перенумерация работ и заполняется последний столбец таблицы. При этом безразлично, в каком порядке присваивать номера работам одного и того же ранга.

После этого составляется новая таблица, в которой указывается продолжительность выполнения каждой работы (табл. 6.5).

Таблица 6.5

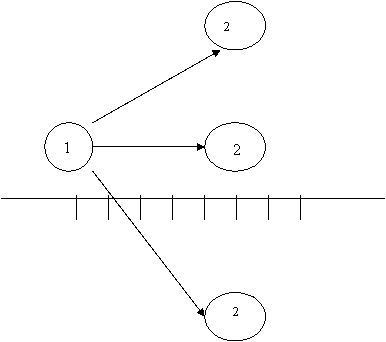
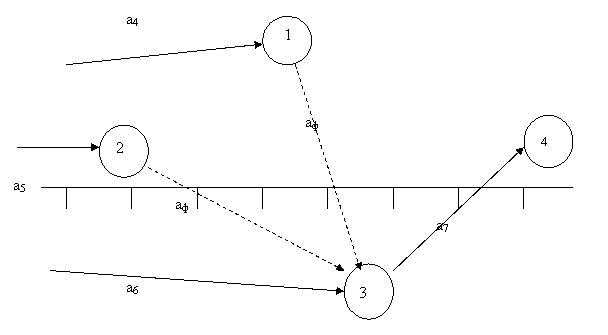
Существует несколько методов решения задач сетевого планирования. По-видимому, наиболее наглядным и простым является графоаналитический метод. При этом методе сначала проводится ось времени. В начале оси располагается исходный узел 0. Величина стрелки и угол ее наклона для любой работы выбираются рис., чтобы ее проекция на ось времени была равна ее продолжительности. Очевидно, что в этом случае есть множество вариантов изображения каждой работы. Например, на рис. 6.17 приведено три варианта изображения одной и той же работы.

Рис. 6.17. Варианты изображения одной и той же работы

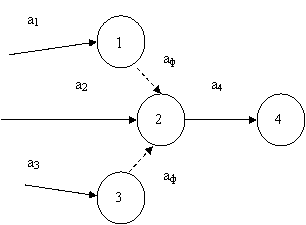
Если же одна работа опирается на несколько других, то изображающая ее стрелка должна начинаться из самого правого кружка, а логическая связь с другими работами изображается пунктирными стрелками (фиктивные работы). Пример этого случая приведен на рис. 6.18.

Рис. 6.18. Фрагмент временного сетевого графика с фиктивными работами

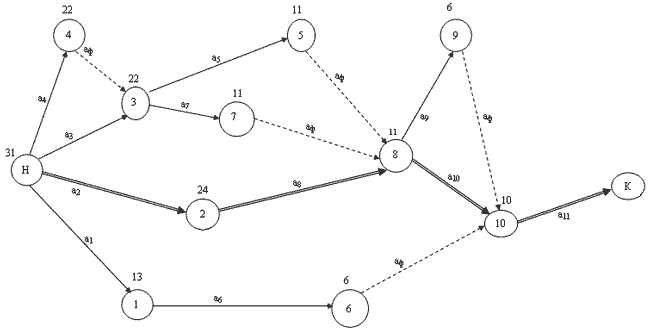
Сетевой график, построенный на основании исходных данных табл. 6.3, приведен на рис. 6.19.

Рис. 6.19. Сетевой график комплекса работ, построенный графоаналитическим методом

На графике двойными стрелками выделены критические работы. Критическая дуга составляется только из сплошных стрелок. Из графика, построенного графоаналитическим методом, сразу видна общая продолжительность производственного процесса. В данном случае Т_общ=31 день.

Фиктивные работы характеризуют резервы времени соответствующих реальных работ. Эти резервы определяются проекцией соответствующей фиктивной работы на ось времени. В данном случае работа а₄ имеет резерв времени в 2 дня, а₅ – 5 дней, а₇ – 9 дней, а₁ и а₆ – 18 дней и а₉ – 2 дня.

Знание этих резервов позволяет изменить сроки начала некритических работ и дать рекомендации о перераспределении имеющихся ресурсов в пользу критических работ с целью сокращения общей продолжительности выполнения всего комплекса.

Например, если а₆ – завоз оборудования, то его можно осуществить не сразу после завершения работы а₁, а на 12 дней позже. При этом не будет излишне загромождаться территория и само оборудование будет более сохранным.

Если же, например, работы а₂, а₇ и а₈ выполняются за счет трудовых ресурсов, с а₂ и а₇ вполне можно снять половину рабочих и перевести их на выполнение критических работ а₂ и а₈.

Задачам сетевого планирования присущи все свойства задач динамического программирования:

1. задача может быть разбита на этапы (по времени, в пространстве, этапы производственного процесса и пр.);
2. аддитивность решения – результат решения всей задачи может быть получен в результате суммирования результатов решения на каждом отдельном этапе;
3. регрессивность решения – решение разворачивается от конца к началу.

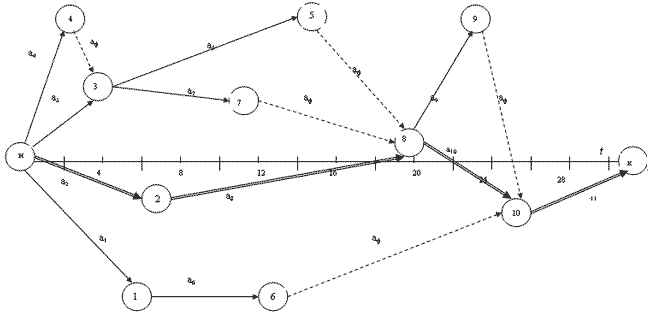
На рис. 6.20 показано решение той же задачи методом динамического программирования.

Рис. 6.20. Сетевой график комплекса работ, построенный графоаналитическим методом

Вначале безо всяких масштабов строится сетевой график. Для определения продолжительности выполнения всего комплекса работ, в соответствии с принципами динамического программиро-вания, процесс решения разворачивается от конца к началу.

В конечное состояние 11 система может перейти из состояния 10. Для этого потребуется 6 дней (а₁₁=6).

В состояние 10 система может перейти из состояния 6, 9 и 8. Максимальное время этого перехода составляет 5 дней (работа а₁₀). 9-10 и 6-10 – фиктивные работы, не требующие затрат времени, поэтому над кружками 9 и 10 ставим предыдущее число 6.

В состояние 8 система может перейти по дуге а₂-а₈, а3-а7, а4-а7, а3-а5 и а4-а5. Длины этих дуг (в днях) составляют соответственно 20, 11, 9, 15 и 13 дней. Наибольшей продолжительности требует переход системы из 2 в 8, а все остальные состояния соединяем с 8 фиктивными работами (пунктирными стрелками). Аналогичным образом доходим до начала производственного процесса.

Окончательный результат, естественно, получается точно таким же, как и при использовании графоаналитического метода.

Использование различных методов при решении одной и той же задачи позволяет исключить возможность появления даже случайной ошибки и широко используется в научных исследованиях и проектной практике.