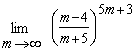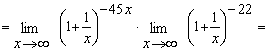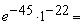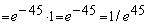Второй замечательный предел
Предел функции 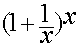 при
при 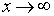 существует и равен числу
существует и равен числу 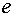 ;
;
число 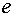 имеет значение
имеет значение 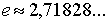 и является основанием системы натуральных логарифмов:
и является основанием системы натуральных логарифмов:
 .
.
Этот предел называют вторым замечательным пределом.
Если в нем положить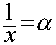 , то при
, то при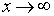 и
и
 и тогда
и тогда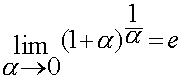 .
.
Пример 8. Найти предел 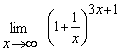 .
.
Решение:
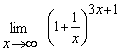 =
=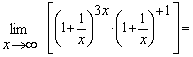
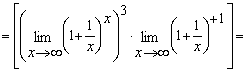
=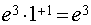 .
.
Пример 9. Найти предел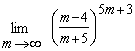 .
.
Решение: преобразуем основание
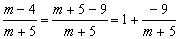 .
.
Тогда
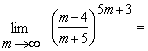
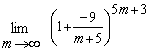 .
.
Чтобы представить полученный предел в виде второго замечательного предела, положим
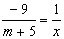 ,
,
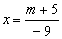 при
при
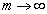 и
и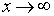 .
.
Выразим показатель степени через новую переменную.
Так как 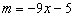 ,
,
то
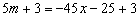 ,
,
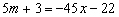 .
.
Тогда искомый предел примет вид
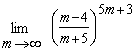

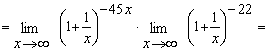
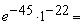
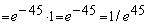
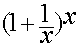 при
при 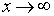 существует и равен числу
существует и равен числу 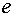 ;
;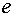 имеет значение
имеет значение 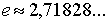 и является основанием системы натуральных логарифмов:
и является основанием системы натуральных логарифмов:  .
.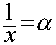 , то при
, то при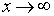 и
и
 и тогда
и тогда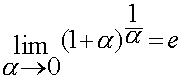 .
.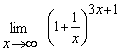 .
.
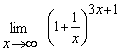 =
=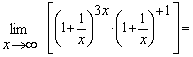
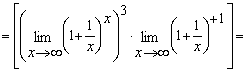
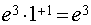 .
.
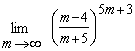 .
.
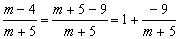 .
.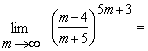
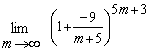 .
. 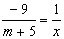 ,
,
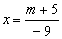 при
при
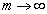 и
и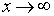 .
.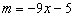 ,
,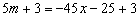 ,
,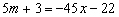 .
.