Инвестиционные решения. Исследование критериев
принятия решений с использованием функций Excel.
Основные понятия: простые и сложные проценты; текущая стоимость,
будущая стоимость, чистая дисконтированная стоимость.
При начислении процентов на вклад в банк
или другой финансовый институт (в том числе процент за кредит) принято
рассчитывать сложный процент. Формула
начисления сложных процентов: S = P*(1+ i)n , где
выражение (1+ i)n называют - Множитель наращения сложных
процентов (d ).
Условные обозначения:
Р – первоначальная
сумма вклада (кредита);
i – ставка простого процента;
I – проценты
за весь срок предоставления кредита;
T- срок
предоставления кредита;
S -
сумма, образовавшаяся к концу срока;
t – период начисления;
n = T/t - количество периодов начисления процентов.
При
начислении процентов поквартально, ставка годового процента делится на четыре
(количество кварталов в году).
Формула
простых процентов: S = P*(1+i*n).
При выработке долгосрочных решений и
компаниям, и частным предпринимателям необходимо знать, какую отдачу принесут
их инвестиции, и сопоставить прибыль от инвестирования средств в различные проекты. Расчет будущей стоимости (БС) инвестиции
проводят по формуле начисления сложных процентов:
Формула
расчета будущей стоимости инвестиции:
Будущая
стоимость (БС) = первоначальная сумма*(1+i)n
Для расчета текущей стоимости будущих поступлений
денежных средств также используется формула расчета сложного процента:
Формула
расчета текущей стоимости инвестиции:
Текущая
стоимость = Будущая стоимость / ( 1+i )n,
где
коэффициент 1/(1+i)n называется
коэффициентом дисконтирования, и в данном контексте процентная ставка i называется ставкой дисконта.
Применяя соответствующий коэффициент
дисконтирования, можно дисконтировать
будущие денежные потоки до их текущей стоимости. Разность между суммой
дисконтированных потоков и затратами определяет чистую дисконтированную
стоимость (ЧДС) инвестиции. Если полученное значение положительно, то
инвестирование средств является более выгодным, чем их помещение в банк под
процент. Если же ЧДС отрицательна, то инвестиция менее выгодна, чем помещение
средств в банк. Если же полученное значение равно
нулю, то норма прибыли на инвестицию равна ставке дисконта.
В Excel для вычисления будущего значения единой суммы вклада
или займа на основе постоянной процентной ставки методом сложных процентов
используется стандартная функция из раздела финансовых БС (или БЗ). Синтаксис
функции: БС (ставка; кпер; плт;
[пс]; [тип]), где:
ставка – процентная ставка за период;
КПер
– число периодов начисления (погашения);
Плт –
это выплата, производимая в каждый период. Это значение не может меняться в
течение всего периода времени;
ПС
– текущая, начальная стоимость
(первоначальная сумма) ;
ТИП – обозначает, когда должна производиться выплата: 0-в
конце периода, 1-в начале (если аргумент пропущен, по
умолчанию будет 0).
Для вычисления текущей
(приведенной) стоимости инвестиции используется функция из раздела финансовых ПС (или ПЗ). Синтаксис функции: ПС (ставка; Кпер; Плт; [бс];
[тип]). Для вычисления суммы дисконтированных потоков (суммируются текущие
стоимости будущих выплат) используется
функция из раздела финансовых ЧПС. Синтаксис функции:
ЧПС (ставка; значение1;
значение2;…).
Лабораторная
работа.1.
Задание:
Банк выплачивает по сберегательным
счетам 12% годовых, исчисляя сложные проценты каждый
квартал. Вы открыли счет на 5000 рублей. Сколько денег будет на вашем счету
через 2 года? Постройте гистограмму роста денег на счете в течение 2-х лет.
Решение:
В Excel для вычисления будущего значения единой суммы вклада
или займа на основе постоянной процентной ставки методом сложных процентов
используется стандартная функция из раздела финансовых БС (или БЗ). Синтаксис
функции: БС (ставка; кпер; плт;
[пс]; [тип]), где:
ставка – процентная ставка за период;
КПер
– число периодов начисления (погашения);
Плт –
это выплата, производимая в каждый период. Это значение не может меняться в
течение всего периода времени;
ПС
– текущая, начальная стоимость
(первоначальная сумма) ;
ТИП – обозначает, когда должна производиться выплата: 0-в
конце периода, 1-в начале (если аргумент пропущен, по
умолчанию будет 0).
1.
Вводим исходные
данные на лист Excel, предварительно разбив
период начисления на кварталы – за два года их будет восемь. Ставка процента за
период начисления i равна 3%
(12/4), т.к. по условию задачи сложные проценты начисляются поквартально.
Процентная ставка по вкладу или кредиту записывается в ячейке со знаком
процента, либо в виде сотых долей. Первоначальную сумму вносим в ячейку со
знаком минус «-», т.е. эту сумму
вы должны банку (рис.19).

Рисунок 19.
2.
В ячейку Е2 вводим формулу для вычисления будущего значения вклада,
используя функцию БС: = БС (ставка; кпер; плт; [пс]; [тип]). Формула в
ячейке Е2 будет иметь вид: = БС(В2;
D2; ; А2; 0).
Полученный результат 6333,85 – сумма вашего вклада через 2 года (рис.19).
3.
Для построения
диаграммы роста вклада поквартально, необходимо рассчитать будущее значение
суммы вклада для каждого квартала (8 кварталов – столбец D). В ячейку Е2 вводим формулу
для вычисления будущего значения вклада, где аргумент КПер
будет равен 1 (1 квартал). Формула в ячейке Е2 будет
иметь вид: БС($В$2; D2; ;$А$2; 0), которую скопируйте вниз по столбцу до
ячейки Е9 включительно. Полученные данные использовать для построения
гистограммы (рис. 20).
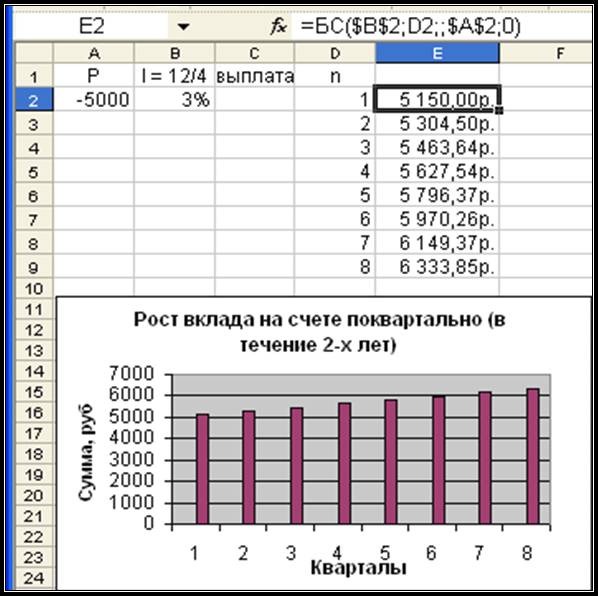
Рисунок 20.
Лабораторная работа 2.
Задание:
Определить сумму, которую сегодня следует
положить в банк, чтобы через пять лет на
счету было 100 000 рублей, и при этом ежегодно снимать с вклада 3000 рублей. Процентная ставка банка
15% годовых.
Решение:
1.
Вводим исходные данные на лист Excel.
Первоначальную сумму указываем произвольно, например, 6000 рублей (ячейка А2)
на рисунке 21.
2.
Для вычисления будущего значения вклада используем стандартную функцию БС: = БС
(ставка; кпер; плт; [пс]; [тип]).
3.
В ячейке Е2 получен отрицательный результат. Явно, что
6000 рублей недостаточно для накопления 100000 рублей при выполнении всех
условий.
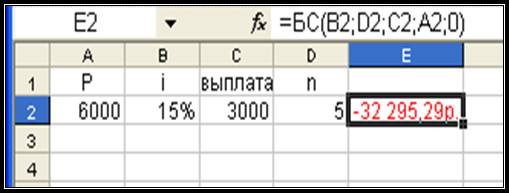
Рисунок 21.
4.
Выделить ячейку Е2 и выбрать команду Сервис-Подбор параметра. В
диалоговом окне в поле Значение ввести 100000, а в поле Изменяя значение ячейки – А2.
5.
В ячейке А2 проставлена сумма, которую вы должны положить в банк - 59774 рублей (рис.22):

Рисунок 22.
6.
Измените условия задачи: Определите сумму вклада, чтобы через 3 года вы смогли
получить в банке 50000 рублей, ежегодно снимая 6000 рублей, процентная ставка
банка 12% годовых.
Лабораторная работа 3.
Задание:
Компания
«Синтез» располагает старыми станками, от которых необходимо избавиться. От
других организаций (фирм) поступили следующие предложения:
1.
Фирма
«Металлолом» по переработке
предлагает:
Сумма
31000 рублей выплачивается единовременно через три года
2.
Компания по
реализации «Альфа»:
Сумма
10000 выплачивается немедленно, затем в течение трех лет 6000 тыс. рублей выплачиваются в конце каждого года
3.
Частный
предприниматель (ЧП) Иванов А.И.
Сумма
25000 выплачивается единовременно через
2 года.
Какое предложение выгоднее, если текущая ставка
дисконта составляет 5% годовых и сложный процент
начисляется ежегодно?
Решение:
Для решения задачи необходимо сопоставить текущую
стоимость трех предложенных методов оплаты путем дисконтирования сумм,
которые будут получены в будущем.
В Excel для вычисления текущей (приведенной) стоимости
инвестиции используется функция из раздела финансовых ПС
(или ПЗ). Синтаксис функции: ПС (ставка; Кпер; Плт; [бс]; [тип]).
1.
Вводим исходные данные на лист Excel (заполнение ячеек столбцов A, B, C) – рисунок 23.
2.
В ячейках D3, D7, D15 c использованием функции ПС получены результаты расчетов
текущей стоимости. Результаты показаны со знаком «-», т.к. все операции
проходят через банк и минус обозначает , что эти
деньги (первоначальные суммы) сдают в банк.
3.Формула
в ячейке D7 составлена для первого года
выплаты, копируем её вниз для второго и третьего годов (при этом адреса ячеек А7 и С7 будут абсолютными). Суммируем текущие стоимости за
три года, а также 10000 рублей, которые выплачиваются немедленно и, в целом в
рамках данного предложения (компания «Альфа») текущая стоимость составляет
26339, 49 рублей.
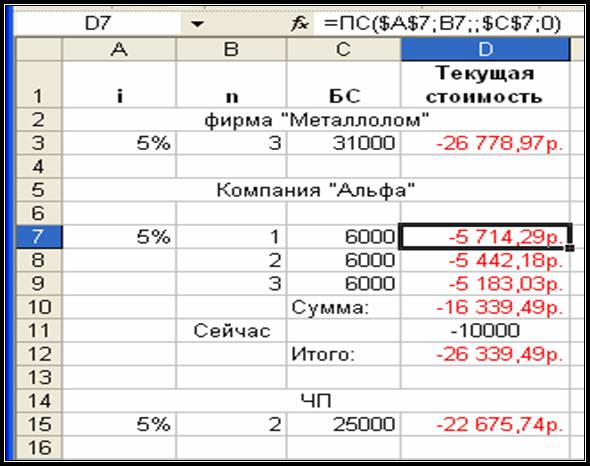
Рис. 23. Таблица вычислений текущей (дисконтированной)
стоимости.
4.
Сравнивая полученные результаты (ячейки D3, D12
и D15) очевидно, что предложение фирмы «Металлолом» предполагает самую высокую
текущую стоимость (26778,97 рублей) и по этой причине является наиболее
выгодным (рис.23).
Лабораторная работa 4.
Расчет
дисконтированного потока денежных средств.
Задание:
Первоначальная
инвестиция в размере 450000 рублей, как ожидается, обеспечит положительные
потоки денежных средств в размере 115000, 135000,
145000 и 160000 рублей в конце последующих четырех лет соответственно.
Определить, является ли данная инвестиция рентабельной при ставке дисконта 8% и
12%.
Решение:
В Excel для вычисления суммы
дисконтированных потоков (суммируются текущие стоимости будущих
выплат) используется функция из раздела
финансовых ЧПС. Синтаксис функции:
ЧПС (ставка; значение1;
значение2;…).
1.
Исходные данные, представленные в таблице 18
ввести на лист Excel.
Таблица 18.
|
Период |
Денежные
средства |
|
Сейчас
(затраты) |
-450000 |
|
Будущие
выплаты: |
|
|
Конец
первого года (значение
1) |
115000 |
|
Конец
второго года (значение
2) |
135000 |
|
Коней
третьего года (значение
3) |
145000 |
|
Конец
четвертого года (значение 4) |
160000 |
2. В ячейках D5 и D10 (рис. 25) c
использованием функции ЧПС (рис.24.)
рассчитать суммы дисконтированных потоков будущих выплат.
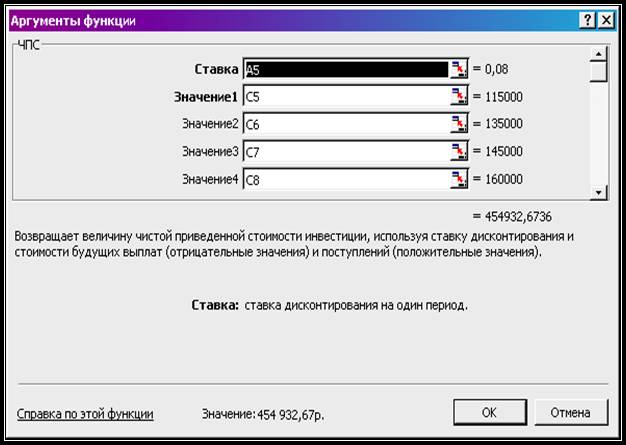
Рис.24. Диалоговое окно функции ЧПС.
3.
Чистая дисконтированная стоимость определяется как разность между суммой
дисконтированных потоков и затратами (450000 рублей):
ЧДС
= ∑ ДС - затраты
Расчет ЧДС выполнить в ячейках F5 и F10 и результаты должны соответствовать данным этих
ячеек на рисунке 25.
Таким
образом, при банковской ставке 8% ЧДС
положительная и инвестиционный проект будет рентабельным. При ставке дисконтирования 12%
ЧДС отрицательная и данный проект нерентабельный.
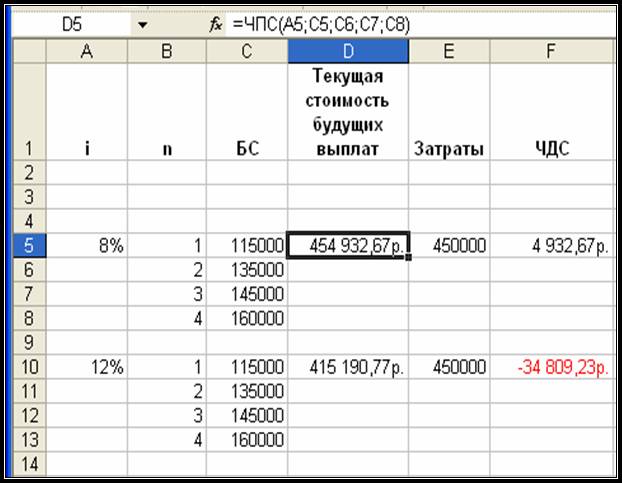
Рис. 25.
Результаты вычислений дисконтированных потоков и ЧДС.