Технологии прогнозирования деятельности предприятия с помощью Microsoft Excel.

 

Основные понятия.

Технологии  прогнозирования основываются на   двух важнейших методах составления прогноза:

·       Анализ временных рядов;

·       Корреляция и регрессионный анализ

В основе АНАЛИЗА ВРЕМЕННЫХ РЯДОВ – допущение о наличии информации за ряд прошлых периодов. Эти данные позволяют выявить долгосрочные тенденции и повторяющиеся циклы.

При отсутствии данных за прошлые периоды прибегают к КОРРЕЛЯЦИИ:  рассматривают   показатели  с целью выявления возможной взаимосвязи между ними. И далее применяют технику проведения РЕГРЕССИОННОГО АНАЛИЗА для построения уравнения, описывающего  выявленную взаимосвязь.

 

 Прогнозирование на основе зависимости между двумя переменными (корреляция и регрессия).

 

В регрессионном анализе изучается односторонняя зависимость переменной Y  от одной или нескольких переменных Х1 …., Хk. Основная задача регрессионного анализа – установление формы зависимости между зависимой (Y) и независимыми (Х1 …., Хk) переменными и анализ достоверности параметров этой зависимости. Такие переменные, как расходы на рекламу, транспорт, численность населения и т.п. являются независимыми переменными, а те переменные, которые мы пытаемся оценить (например, объем продаж), являются зависимыми переменными.

Схема составления прогноза заключается в сборе данных о значениях зависимых и независимых переменных, их анализе на предмет наличия связи (корреляция) и выведении математического уравнения, описывающего эту связь (регрессия).

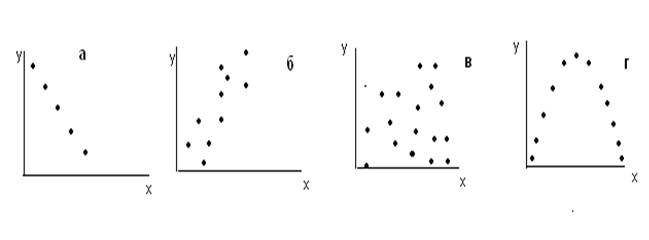
Первая стадия корреляционного анализа – сбор данных о значениях переменных и составления точечных диаграмм (ХY-диаграммы). Точечные диаграммы имеют различный вид:

Так, на рис. а пример абсолютной отрицательной корреляции, на рис.б  – сильной положительной корреляции. На рис. в – взаимосвязь между значениями не усматривается, на рис. г взаимосвязь наличествует, но это не линейная зависимость, а параболическая.

Предположение наличия линейной зависимости между двумя переменными основывается на значении коэффициента корреляции r, который рассчитывается по формуле:

,                                (1.1)

 

где n – число пар значений переменных, а Σ символ суммирования.

 

Значение коэффициента корреляции колеблется от -1 ( в случае абсолютной отрицательной корреляции) до +1 (в случае абсолютной положительной корреляции). Такие диаграммы как  показаны на рис. в, г, дадут коэффициенты корреляции почти равные нулю. Хотя на рис. г   точки взаимосвязаны между собой, но там зависимость параболическая, а коэффициент корреляции измеряет тесноту линейной связи. Это свидетельствует о важности не только расчетов, но и рассмотрения точечной диаграммы, поскольку даже при r близким к нулю возможно тесная взаимосвязь, но не линейная, а, например, параболическая как показано на рис. г.

Если установлена тесная линейная корреляция между переменными, то можно вывести уравнение прямой и использовать её для прогнозирования поведения зависимой переменной в будущем. Этот процесс носит название ЛИНЕЙНОЙ РЕГРЕССИИ.

Уравнение прямой (линейной) регрессии имеет общий вид:

Y = a + b*x,

где y – результативный показатель; х – независимая переменная (фактор); a и b представляют собой константы, их значения определяют положение и направленность прямой в осях координат.

 Константа а называется точкой пересечения прямой с осью ординат и её значение представляет собой значение у, когда х=0. Константу b называют коэффициентом при х.

Задача регрессионного анализа заключается в экспериментальном определении коэффициентов регрессии, путем наблюдения за характером изменения входных параметров (факторов) и выходной величины (результативного показателя). Линейная модель уравнения регрессии строится по методу наименьших квадратов. Этот критерий минимизирует сумму квадратов вертикальных отклонений точек от прямой регрессии.

В реальных процессах зависимость результативного показателя у зависит от целого ряда переменных (факторов) х1, х2, …,хk. – и это будет множественная регрессия. Модель множественной регрессии имеет следующий вид:

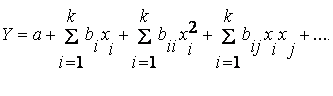                        (1.2)    

j ≠ i,

 где bi – линейные коэффициенты,  bii – нелинейные коэффициенты, bij- коэффициенты, учитывающие взаимное влияние факторов.

 

Для анализа общего качества регрессии используют коэффициент детерминации (определенности) R2. Он характеризует долю вариации (разброса) зависимой переменной, объясненной с помощью данного уравнения. Т.е. с увеличением объясняемой доли разброса R2 à1.

Значимость уравнения регрессии определяют, используя критерий Фишера (F-критерий). Расчетное значение Fв  сравнивается с  критическим значением (Fкр), определяемого по таблице критических точек распределения Фишера: Fкр = k/n–k – 1;  где k - число факторов, (n-k-1) – число степеней свободы знаменателя  и n – это число параллельных опытов. Если Fв > Fкр  - то полученное уравнение регрессии значимо, т.е. хотя бы один из коэффициентов уравнения не равен нулю.

Значимость коэффициентов регрессии проверяется с помощью t-критерия, основанного на распределении Стьюдента.  Если вычисленный t-критерий коэффициента bi ( çtbi ê) больше tкр., то коэффициент значимый и влияние соответствующего фактора значимо. tкр  определяют по уровню значимости и числу степеней свободы f = n-k-1.

 В табличном процессоре MS Excel значения статистических функций удобно вычислять при помощи мастера функций. Для выполнения статистического анализа имеется набор средств анализа данных, называемый Пакет анализа. Для работы с дополнением Пакет анализа  следует задать Сервис-Анализ данных. При отсутствии в меню этой команды следует задать Сервис - Надстройки и в появившемся диалоговом окне Надстройки включить переключатель Пакет анализа, нажать кнопку ОК. Начнет загружаться пакет Анализ данных.

В пакете Анализ данных инструмент Регрессия предлагает линейный регрессионный анализ, который заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Для вычисления коэффициентов регрессии, определяющих нелинейную зависимость и взаимное влияние факторов необходимо факторы переобозначить.  Например, выходной параметр Y зависит от трех факторов: y = f(x1, x2, x3).

Записываем значения этих факторов, квадраты факторов, их взаимные произведения и переобозначаем их: x1® x1, x2® x2, x3®x3,  ® x4,  x®x, x®x,  x®x,  x®x,  x®x,  x®x. В результате можно построить линейную модель с использованием уравнения (1.2) вида:

y = b0+ b1x1 + b2x2 + b3x3 + b4x4 + b5x5 + b6x6 + b7x7 + b8x8 + b9x9 + b10x10.

Проведя обратные переобозначения, получим модель, учитывающую нелинейность и взаимное влияние факторов:

y = b0+ b1x1 + b2x2 + b3x3 + b11x + b22 x + b33x + b12x1x2 + b13x1x3 + b23x2x3 + b123x1x2x3.

 

 

 

Лабораторная работа 1.1.

Составление прогноза с использованием линейного  уравнения   регрессии. Расчет коэффициента корреляции.

Задание:

Отдел маркетинга компании по продаже модной одежды «Пандора» намеревается изучить наличие взаимосвязи между объемом продаж в каждом отделении сети магазинов фасонной одежды  и численностью населения, проживающего в радиусе 30-минутной езды от каждого из отделений.

Отдел располагает  данными  среднего еженедельного оборота в десяти отделениях сети магазинов компании и сведениями о численности населения:

 

Отделение

магазина

 

Объём продаж, тыс. руб.

 

Численность населения

 

1

24

287

2

15

161

3

18

75

4

22

191

5

43

450

6

35

323

7

32

256

8

25

312

9

19

142

10

23

210

 

1. В Excel на основе исходных данных сформировать таблицу, которая будет состоять из 3 столбцов и 11 строк и занимать блок ячеек А1:С11 (табл. 1).

2. Постройте точечную диаграмму, используя данные ячеек В2:С11. По диаграмме охарактеризовать зависимость между переменными – объемом продаж (Y) и численностью населения (Х).

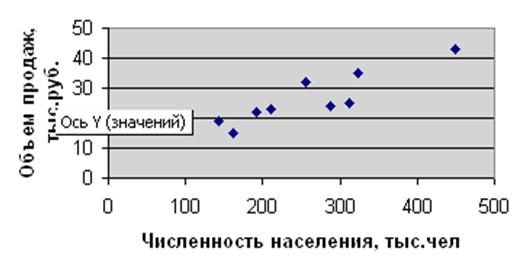
Рис. 1.  Точечная диаграмма. - Взаимосвязь между объемом продаж и численностью населения.

 

Точки на диаграмме образуют область, похожую по форме на прямую линию, что указывает на существование тесной положительной корреляции между рассматриваемыми переменными.

2. Для подтверждения корреляционной связи и наличия линейной зависимости  между двумя переменными – объёмом продаж и численностью населения необходимо провести  расчет коэффициента корреляции – r (коэффициент корреляции измеряет тесноту линейной связи).

Вычисления выполнить, используя пакет  Анализ данных инструмент Корреляция (входной интервал - В2 : С11; группирование - по столбцам), или используя функцию  КОРРЕЛ (категория: Статистические).

Если рассчитанное значение r близко к +1, это подтверждает наличие сильной корреляционной (линейной) связи между объемом продаж и численностью населения.

 3. На основе линейной регрессионной модели исследовать зависимость объема продаж (у) от численности населения (х), используя пакет Анализ данных,  инструмент Регрессия:

Входной интервал Y: С2:С11  - столбец данных объема продаж; 

Входной интервал Х: В2:В11;

Константа – ноль – флажок не устанавливать, чтобы линия регрессии не проходила через начало координат;

установить флажки – Остатки и Нормальная вероятность

Результаты вычислений представляют собой таблицу, блоки ячеек такой таблицы, необходимые для дальнейших вычислений показаны на рис.2.

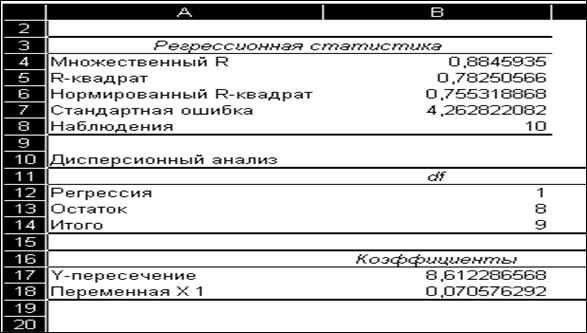
Рис.2. Блоки ячеек из отчета с результатами анализа «Регрессия».

 

4. Используя результаты анализа «Регрессия» (рис.2.)  записать уравнение регрессии У = а + b*х , которое будет  имеет вид:

у = 8,61 +  0,07х,

5. Занести  значения коэффициентов регрессии а и b в таблицу 1.

 

Таблица 1.

 

A

B

C

D

1

Магазин

 

Численность населения

Х

Объём продаж

 

Y

Прогноз

2

1

287

24

= $C$14 + $C$15*В2

3

2

161

15

 

4

3

75

18

 

5

4

191

22

 

6

5

450

43

 

7

6

323

35

 

8

7

256

32

 

9

8

312

25

 

10

9

142

19

 

11

10

210

23

 

12

 

750

 

 

13

 

 

 

 

14

Константа (Y-пересечение)  (а)

8,6122866

 

15

Коэффициент при Х (b)

0,0705763

 

 

6. Для расчета прогноза в таблице 1 справа добавить колонку «Прогноз» и в ячейку D2 ввести формулу регрессии для  прогноза объема продаж при уровне населения 287 тыс.чел.  Формула, которую нужно ввести в D2: = $C$14 + $C$15*В2. В формуле используются значки $  для ссылок на ячейки со значениями коэффициентов а и b, постоянными для всех вычислений в данной задаче. Скопировать формулу по всем ячейкам столбца «Прогноз».

7. Спрогнозируем объём продаж магазина фасонной одежды, если население, проживающее в пределах 30-минутной езды от него, составляет 750 тыс.чел. (т.е. х = 750).  Расчеты выполнить в  таблице 1, добавив  строку для данных в 750 тыс.чел.

8. Сделать выводы по прогнозу, используя термины – интерполяция (прогноз для х, находящегося в пределах интервала значений х) и экстраполяция. Сравнить фактические данные с вашим прогнозом.

9. Интерпретация основных показателей из отчета результатов регрессионного анализа:

         В отчете результатов регрессионного анализа на рис.2. верхняя строка называется «Множественный R» - это значение коэффициента корреляции r (= 0,885). На следующей строке приведено значение R-квадрат. Коэффициент определенности (R2 ) показывает, какая часть зависимой переменной (переменной Y) объясняется уравнением регрессии. В нашем примере значение R2 (R-квадрат)  составляет 0,782506, или 0,783. Таким образом, можно утверждать, что в соответствии с уравнением регрессии 78,3% вариаций объема торговли объясняются изменением численности населения.

 

 

 Лабораторная работа 1.2.

Cоставление прогноза с использованием уравнения множественной регрессии.

Задание: На основе линейной регрессии исследовать зависимость объема продаж (у) от  размера торговой площади (х1)  и численности персонала (х2) по результатам наблюдений, заданных в следующей таблице:

Таблица 2.

 

 

A

B

C

D

1

№ предприятия

Объем продаж, тыс.руб.

Размер торговой площади, кв.м.

Численность персонала, чел.

2

1

90

10

10

3

2

272

15

14

4

3

130

20

11

5

4

228

20

12

6

5

192

27

11

7

6

280

33

11

8

7

240

37

11

9

8

296

49

10

10

9

280

52

11

11

10

320

32

14

 

 

1. Для проведения регрессионного анализа использовать инструмент Регрессия, пакета Анализ данных:

Входной интервал Y: диапазон анализируемых зависимых данных (В2:В11), диапазон должен состоять из одного столбца;

Входной интервал Х: диапазон независимых данных (С2:D11);

Константа – ноль – нет (при установленном флажке линия регрессии проходит через начало координат);

Уровень надежности – установить флажок, использовать уровень 95%;

Отметить флажком параметры вывода Остатки и График нормальной вероятности (рис. 3):

 

 

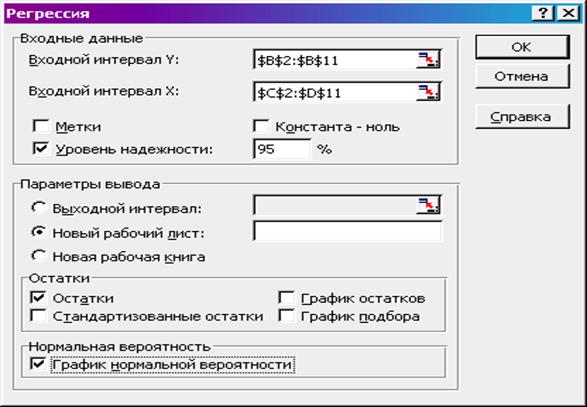
Рис. 3. Окно инструмента Регрессия

 

1.               Excel представит решение в виде 5 таблиц. На рисунке 4   показаны и выделены основные характеристики из таблиц с результатами. Вычисленное значение F= 20, 35 и это больше чем Fкр = 4,74. Значение 4,74 – это табличное значение (Приложение 1) Excel представит решение в виде 5 таблиц. На рисунке 4   показаны и выделены основные характеристики из таблиц с результатами. Вычисленное значение F= 20, 35 и это больше чем Fкр = 4,74. Значение 4,74 – это табличное значение (Приложение 1) при вероятности 0,05; где число степеней свободы числителя равно 2, число степеней свободы знаменателя равно 7. Таким образом, полученное уравнение регрессии значимо.

 Проверяем значимость коэффициентов при Х1  (4,42) и при  Х2  (35,4):  с помощью таблицы критических точек распределения Стьюдента (Приложение 2)  при вероятности = 0,05 и f = 10-2-1 = 7 определяем tкр  = 2,365.

 çtх1 ê больше tкр  : 5,49 > 2,365, коэффициент при Х1 значим;

  çtх2 ê больше tкр : 4.53 > 2,365, коэффициент при Х2 значим.

2.               2, число степеней свободы знаменателя равно 7. Таким образом, полученное уравнение регрессии значимо.

 Проверяем значимость коэффициентов при Х1  (4,42) и при  Х2  (35,4):  с помощью таблицы критических точек распределения Стьюдента (Приложение 2)  при вероятности = 0,05 и f = 10-2-1 = 7 определяем tкр  = 2,365.

 çtх1 ê больше tкр  : 5,49 > 2,365, коэффициент при Х1 значим;

  çtх2 ê больше tкр : 4.53 > 2,365, коэффициент при Х2 значим.

Регрессионная статистика

 

 

 

Множественный R

0,92373

 

 

 

R-квадрат

0,85327

 

 

 

Нормированный R-квадрат

0,81135

 

 

 

Стандартная ошибка

32,4672

 

 

 

Наблюдения

10

 

 

 

 

 

 

 

 

Дисперсионный анализ

 

 

 

 

Df

SS

MS

F

Регрессия

2

42910,77954

21455,38977

20,35389386

Остаток

7

7378,820457

1054,117208

 

Итого

9

50289,6

 

 

 

 

 

 

 

 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Y-пересечение

-304,787

99,01892383

-3,078064836

0,017863878

Переменная X 1

4,41941

0,805016513

5,489842412

0,00091635

Переменная X 2

35,4099

7,803802551

4,537519931

0,002675596

Рис.4. Результаты регрессионного анализа

 

3.  Используя результаты анализа «Регрессия» (рис.4)  записать уравнение регрессии У = а + b1*х1 + b2*x2 , которое будет  имеет вид:

у = - 304,8 +  4,419х1 + 35,41x2 ;

5. Занести  значения коэффициентов регрессии в исходную таблицу (ячейки F2, F3, F4) и  спрогнозировать объем продаж, используя уравнение регрессии  у = - 304,8 +  4,419х1 + 35,41x2 ;

6. В ячейку Е2 вводим формулу уравнения: у=$F$2+$F$3*C2+$F$4*D2 и копируем её вниз по столбцу.

 Результаты прогноза представлены в столбце E таблицы 3.

 

Таблица 3.

 

A

B

C

D

E

F

1

№ пред-приятия

Объем продаж

размер торговой площади

численность персонала

Теор. объем продаж (прогноз)

Коэфф.

2

1

90

10

10

93,50657

-304,787

3

2

272

15

14

257,2433

4,419414

4

3

130

20

11

173,1106

35,40991

5

4

228

20

12

208,5205

 

6

5

192

27

11

204,0465

 

7

6

280

33

11

230,563

 

8

7

240

37

11

248,2406

 

9

8

296

49

10

265,8637

 

10

9

280

52

11

314,5319

 

11

10

320

32

14

332,3733

 

 

 

 

 

Прогнозирование на основе анализа временных рядов.

Временной ряд -        это ряд наблюдений, проводившихся регулярно через равные интервалы времени. Он может быть равен году, неделе, суткам или даже минутам, в зависимости от характера рассматриваемой переменной.

 

 

 Прогнозирование с применением метода скользящего среднего.

         Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее – начиная с третьего и т.д.  Таким образом, при расчетах среднего уровня как бы «Скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.

         Интервал сглаживания, т.е. число входящих в него уровней определяют, используя следующее правило: если необходимо сгладить мелкие, беспорядочные колебания, то интервал сглаживания берут по возможности большим; если же нужно сохранить более мелкие волны и освободиться от периодически повторяющихся колебаний – интервал сглаживания уменьшают.

 

Лабораторная работа 1.3.

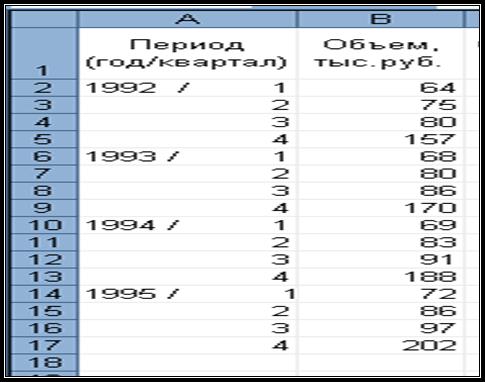
Для прогнозирования объема продаж необходимы средние значения данного показателя за последние несколько лет. В таблице 4   представлены ежеквартальные объемы продаж компании, специализирующегося на розничной продаже детских игрушек.

 

 

 

                                                                                         Таблица 4.

                                         

I.     Один из способов создания скользящего среднего в Excel является прямое введение формулы. Так, чтобы получить 4-х квартальное скользящее среднее, нужно ввести формулу:                  = СРЗНАЧ (B2:B5)  в ячейку C4 и скопировать эту формулу, соответственно, вниз до ячейки C16 включительно. Если записать формулу в ячейку C6, то это приведет к потере некоторых  показателей скользящего среднего (рис. 5). В данном случае у временного ряда имеется сезонная вариация, при этом показатель скользящего среднего имеет тенденцию к увеличению.

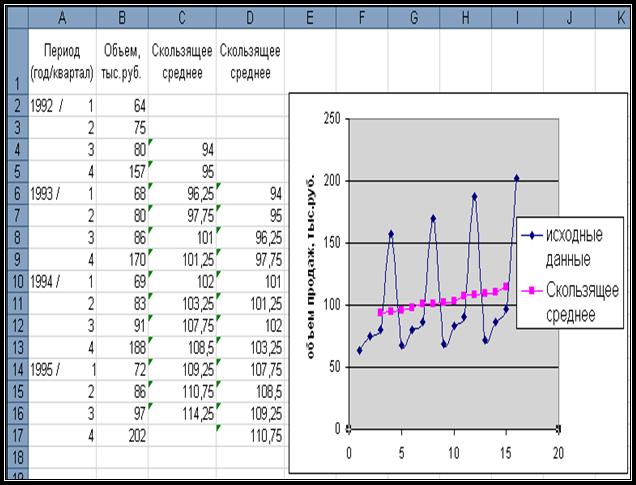
Рис. 5.  Исходные данные и скользящее среднее объема продаж.

 

II.       Другим способом создания скользящего среднего является использование надстройки Пакет Анализа, инструмента анализа Скользящее среднее:

1.В меню Сервис выбрать команду Анализ данных. Появится диалоговое окно Анализ данных, где из списка выбрать инструмент Скользящее среднее (рис.6 ).

Рис. 6. Окно инструмента Скользящее среднее.

 

3.    В поле Входной интервал указать диапазон В2:В17

4.    В поле Интервал ввести количество кварталов, которое включается в подсчет скользящего среднего - 4. Интервал сглаживания  (по умолчанию используется значение 3) определяют, используя правило: если необходимо сгладить мелкие колебания временного ряда, то интервал берут по возможности большим, если нужно сохранить мелкие волны – интервал сглаживания уменьшают.

5.    В поле Выходной интервал ввести адрес ячейки (или щелкнуть на этой ячейке в рабочем листе) для вывода результатов.

6.    Поставить значки для вывода графика и стандартных погрешностей.

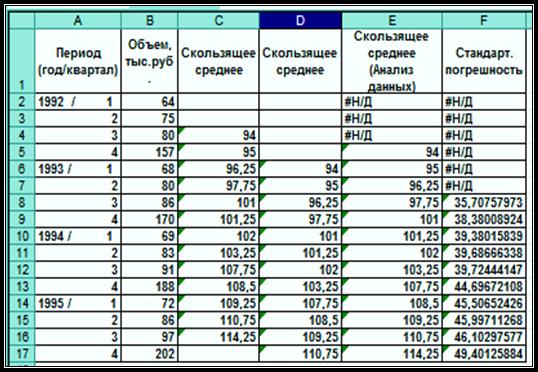
7.    Excel представит результаты решения  в столбцах E и F (табл. 5) с выводом  графика (рис. 7). Если предшествующих данных недостаточно для построения прогноза, Excel возвратит ошибочное значение #Н/Д.

 

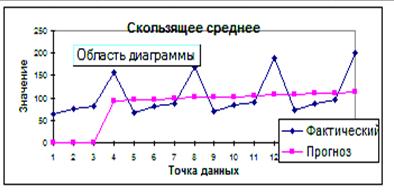
Рис. 7. График Скользящее среднее.

 

 

 

 

 

 

 

 

 

 

 

 

Таблица 5.

 

 

 

Прогнозирование с использованием метода Экспоненциального сглаживания.

 

При прогнозировании с применением метода сглаживания учитывается отклонение предыдущего прогноза от реального показателя, а сам расчет проводится по следующей формуле:

f k = f k-1  + a (x k-1– f k-1),                                    (   1.1.   )

 где:   f k-1   - прогноз в момент времени k-1;

           f k      - прогноз на момент времени tk, следующий за периодом k-1;

          x k-1  - реальное значение показателя в момент времени t k-1;

         a  - постоянная сглаживания (0< a >1)определяет степень сглаживания.

Если при сравнении прогноза с реальными значениями сглаженные данные при выбранном  a  значительно отличаются от исходного ряда, необходимо перейти к другому параметру сглаживания (чем больше значение  a, тем больше сглаживание)

 

 

 

Лабораторная работа 1.4.

1. В ячейки А2:В17 (рис. 9) ввести исходные данные объема продаж из таблицы 4. Для составления прогноза используем инструмент Экспоненциальное сглаживание  пакета Анализ данных:

2. Выполнить следующие команды – Сервис – Анализ данных – Экспоненциальное сглаживание – ОК.  В появившемся окне инструмента Экспоненциальное сглаживание (рис. 8) указать следующие значения:

 

Рис. 8.  Окно инструмента Экспоненциальное сглаживание

 

Входной интервал – В2:В17;

Фактор затухания (константа сглаживания a) – 0,3 (значение по умолчанию – 0,3);

Выходной интервал: С12;

Поставить флажки для вывода графика и стандартных погрешностей.

Excel представит результаты решения в следующем виде  - рис.  9.

Диапазон С2:С13 – рассчитанные значения экспоненциального сглаживания по формуле  ( 1.1. );

Диапазон D2:D17 – рассчитанные значения стандартных погрешностей.

Если предшествующих данных недостаточно для построения прогноза, Excel возвращает ошибочное значение #Н/Д.

 

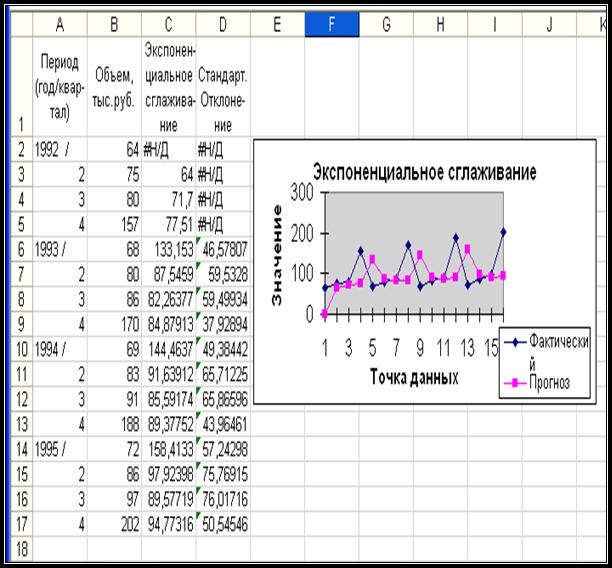
Рис. 9.  Результаты решения задачи с помощью инструмента Экспоненциальное сглаживание.

 

 

 

 Прогнозирование на основе тренда.

 

Тренд – это общая долгосрочная тенденция изменения временного ряда, лежащая в основе его динамики. Первая стадия анализа временных рядов – построение графика данных. Программа Excel позволяет построить тренд непосредственно на графике данных и на его основе сделать прогноз о развитии изучаемого процесса на предстоящий промежуток времени.

В Excel существует шесть различных типов линий  трендов (аппроксимация и сглаживание), которые могут быть добавлены в диаграмму Excel:

· линейная;

· логарифмическая;

·  полиномиальная (степень полинома можно устанавливать от 2 до 6);

·  степенная;

·  экспоненциальная;

· линейная фильтрация.

Возможно также построение линий трендов на основе скользящих средних.

Линии тренда позволяют графически отображать тенденции данных и прогнозировать данные.

Построение линий трендов выполняется в следующей последовательности:

1.               На основе введенных данных на лист Excel с помощью мастера диаграмм построить диаграмму. Нагляднее всего выбрать тип диаграммы График, вид – график с маркерами, помечающими точки данных.

2.               Щелкнув правой кнопкой мыши непосредственно на диаграмме, выбрать из появившегося контекстного меню команду Добавить линию тренда. На экране появится диалоговое окно Линия тренда. На вкладке Тип из шести предложенных выбрать один из типов линии тренда. При выборе типа Полиномиальная в поле Степень необходимо указать степень полинома (возможен выбор от 2 до 6). При выборе типа Линейная фильтрация в поле Точки следует указать количество наблюдений, которое включается в любое вычисление скользящего среднего (возможен выбор от 2 до 10).

3.               Раскрыть вкладку Параметры. На вкладке Параметры:

·       В секции Название аппроксимирующей (сглаженной) кривой установить один из переключателей —

автоматическое и тогда название будет указано справа от этого указателя,

другое, тогда в поле справа следует ввести с клавиатуры желаемое название тренда.

·       В секции Прогноз указать длительность прогноза (число периодов прогноза вперед или назад).

·       Установленный флажок пересечение кривой с осью y в точке 0 приведет к тому, что линия тренда будет проходить через начало координат.

·       Флажок показывать уравнение на диаграмме содействует появлению на графике уравнения тренда в виде текста. Excel может расположить уравнение таким образом, что оно перекроет некоторые данные графика или линии тренда. В этом случае следует выделить это уравнение, щелкнув на нем мышью, а затем перетащить его в другое, более удобное место.

·       Флажок поместить на диаграмму величину достоверности аппроксимации (R2) показывает на диаграмме величину надежности построенного тренда. Значение коэффициента детерминации R2 – это оценка точности адекватной модели. При подборе линии тренда к данным Excel автоматически рассчитывает R2 и по требованию отображает это значение на диаграмме. Выводимое значение R- квадрат (коэффициент детерминации) определяет, с какой степенью точности полученное уравнение аппроксимирует исходные данные. Если R2  ³ 0,95 , то говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если 0,8 £ R2 < 0,95 , то говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если 0,6 £ R2 < 0,8 , то говорят о слабой аппроксимации (модель слабо описывает изучаемое явление). Если R2  < 0,6 , то говорят, что точность аппроксимации недостаточна и модель требует изменения.

4.               Чтобы удалить линию тренда, следует выделить её и нажать [Del].

 

 

Лабораторная работа 1.5.

1. В ячейки А2:В17 (рис. 9) ввести исходные данные объема продаж из таблицы 4. Для составления прогноза используем инструмент Экспоненциальное сглаживание  пакета Анализ данных:

2. Выполнить следующие команды – Сервис – Анализ данных – Экспоненциальное сглаживание – ОК.  В появившемся окне инструмента Экспоненциальное сглаживание (рис. 8) указать следующие значения:

 

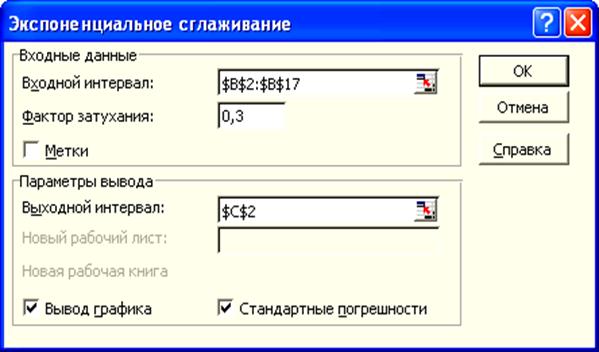
Рис. 8.  Окно инструмента Экспоненциальное сглаживание

 

Входной интервал – В2:В17;

Фактор затухания (константа сглаживания a) – 0,3 (значение по умолчанию – 0,3);

Выходной интервал: С12;

Поставить флажки для вывода графика и стандартных погрешностей.

Excel представит результаты решения в следующем виде  - рис.  9.

Диапазон С2:С13 – рассчитанные значения экспоненциального сглаживания по формуле  ( 1.1. );

Диапазон D2:D17 – рассчитанные значения стандартных погрешностей.

Если предшествующих данных недостаточно для построения прогноза, Excel возвращает ошибочное значение #Н/Д.

 

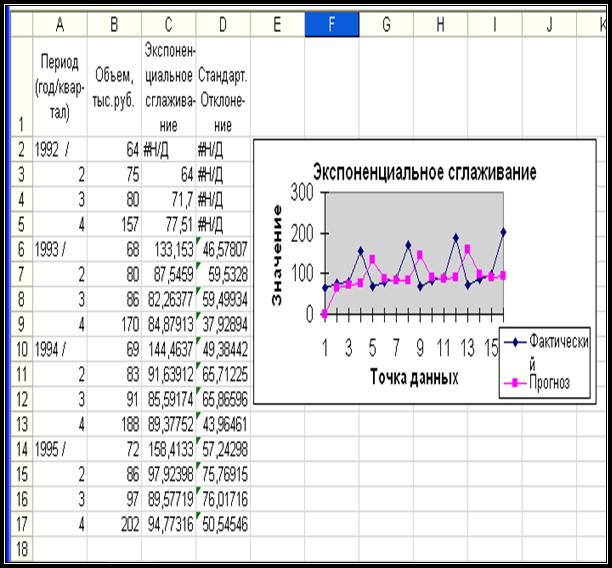
Рис. 9.  Результаты решения задачи с помощью инструмента Экспоненциальное сглаживание.

 

 

Лабораторная работа 1.5.

Задание:

При организации нового Видеокафе было решено, что с каждого человека плата не должна превышать 5$. Требуется определить входную плату, при которой выручка будет наибольшей и составить прогноз работы видеокафе при увеличении входной платы до 12 $.

         Опыт работы подобных Видеокафе показал следующую динамику значений  посещаемости кафе в зависимости от входной платы:

 

Входная плата (х),

Количество посетителей (у)

1,50

17,500

2,00

16,000

2,50

14,000

3,00

12,5000

3,50

11,000

4,00

  9,200

5,00

  7,000

 

1.    Ввести исходные данные на лист Excel.

2.    С помощью мастера диаграмм построить график посещений видеокафе в зависимости от входной платы.

3.    Построить линии трендов с использованием линейной, логарифмической, полиномиальной и экспоненциальной функций. Для каждой из этих функций показать на графике уравнение кривой и величину достоверности аппроксимации R2 (R2  показывает степень приближения тренда к фактическим значениям динамического ряда).

Графическое представление данных (с использованием логарифмической,  полиномиальной функций) и уравнения кривых должны  выглядеть так:

 

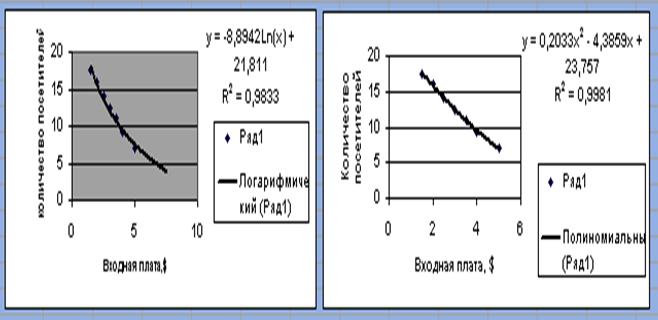
Рис. 10. Логарифмический и полиномиальный типы  линий тренда.

 

4.    По величине R2 определить кривую, которая наиболее точно воспроизводит характер изменения исследуемых показателей (с максимальным значением R2). Эту кривую оставить на графике, остальные удалить.

5.    Итак, выбранное уравнение кривой (полиномиальный тип):          

у = 0,2033х2 - 4,3859х + 23,757  (у = ах2 – bх + c)

Полученные коэффициенты а, b (коэффициенты при х), заносим в таблицу данных (табл. 6).

6.  По уравнению рассчитать Количество посетителей теоретическое - в ячейку F2 ввести формулу: = $D$2*A2^2 - $E$2*A2 + 23,757 Скопировать формулу по всем ячейкам столбца.

В таблицу добавить столбцы: Выручка экспериментальная и Выручка теоретическая. Для расчетов использовать формулу:

 

Выручка = (количество посетителей) * (входная плата) 

 

Результаты  вычислений представлены в таблице 6.

7. Используя метод наименьших квадратов минимизируем Погрешность-отклонение теоретических данных от фактических. Отклонение по выручке рассчитать по формуле = (G2 – C2)^2, которую записываем в ячейку Н2 и копируем соответственно вниз по столбцу, до ячейки Н8 включительно. Теперь необходимо посчитать Погрешность, используя формулу: = СУММ (Н2 : Н8). Формулу записываем в ячейку Н9.

     Таблица  с вычислениями должна выглядеть так (табл.6):

Таблица 6.

 

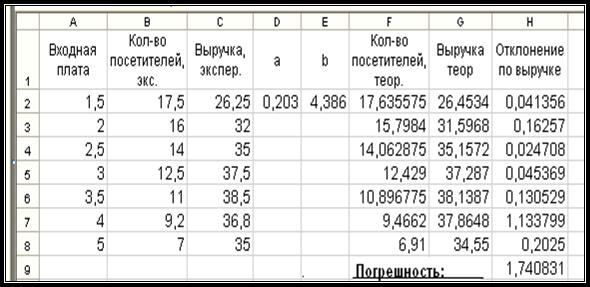
8.    С помощью сервисной функции Поиск решения (Сервис- Поиск решения) подобрать коэффициенты при х – а и b, стараясь минимизировать погрешность.  Отвечаем на вопросы диалогового меню:

 

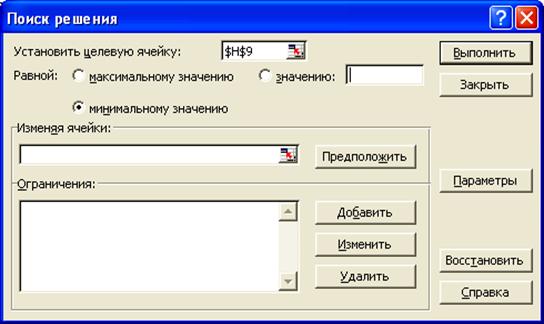
Рис. 11.   Использование функции Поиск решения.

 

(При неправильном заполнении нажать кнопку Восстановить)

Ответив на вопросы диалогового меню (рис. 11), нажать кнопку Выполнить. Программа выдает  запрос на сохранение найденного решения (сохранить)  и выбрать тип отчета – Результаты.

        

 В итоге результаты вычислений будут выглядеть так (рис.12):

 

Рис.12. Результаты вычислений с помощью функции Поиск решения.

 

9. По уравнению кривой с обновленными коэффициентами а = 0,21103;   b = 4,4186 (табл. 7)  определяем входную плату, при которой выручка будет максимальной. Для этого, анализируя исходные (экспериментальные данные) отмечаем, что максимальная выручка получена при стоимости билета 3,5$  - при соблюдении условия задачи, когда входная плата не должна превышать 5$. Таким образом, прогнозируем максимальную выручку при входной плате в интервале от 3,5$ до 4$ - в столбце А таблицы 7 заполним ячейки значениями входной платы, соответственно 3,6:  3,7 …. до 4,0$.  Затем копируем формулы ячеек F8 и G8, соответственно  вниз, и смотрим прогноз Количества посетителей и Выручки для интервала входной платы от 3,5 до 4$. Данные таблицы указывают, что максимальная выручка может быть получена при входной плате 3,63$  или 108,9 рублей (по курсу 1$=30 руб.)                                                                                          

 

 

 

Таблица 7.

 

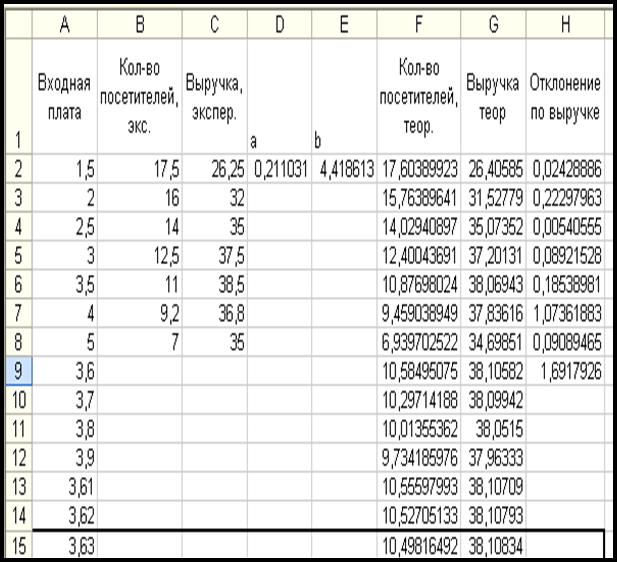
10. Изменяя в столбце А (начиная с ячейки А16 и вниз)  значение входной платы, продолжить процесс прогнозирования количества посетителей  и выручки при повышении цены билета  до 12$.

 

 

Лабораторная работа 1.6.

Задание: Составить прогноз роста народонаселения России, используя сведения из статистического справочника за период с 1960 по 1995гг. (таблица 8).

Таблица 8. Исходные данные

Год

Численность населения, млн.чел.

1960

117,5

1970

130,1

1980

137,6

1990

147,4

1991

148,5

1992

147,7

1993

148,7

1994

148,4

1995

148,3

 

         Для решения поставленной задачи необходимо знать вид функциональной зависимости, связывающей количество жителей и время, а также коэффициенты этой зависимости. Для определения коэффициентов используются экспериментальные данные, для нахождения же вида зависимости нужны либо теоретические предпосылки, либо подбор экспериментальных видов зависимости.

         Известно, что теоретическая зависимость имеет экспоненциальный вид: f(x)=aebx. Для нахождения этой функциональной зависимости осуществляем подбор значений коэффициентов а и b. Сначала определим их значения приближенно, для чего построим график роста статистической численности и аппроксимируем его. Это осуществляется с помощью представления на графике линии тренда. Для построения линии тренда необходимо:

1.    выделить линию графика;

2.    выполнить команду меню Диаграмма – Добавить линию тренда;

3.    выбрать экспоненциальный тип;

4.    выбрать в диалоге Линия тренда вкладку параметров и установить флажок Показывать уравнение на диаграмме и флажок Поместить на диаграмму величину достоверности аппроксимации (R2).

В результате на графике появится линия тренда и уравнение с подобранными коэффициентами а и b.

 

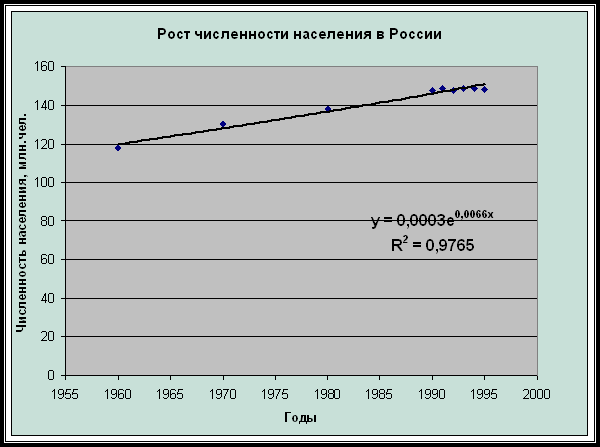Рис. 13.  Линия тренда, уравнение и значение R2

 

5.          По уравнению у=0,0003е0,0066х  рассчитываем теоретические значения функции (е – основание натурального логарифма, равное 2,718…).

6.          Далее по таблице 9 (согласно методу наименьших квадратов) вычисляем величину отклонения S, то есть сумму квадратов разности теоретических и фактических значений функции. В ячейку D2 записываем  формулу:  = (B2-C2)^2 и копируем соответственно вниз по столбцу, до ячейки D10 включительно. Теперь необходимо посчитать Отклонение S (погрешность), используя формулу: = СУММ (D2 : D10).

7. Минимизируем погрешность (S = 381, 298513) с использованием сервисной функции Excel Поиск  решения (подробный ход действий дан в лабораторной работе № 1.5). Полученные коэффициенты (a, b) из Отчета  по результатам  работы надстройки Поиск  решения изменили теоретические значения  функции – таблица 10.

 

 

 

Таблица 9.

 

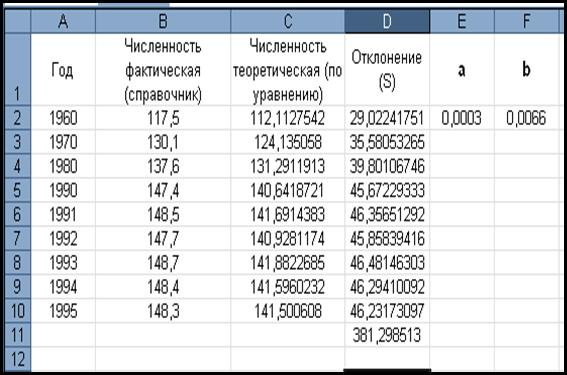
Таблица 10.

 

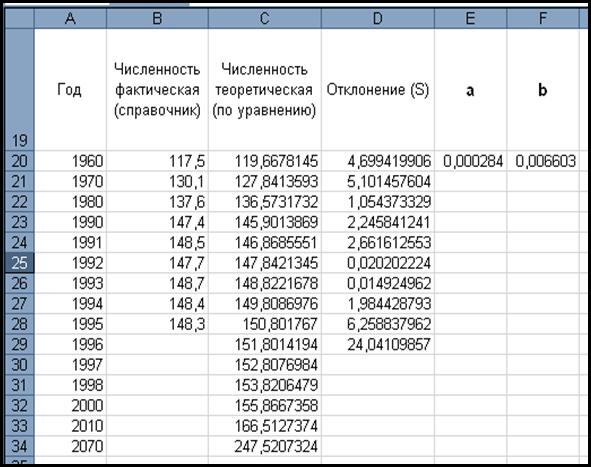
8. Далее по новому уравнению функции  прогнозируем  численность населения в России до 2070 года, копируя формулу уравнения вниз по столбцу С.

 

 

 Прогнозирование с помощью функций Excel - ТЕНДЕНЦИЯ и РОСТ.

 

         Прогнозирование с использованием статистической функции ТЕНДЕНЦИЯ основано на линейной связи между результатом наблюдения и временем, в которое это наблюдение было зафиксировано. То есть функцию ТЕНДЕНЦИЯ можно рассматривать как наиболее простой  способ линейного регрессионного анализа.

Если взаимосвязь (по диаграмме) явно нелинейная, то для прогноза используется функция РОСТ. Существует большое количество типов данных, которые изменяются во времени нелинейным способом. Примерами таких данных являются – объем продаж  новой продукции; прирост населения и др.

 

Лабораторная работа 1.7.

Задание: Используя исходные данные лабораторной работы № 1.6 (табл. 8, 10), составить прогноз численности населения с помощью статистических функций ТЕНДЕНЦИЯ  и РОСТ.

I. Исходные данные внести в ячейки А2:В10 (таблица 11). В ячейку С2 ввести формулу: =ТЕНДЕНЦИЯ (В2:В10;А2:А10;;ИСТИНА) и получаем результат = 119,3603.

         Далее для ввода формулы массива выделяем ячейки С2:С10,  нажимаем клавишу F2 и далее комбинацию клавиш <Ctrl +Shift + Enter>. Полученные данные (С2:С10) прогнозируют базовую линию результатов фактических наблюдений.

         Для составления прогноза на новые временные моменты (А11:А14) в ячейку С11 вводим с помощью формулы массива следующее:

{= ТЕНДЕНЦИЯ(В2:В10; А2:А10;А11:А14;ИСТИНА)}

Excel вернет в ячейки С11-С14 прогноз на временные моменты  с 1997г. по 2000г

II. При составлении прогноза с использованием функции РОСТ все действия аналогичные заданию I (c использованием функции ТЕНДЕНЦИЯ ). Но функция ТЕНДЕНЦИЯ возвращает значения в соответствии с линейной аппроксимацией по методу наименьших квадратов, а функция РОСТ возвращает значения в соответствии с экспоненциальным трендом. В таблице 11 представлены результаты прогнозов с использованием 3-х методов: на основе тренда и функций ТЕНДЕНЦИЯ и РОСТ.

                                                                                                           

                                                                                                Таблица 11.