ТЕМА 1.2. Кинематика
1.2.1. Траектория, путь, перемещение. Скорость
1.2.2. Вычисление пройденного пути
Тест 1.2.2.
1.2.3. Ускорение
1.2.4. Нормальное и тангенциальное ускорение
Тест 1.2.4.
1.2.5. Кинематика вращательного движения. Угловые скорости и ускорение
Тест 1.2.5.
1.2.1. Траектория, путь, перемещение. Скорость
МТ при движении описывает некоторую линию, называемую траекторией. В зависимости от формы траектории различают прямолинейное движение, движение по окружности, криволинейное движение и др. Пусть МТ переместилась вдоль некоторой траектории из точки 1 в точку 2 (Рис. 1.2.1).
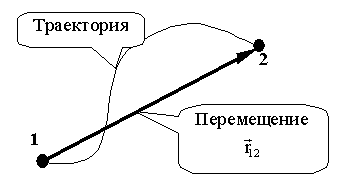
Рис. 1.2.1. Траектория и перемещение материальной точки
Расстояние между этими точками, измеренное при движении МТ по траектории, имеет значение пройденного пути s. Направленный отрезок прямой, проведенный из точки 1 в точку 2, называется перемещением. Перемещение - это величина, характеризующаяся численным значением и направлением, имеет геометрический смысл вектора. Действительно, пусть имеем одинаковые по величине перемещения МТ из точки 1 в точку 2 и 3 (Рис. 1.2.2, а).
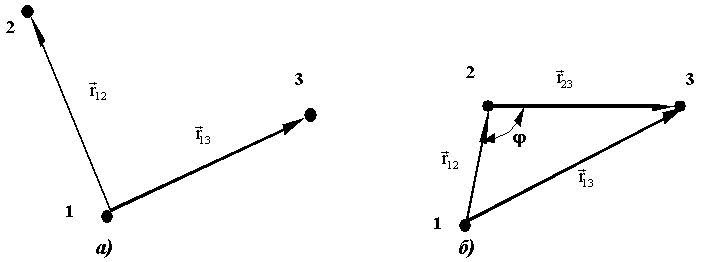
Рис. 1.2.2. Векторы перемещения материальной точки:
а) неэквивалентность результата перемещения при одинаковой длине вектора;
б) сложение векторов
Очевидно, что, хотя величины перемещений одинаковы, результат далеко не равноценен, поскольку МТ оказывается в разных пространственных положениях. Если МТ совершает сложное движение, которое можно описать, например, двумя последовательными перемещениями
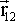 и и
 , то суммарное перемещение можно задать одним вектором , то суммарное перемещение можно задать одним вектором
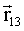 (Рис. 1.2.2, б), который задает такое же перемещение. Результат сложения векторов определяется соотношением: (Рис. 1.2.2, б), который задает такое же перемещение. Результат сложения векторов определяется соотношением:
Квадрат модуля вектора (1.2.1) в общем случае можно вычислить, используя теорему косинусов:
где φ - угол между векторами
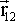 и и
 . .
К числу векторных величин в механике относят скорость, ускорение, силу и ряд других. Длина отрезка в установленном масштабе имеет смысл модуля вектора, стрелкой показывают направление вектора.
Величины, для определения которых достаточно знать одно число, называются скалярными (скалярами). Скалярами являются путь, время, масса, температура и другие.
Положение МТ в пространстве будем задавать с помощью радиус-вектора
 ,
проведенного из начала координат системы отсчета в МТ. При движении МТ вектор ,
проведенного из начала координат системы отсчета в МТ. При движении МТ вектор
 может изменяться как по величине, так и по направлению. Рассмотрим вектор
может изменяться как по величине, так и по направлению. Рассмотрим вектор
 в некоторый момент времени t (Рис. 1.2.3). в некоторый момент времени t (Рис. 1.2.3).
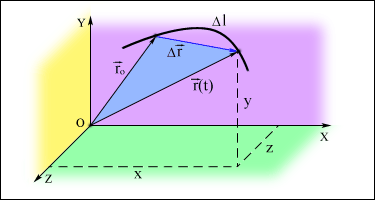
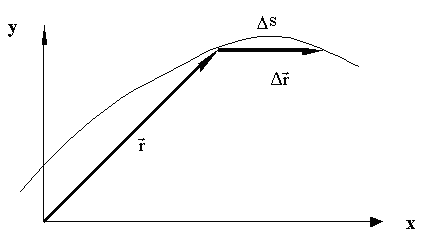
Рис. 1.2.3. Радиус-вектор материальной точки в зависимости от времени
За малый (элементарный) промежуток времени Δt МТ проходит элементарный путь Δs, который можно представить с помощью вектора элементарного перемещения
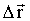 . Возьмем отношение: . Возьмем отношение:
которое также является вектором, совпадающим по направлению с вектором
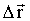 .
Ясно, что это отношение зависит от величины промежутка времени Δt. Будем уменьшать знаменатель дроби (1.2.3). При этом будет уменьшаться и числитель. Однако такое уменьшение происходит до определенного предела так, что при достижении весьма малых значений Δt вектор .
Ясно, что это отношение зависит от величины промежутка времени Δt. Будем уменьшать знаменатель дроби (1.2.3). При этом будет уменьшаться и числитель. Однако такое уменьшение происходит до определенного предела так, что при достижении весьма малых значений Δt вектор
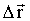 прекращает изменяться как по величине, так и по направлению. Следовательно, отношение (1.2.3) стремится к некоторому пределу, который называют скоростью МТ в момент времени t: прекращает изменяться как по величине, так и по направлению. Следовательно, отношение (1.2.3) стремится к некоторому пределу, который называют скоростью МТ в момент времени t:
По определению, соотношение (1.2.4) представляет собой производную по времени:
и называется истинной или мгновенной скоростью МТ. Из Рис. 1.2.4 ясно, что вектор
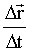 является секущей траектории движущейся МТ. является секущей траектории движущейся МТ.

Рис. 1.2.4. Скорость как секущая траектории материальной точки
В пределе (1.2.4) секущая (скорость МТ) превращается в касательную к траектории. Этот вывод можно распространить на любую траекторию.
Элементарный путь Δs в общем случае отличается от модуля элементарного перемещения
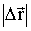 .
Однако, если временной промежуток Δt → 0, то различие между Δs и .
Однако, если временной промежуток Δt → 0, то различие между Δs и
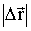 также становится исчезающе малым. Благодаря этому для модуля скорости можно записать:
также становится исчезающе малым. Благодаря этому для модуля скорости можно записать:
1.2.2. Вычисление пройденного пути
Из соотношения (1.2.6) следует, что при малых Δt приближенно выполняется:
Равенство (1.2.7) выполняется тем точнее, чем меньше промежуток Δt. Если известно, как скорость зависит от времени, можно вычислить путь, пройденный МТ с момента времени
t1 до момента t2. Для этого разобьем промежуток времени t2 - t1 на N малых промежутков: Δt1,
Δt2,..., ΔtN. Весь путь s также представим как сумму путей, проходимых за соответственные промежутки Δti:
Δs1, Δs2,..., ΔsN, так что выполняется:
Используя (1.2.7), можно приближенно представить:
где vi - значение скорости на промежутке Δti.
Подставляя (1.2.9) в (1.2.8), получим:
В пределе при стремлении к нулю всех промежутков Δti сумма, стоящая в правой части (1.2.10), будет точно равна пути:
Скорость есть функция времени v = v(t). В математическом анализе в общем виде для произвольной функции f(x) задают определенный интеграл следующим образом:
Тогда путь, пройденный МТ за промежуток времени от t1 до t2, равен определенному интегралу:
Согласно определению геометрического смысла интеграла, путь, пройденный МТ за промежуток времени от t1 до t2, численно равен площади фигуры, ограниченной графиком функции v(t), осью времени t и прямыми t1 и t2 (Рис. 1.2.5).
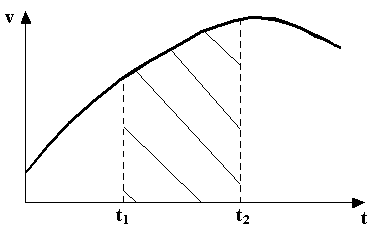
Рис. 1.2.5. Геометрическая интерпретация пути
Движение, при котором скорость, изменяясь как угодно по направлению, не меняется по величине, называют равномерным. Тогда все значения vi в формуле (1.2.11) будут одинаковыми, и общий множитель можно вынести за знак суммы, при этом сумма временных промежутков равна времени t. В результате приходим к простому соотношению:
Из (1.2.14) следует, что при равномерном движении скорость равна пути, деленному на время:
1.2.3. Ускорение
Быстрота изменения скорости МТ со временем - ускорение - характеризуется величиной:
Из (1.2.16) следует, что, если известны ускорение как функция времени
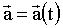 и начальная скорость и начальная скорость
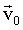 , то можно найти скорость МТ в любой момент времени: , то можно найти скорость МТ в любой момент времени:
Если ускорение постоянно (движение МТ равноускореннное), то из (1.2.17) следует:
При прямолинейном движении вектор скорости все время направлен вдоль одной и той же прямой - траектории, вследствие чего направление вектора ускорения совпадает с вектором скорости или противоположно ему. Если вектор ускорения параллелен вектору скорости, то скорость растет и движение будет ускоренным. Если вектор ускорения антипараллелен вектору скорости, то скорость уменьшается и движение будет замедленным. Прямолинейное движение с постоянным ускорением называют равнопеременным. Взяв соотношение для скорости в проекции на ось х так, что эта ось совпадает с начальной скоростью, имеем:
Проекции vx, v0x, ax равны модулям соответствующих векторов, взятых со знаком "плюс", если направление вектора совпадает с осью х, взятых со знаком "минус", если направление вектора противоположно оси х. Интегрируя функцию (1.2.19) в пределах от нуля до произвольного момента времени t, получим формулу для пути при равнопеременном движении:
1.2.4. Нормальное и тангенциальное ускорение
Рассмотрим равномерное движение МТ по окружности. Пусть в рассматриваемый момент времени t МТ находится в положении 1 (Рис. 1.2.6).

Рис. 1.2.6. Равномерное движение по окружности радиуса R
Спустя промежуток Δt МТ окажется в положении 2, пройдя путь Δs, равный дуге 1-2. При этом скорость МТ 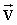 получает приращение получает приращение
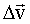 , в результате чего вектор скорости, оставаясь неизменным по величине (при равномерном движении по окружности , в результате чего вектор скорости, оставаясь неизменным по величине (при равномерном движении по окружности
 ), повернется на угол Δφ, совпадающий по величине с центральным углом, опирающимся на дугу длиной Δs: ), повернется на угол Δφ, совпадающий по величине с центральным углом, опирающимся на дугу длиной Δs:
где R - радиус окружности, по которой движется МТ.
Найдем приращение вектора скорости 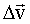 . Для этого перенесем вектор . Для этого перенесем вектор  параллельно самому себе так, чтобы его начало совпадало с началом вектора параллельно самому себе так, чтобы его начало совпадало с началом вектора
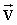 . Тогда вектор . Тогда вектор
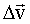 будет изображен отрезком, проведенным из конца вектора будет изображен отрезком, проведенным из конца вектора 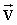 в конец вектора в конец вектора
 . Этот отрезок служит основанием равнобедренного треугольника со сторонами . Этот отрезок служит основанием равнобедренного треугольника со сторонами
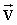 и и
 и углом Δφ при вершине. Для малых Δt угол Δφ невелик, поэтому приближенно можно записать: и углом Δφ при вершине. Для малых Δt угол Δφ невелик, поэтому приближенно можно записать:
Если ввести единичный вектор  , тогда можно записать: , тогда можно записать:
Подставляя (1.2.21) в (1.2.23), имеем:
Разделив обе части (1.2.24) на Δt и переходя к пределу, получим ускорение:
В этом выражении v и R - постоянные величины;
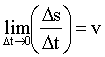 ;
единичный вектор ;
единичный вектор 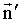 в пределе совпадет с единичным вектором в пределе совпадет с единичным вектором 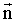 , нормальным к окружности в точке 1 и направленным к центру. Следовательно, можно записать: , нормальным к окружности в точке 1 и направленным к центру. Следовательно, можно записать:
Найденное таким образом ускорение направлено по нормали к траектории; его называют нормальным ускорением и обозначают символом 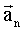 . Модуль нормального ускорения равен: . Модуль нормального ускорения равен:
Чем меньше радиус закругления, тем больше искривлена траектория и тем больше величина нормального ускорения при той же величине скорости. За меру кривизны принимают величину R-1, которую называют кривизной окружности. Очевидно, что ускорение МТ, движущейся по произвольной кривой, также будет зависеть от кривизны траектории, которая различна в разных точках. Найдем ускорение МТ, движущейся по произвольной плоской кривой. Разложим вектор приращения скорости
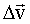 на две составляющие: на две составляющие:
 и и
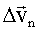 (Рис. 1.2.7). (Рис. 1.2.7).
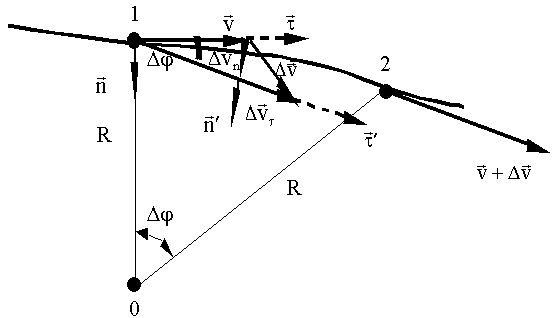
Рис. 1.2.7. К определению полного ускорения
Эти составляющие выберем так, чтобы расстояние от точки 1 до конца вектора
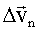 было равно модулю скорости было равно модулю скорости
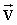 в начальный момент времени. Тогда, очевидно, модуль вектора в начальный момент времени. Тогда, очевидно, модуль вектора  будет равен приращению модуля скорости: будет равен приращению модуля скорости:
Если ввести единичный вектор 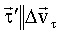 , тогда можно записать: , тогда можно записать:
Для вектора полного ускорения запишем:
Тангенциальное ускорение, учитывая (1.2.29), имеет явный вид:
При переходе к пределу единичный вектор
 совпадет с единичным вектором совпадет с единичным вектором
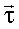 , направленным по касательной к траектории в точке 1 в сторону движения. Этот вектор можно определить так: , направленным по касательной к траектории в точке 1 в сторону движения. Этот вектор можно определить так:
Тогда из (1.2.29), (1.2.31) и (1.2.32) следует:
Итак, вектор полного ускорения равен векторной сумме тангенциального
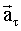 и нормального и нормального
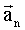 ускорения, первый из которых
( ускорения, первый из которых
(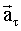 ) направлен по касательной к траектории, а второй ( ) направлен по касательной к траектории, а второй (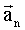 ) перпендикулярен к вектору скорости ) перпендикулярен к вектору скорости 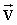 и направлен к центру кривизны траектории (Рис. 1.2.8). и направлен к центру кривизны траектории (Рис. 1.2.8).
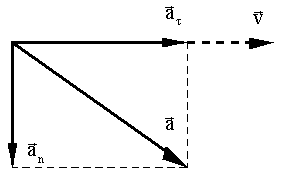
Рис. 1.2.8. Вектор полного ускорения материальной точки
Вектор тангенциального ускорения характеризует изменение скорости по величине. Если скорость не меняется по величине, то тангенциальное ускорение равно нулю и
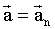 . .
Вектор нормального ускорения 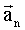 характеризует изменение скорости по направлению. Если направление скорости не изменяется, движение происходит по прямолинейной траектории. Кривизна прямой равна нулю (радиус кривизны равен бесконечности), следовательно, нормальное ускорение равно нулю и выполняется характеризует изменение скорости по направлению. Если направление скорости не изменяется, движение происходит по прямолинейной траектории. Кривизна прямой равна нулю (радиус кривизны равен бесконечности), следовательно, нормальное ускорение равно нулю и выполняется
 . В общем случае модуль вектора полного ускорения равен (Рис. 1.2.8): . В общем случае модуль вектора полного ускорения равен (Рис. 1.2.8):
1.2.5. Кинематика вращательного движения.
Угловые скорости и ускорение
Все точки абсолютно твердого тела, вращающегося вокруг некоторой оси ОО, движутся по окружностям, центры которых лежат на оси вращения. Радиус-вектор каждой точки за время Δt поворачивается на один и тот же угол Δφ. Поворот тела на некоторый угол φ можно задать в виде отрезка, длина которого равна j, а направление совпадает с осью, вокруг которой совершен поворот. Для того чтобы указать, в какую сторону совершается поворот вокруг данной оси, условились связывать направление поворота и изображающего его отрезка так называемым правилом правого винта. Согласно этому правилу, направление отрезка должно быть таким, чтобы, глядя вдоль этого направления, мы видели поворот совершающимся по часовой стрелке (так, как происходит при вращении винта с правой нарезкой резьбы). Векторы, направление которых связывается с направлением вращения, называют аксиальными (в отличие от векторов перемещения, скорости, ускорения, относящихся к полярным векторам).
Величина
является модулем угловой скорости тела. Вектор угловой скорости
 направлен вдоль оси, вокруг которой вращается тело, в сторону, которая определяется правилом правого винта (Рис. 1.2.9). направлен вдоль оси, вокруг которой вращается тело, в сторону, которая определяется правилом правого винта (Рис. 1.2.9).
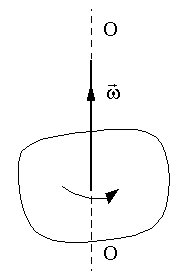
Рис. 1.2.9. Направление вектора угловой скорости твердого тела. ОО - ось вращения
Вращение с постоянной угловой скоростью называется равномерным, при этом
 . Таким образом, при равномерном вращении значение ω показывает, на какой угол поворачивается тело за единицу времени. Равномерное вращение можно характеризовать периодом обращения Т, под которым подразумевается время, за которое тело совершает один полный оборот, т.е. поворачивается на угол φ = 2π. Поэтому выполняется: . Таким образом, при равномерном вращении значение ω показывает, на какой угол поворачивается тело за единицу времени. Равномерное вращение можно характеризовать периодом обращения Т, под которым подразумевается время, за которое тело совершает один полный оборот, т.е. поворачивается на угол φ = 2π. Поэтому выполняется:
откуда:
Число оборотов в единицу времени (частота вращения) равно:
Вектор угловой скорости  может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он изменяется по величине), так и за счет поворота оси - вращения в пространстве (в этом случае изменяется по направлению). Пусть за время Δt вектор может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он изменяется по величине), так и за счет поворота оси - вращения в пространстве (в этом случае изменяется по направлению). Пусть за время Δt вектор  получает приращение получает приращение 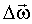 . Изменение вектора угловой скорости со временем характеризуется величиной: . Изменение вектора угловой скорости со временем характеризуется величиной:
которую называют угловым ускорением. Вектор
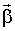 , как и , как и
 , является аксиальным. , является аксиальным.
Когда направление вращения оси в пространстве остается постоянным, угловая скорость изменяется только по величине, следовательно, 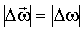 . Используя (1.2.39), получим модуль углового ускорения: . Используя (1.2.39), получим модуль углового ускорения:
Поскольку в этом случае вектор 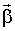 параллелен вектору параллелен вектору  , то формула (1.2.40) может быть записана так: , то формула (1.2.40) может быть записана так:
В этой формуле β - алгебраическая величина, которая положительна, если угловая скорость увеличивается со временем (в этом случае векторы
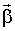 и и
 параллельны), и отрицательна, если угловая скорость уменьшается (направления векторов параллельны), и отрицательна, если угловая скорость уменьшается (направления векторов
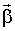 и и
 противоположны). противоположны).
Отдельные точки вращающегося тела имеют различные линейные скорости
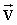 . Скорость каждой из точек, направленная по касательной к соответствующей окружности, непрерывно изменяет свое направление. Покажем, что величина скорости v определяется угловой скоростью вращения тела ω и расстоянием R от рассматриваемой точки тела до оси вращения. Пусть за малый промежуток времени Δt тело повернулось на угол Δφ (Рис. 1.2.10). . Скорость каждой из точек, направленная по касательной к соответствующей окружности, непрерывно изменяет свое направление. Покажем, что величина скорости v определяется угловой скоростью вращения тела ω и расстоянием R от рассматриваемой точки тела до оси вращения. Пусть за малый промежуток времени Δt тело повернулось на угол Δφ (Рис. 1.2.10).
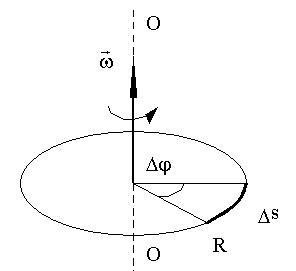
Рис. 1.2.10. К расчету взаимосвязи угловой и линейной скорости. ОО - ось вращения
Точка, находящаяся на расстоянии R от оси вращения, проходит при этом путь Δs, равный
По определению, линейная скорость МТ равна:
Следовательно, взаимосвязь между угловой скоростью вращения тела ω и линейной скоростью МТ имеет вид:
Итак, чем дальше отстоит точка от оси вращения, тем с большей линейной скоростью она движется.
Найдем линейное ускорение точек вращающегося тела. Подставляя в выражение для модуля нормального ускорения (1.2.27) линейную скорость (1.2.44), получим:
Используя выражение для модуля тангенциального ускорения (1.2.33) и (1.2.44), имеем:
Следовательно, между тангенциальным и угловым ускорением есть взаимосвязь:
Таким образом, как нормальное, так и тангенциальное ускорение растет линейно с увеличением расстояния от МТ до оси вращения тела.
Найдем взаимосвязь между векторами
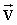 и и
 с помощью векторного произведения. Пусть тело вращается вокруг оси z с угловой скоростью с помощью векторного произведения. Пусть тело вращается вокруг оси z с угловой скоростью
 (Рис. 1.2.11). (Рис. 1.2.11).
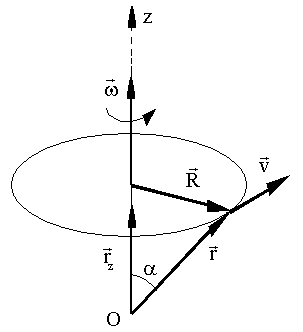
Рис. 1.2.11. Связь между векторами угловой и линейной скорости
Пользуясь определением векторного произведения, видим, что векторное произведение
 на радиус-вектор на радиус-вектор
 представляет собой вектор, совпадающий по направлению с вектором представляет собой вектор, совпадающий по направлению с вектором
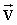 и имеющий модуль, равный и имеющий модуль, равный
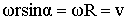 .
Таким образом, векторное произведение .
Таким образом, векторное произведение
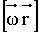 и по направлению, и по модулю равно вектору и по направлению, и по модулю равно вектору
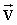 : :
| 

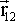 и
и
 , то суммарное перемещение можно задать одним вектором
, то суммарное перемещение можно задать одним вектором
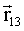 (Рис. 1.2.2, б), который задает такое же перемещение. Результат сложения векторов определяется соотношением:
(Рис. 1.2.2, б), который задает такое же перемещение. Результат сложения векторов определяется соотношением:

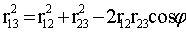
 ,
проведенного из начала координат системы отсчета в МТ. При движении МТ вектор
,
проведенного из начала координат системы отсчета в МТ. При движении МТ вектор


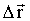 . Возьмем отношение:
. Возьмем отношение: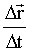
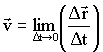
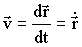

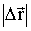 .
Однако, если временной промежуток Δt → 0, то различие между Δs и
.
Однако, если временной промежуток Δt → 0, то различие между Δs и
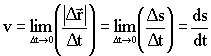

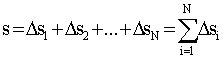

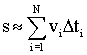
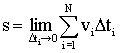
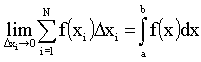
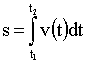


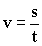
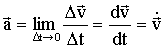
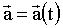 и начальная скорость
и начальная скорость
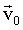 , то можно найти скорость МТ в любой момент времени:
, то можно найти скорость МТ в любой момент времени: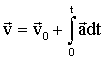

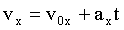
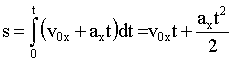

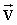 получает приращение
получает приращение
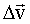 , в результате чего вектор скорости, оставаясь неизменным по величине (при равномерном движении по окружности
, в результате чего вектор скорости, оставаясь неизменным по величине (при равномерном движении по окружности
 ), повернется на угол Δφ, совпадающий по величине с центральным углом, опирающимся на дугу длиной Δs:
), повернется на угол Δφ, совпадающий по величине с центральным углом, опирающимся на дугу длиной Δs:
 параллельно самому себе так, чтобы его начало совпадало с началом вектора
параллельно самому себе так, чтобы его начало совпадало с началом вектора
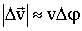
 , тогда можно записать:
, тогда можно записать: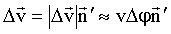
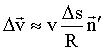
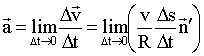
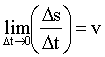 ;
единичный вектор
;
единичный вектор 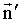 в пределе совпадет с единичным вектором
в пределе совпадет с единичным вектором 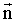 , нормальным к окружности в точке 1 и направленным к центру. Следовательно, можно записать:
, нормальным к окружности в точке 1 и направленным к центру. Следовательно, можно записать: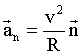
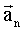 . Модуль нормального ускорения равен:
. Модуль нормального ускорения равен:
 и
и
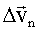 (Рис. 1.2.7).
(Рис. 1.2.7).
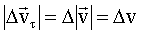
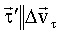 , тогда можно записать:
, тогда можно записать:
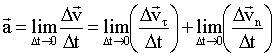
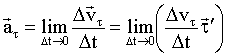
 совпадет с единичным вектором
совпадет с единичным вектором
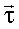 , направленным по касательной к траектории в точке 1 в сторону движения. Этот вектор можно определить так:
, направленным по касательной к траектории в точке 1 в сторону движения. Этот вектор можно определить так: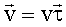

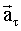 и нормального
и нормального
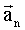 ускорения, первый из которых
(
ускорения, первый из которых
(
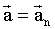 .
. . В общем случае модуль вектора полного ускорения равен (Рис. 1.2.8):
. В общем случае модуль вектора полного ускорения равен (Рис. 1.2.8):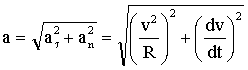
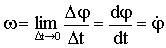
 направлен вдоль оси, вокруг которой вращается тело, в сторону, которая определяется правилом правого винта (Рис. 1.2.9).
направлен вдоль оси, вокруг которой вращается тело, в сторону, которая определяется правилом правого винта (Рис. 1.2.9).
 . Таким образом, при равномерном вращении значение ω показывает, на какой угол поворачивается тело за единицу времени. Равномерное вращение можно характеризовать периодом обращения Т, под которым подразумевается время, за которое тело совершает один полный оборот, т.е. поворачивается на угол φ = 2π. Поэтому выполняется:
. Таким образом, при равномерном вращении значение ω показывает, на какой угол поворачивается тело за единицу времени. Равномерное вращение можно характеризовать периодом обращения Т, под которым подразумевается время, за которое тело совершает один полный оборот, т.е. поворачивается на угол φ = 2π. Поэтому выполняется:
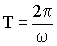

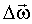 . Изменение вектора угловой скорости со временем характеризуется величиной:
. Изменение вектора угловой скорости со временем характеризуется величиной: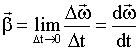
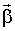 , как и
, как и
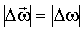 . Используя (1.2.39), получим модуль углового ускорения:
. Используя (1.2.39), получим модуль углового ускорения:
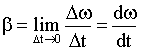

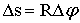

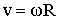
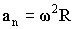
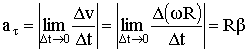
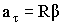

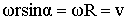 .
Таким образом, векторное произведение
.
Таким образом, векторное произведение
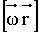 и по направлению, и по модулю равно вектору
и по направлению, и по модулю равно вектору
