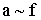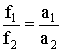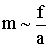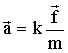МОДУЛЬ 1. Основы механики

ТЕМА 1.3. Динамика материальной точки

1.3.1. Классическая механика и границы ее применимости

1.3.2. Первый закон Ньютона. Инерциальные системы отсчета

1.3.3. Второй закон Ньютона

1.3.4. Единицы измерения и размерности физических величин

1.3.5. Третий закон Ньютона

1.3.6. Импульс. Закон сохранения импульса

Тест 1.3.

1.3.1. Классическая механика
и границы ее применимости

Кинематика дает описание движения тел, не затрагивая вопроса о том, почему тело движется именно так, а не иначе.

Динамика изучает движение тел в связи с их взаимодействиями, которые и обусловливают тот или иной характер движения. В основе классической динамики лежат три закона, сформулированных И.Ньютоном в 1687 г. Эти законы возникли в результате обобщения большого количества опытных фактов.

Ньютоновская механика достигла больших успехов, благодаря чему стали считать, что объяснение любого физического процесса можно свести к законам механики. Однако с развитием науки на рубеже 19-20 веков обнаружились новые факты, которые не укладывались в рамки классической механики, например, независимость скорости света от скорости движения наблюдателя. Объяснение этому явлению было найдено только с помощью теории относительности, развитой А.Эйнштейном в 1905 г. В этой теории подверглись радикальному пересмотру классические представления о пространстве и времени, что привело к созданию релятивистской механики (механики больших скоростей). Однако "отмены" представлений классической механики не произошло, поскольку уравнения релятивистской механики в пределе скоростей, малых по сравнению со скоростью света, переходят в уравнения классической механики. Таким образом, классическая механика вошла в релятивистскую механику как частный случай.

Аналогично обстоит дело и с соотношением между квантовой и классической механиками. Последняя возникла в 20-х годах 20 века в результате развития представлений о строении атома. Движение микрочастиц в атомах и внутри твердых тел уже не подчиняется законам классической механики. Однако для тел с массами, много большими атомных, уравнения квантовой механики также переходят в классические. Следовательно, классическая механика вошла в квантовую механику в качестве частного предельного случая.

1.3.2. Первый закон Ньютона.
Инерциальные системы отсчета

Первый закон Ньютона формулируется так: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.

Оба названных в определении состояния движения характеризуются отсутствием ускорения тела. Поэтому первый закон Ньютона имеет очевидное следствие: скорость любого тела остается постоянной (в частности, равной нулю), пока воздействие на это тело со стороны других тел не вызовет ее изменения.

Полного соответствия первому закону Ньютона реально в природе не существует. В наблюдаемых на практике случаях покоя или равномерного и прямолинейного движения имеют дело с телами, воздействия на которые уравновешивают друг друга. Например, книга, лежащая на столе, испытывает притяжение со стороны Земли, а также давление со стороны стола. Поскольку эти воздействия уравновешивают друг друга, книга покоится.

Первый закон Ньютона выполняется только в определенной системе отсчета. Рассмотрим, например, две системы отсчета, движущиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно будет двигаться с ускорением. Следовательно, первый закон Ньютона не может выполняться одновременно в обеих системах.

Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной. Сам этот закон называют также законом инерции. Система отсчета, в которой не выполняется первый закон Ньютона, называется неинерциальной. Инерциальных систем отсчета (ИСО) существует бесконечное множество. Любая система отсчета, движущаяся некоторой ИСО равномерно и прямолинейно, также будет инерциальной.

Опытным путем из астрономических наблюдений установлено, что система отсчета, центр которой находится в центре Солнца, а оси направлены на выбранные соответствующим образом звезды, является инерциальной. Это - так называемая гелиоцентрическая система отсчета. Земля движется относительно Солнца и звезд по криволинейной траектории, имеющей форму эллипса. Криволинейное движение - это всегда движение с ускорением. Кроме того, Земля вращается вокруг своей оси. Поэтому система отсчета, связанная с поверхностью Земли, движется с ускорением относительно гелиоцентрической системы отсчета и не является инерциальной. Однако ускорение настолько мало, что в большом числе случаев названную систему можно считать инерциальной.

1.3.3. Второй закон Ньютона

Сейчас нам следует выяснить вопрос о влиянии воздействий на данное тело, приводящих к изменению состояний движения, которые определены первым законом Ньютона. Введем новую физическую величину - силу. Сила дает количественную характеристику и направление воздействия, которое производят другие тела на данное тело. Другой важной характеристикой динамики тел является масса - количественная характеристика инерции отклика тела на указанные воздействия.

Воздействие, производимое на тело, может приводить как к изменению скорости тела, так и к его деформации. Оба этих эффекта - и ускорение, и деформация - могут быть измерены и служить для количественной характеристики воздействий.

Рассмотрим такой эксперимент. К пружине, закрепленной верхним концом на опоре, подвешивают груз. Под воздействием груза и опоры, к которой прикреплена пружина, последняя получит некоторое удлинение. Удваивая груз, можно убедиться, что удлинение пружины также увеличится вдвое. Три равных груза вызовут утроенную деформацию и т.д. Следовательно, при упругой деформации пружины выполняется закон Гука: удлинение пружины при не слишком больших деформациях прямо пропорционально действующей на нее силе.

Таким образом, проградуировав удлинение пружины, можно измерить силу, действующую на тело.

Простой опыт установления второго закона Ньютона состоит в следующем. Пусть тележка движется по горизонтальной плоскости под воздействием натяжения нити, переброшенной через блок с прикрепленным к ней определенным грузом. Для измерения силы натяжения используется проградуированная пружина, которую следует вставить между тележкой и нитью. Направление воздействия задается направлением нити. Подвешивая разные грузы, можно варьировать силу, под действием которой происходит движение.

При постоянном натяжении нити (одном и том же грузе) тележка движется равномерно-ускоренно, причем ускорение прямо пропорционально приложенной силе:

(1.3.1)

Естественно, что результат (1.3.1) будет выполняться тем точнее, чем меньше сила трения колес с осями и плоскостью движения. Соотношение (1.3.1) для двух разных сил будет иметь вид пропорции:

(1.3.2)

Если взять тележку с другой массой, то, хотя качественно зависимость (1.3.1) сохраняется, ускорение тележки при той же действующей силе будет другим. Оказалось, что при любой по величине и направлению силе отношение ее величины к ускорению, возникающему под действием данной силы, остается постоянным для данного тела. Тем самым величина отношения f/a характеризует инертность данного тела. Поэтому для количественной характеристики инертности тела применяется пропорциональная данному отношению физическая величина, получившая название массы тела m:

(1.3.3)

Запишем соотношение (1.3.3) в виде:

(1.3.4)

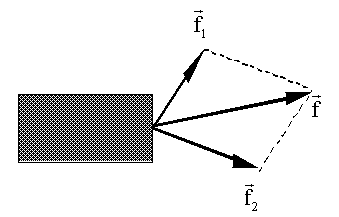
где k - коэффициент пропорциональности. Эта формула представляет собой аналитическое выражение второго закона Ньютона.

Итак, второй закон Ньютона формулируется следующим образом: ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела. И первый, и второй законы Ньютона справедливы только в инерциальных системах отсчета.

В частном случае, когда сила равна нулю (при отсутствии воздействия на тело других тел), ускорение также равно нулю. Этот случай сводится к первому закону Ньютона. Однако важность первого закона Ньютона состоит также в том, что в нем содержится постулат о существовании ИСО.

Сила имеет векторный характер. Непосредственным опытным путем (Рис. 1.3.1) можно показать, что результатом действия двух сил, приложенных к одной и той же точке тела под углом друг к другу, будет равнодействующая сила, которую можно определить по правилу параллелограмма.

Рис. 1.3.1. Векторное сложение сил

Направление действия силы и ускорение совпадают по направлению, притом, что масса - это скалярная величина, поэтому в векторном виде соотношение (1.3.4) можно представить так:

(1.3.5)

Уравнение (1.3.5) - это основное уравнение классической механики.

1.3.4. Единицы измерения
и размерности физических величин

Законы физики устанавливают количественные соотношения между физическими величинами. Для этого последние необходимо уметь измерять. Измерить какую-либо физическую величину означает сравнить ее с величиной того же вида, принятой за единицу.

Оказалось, что можно ограничиться выбором единиц измерения для трех основных величин, приняв их за основные. Единицы измерения всех прочих величин можно установить, пользуясь физическими законами, которые связывают такие величины с основными.

Например, пусть уже установлены единицы измерения для массы и ускорения. Выберем в соотношении (1.3.5) коэффициент пропорциональности равным единице. Тогда это соотношение принимает более простой вид:

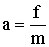(1.3.6)

Из (1.3.6) следует, что единица силы представляет собой такую величину, под действием которой тело с массой, равной единице, приобретает ускорение, равное единице.

Существует несколько систем, отличающихся выбором основных единиц. Системы, в основу которых положены единицы длины, массы и времени, называются абсолютными. В нашей стране применяется Международная система единиц (СИ). Основными единицами СИ являются: единица длины - метр (м), единица массы - килограмм (кг), единица времени - секунда (с). Кроме указанных, в СИ принимают в качестве основных: единица силы тока - ампер (А), единица термодинамической температуры - градус Кельвина (К), единица силы света - кандела (кд).

Метр определяется как длина, равная 1650763,73 длин волн излучения, соответствующего переходу между уровнями 2р₁₀ и 5d₅ атома криптона ⁸⁶Cr (оранжевая линия). Метр приближенно равен 1/40000000 доле длины земного гринвичского меридиана. Применяются кратные и дольные единицы.

Масса - это единственная основная единица, связанная с существованием искусственно созданного материального прототипа. Прототип 1 кг массы представляет собой находящийся в Международном бюро мер и весов в севре под Парижем цилиндр из сплава платины (90%) и иридия (10%) диаметром 39 мм и такой же высоты. Выбор этого сплава обеспечивает твердость, стойкость, однородность и высокую полируемость поверхности эталона. Масса прототипа близка к массе 1000 см³ чистой воды при 4°С. В одном килограмме содержится 1000 грамм (г).

Секунда определяется из астрономических измерений как 1/315556925,9747 часть тропического года. Секунда приблизительно равна 1/86400 средних солнечных суток.

В физике применяется также абсолютная система единиц, называемая СГС. Основными единицами в ней являются сантиметр, грамм и секунда.

Единицы измерения скорости и ускорения являются производными (м/с и м/с², соответственно).

Единицей измерения силы в СИ является 1 Ньютон (Н). Единица силы в СГС - дина (дин). Между 1 Н и 1 дин есть соотношение:

Существует также техническая система единиц МКГСС. Основные единицы - метр, секунда и единица силы - килограмм-сила (кгс или кГ). Килограмм-сила определяется как сила, которая сообщает телу с массой 1 кг ускорение, равное 9,80655 м/с². Отсюда 1 кГ = 9,80655 Н.

Для обозначения размерности физической величины используется ее буквенное обозначение, взятое в квадратные скобки. Для размерностей основных величин используют специальные обозначения:

Поскольку физические законы не могут зависеть от выбора единиц измерения входящих в них величин, размерности обеих частей уравнений, выражающих эти законы, должны быть одинаковы. Это обстоятельство может быть использовано, во-первых, для проверки правильности полученных физических соотношений и, во-вторых, для установления размерностей физических величин. Например, скорость определяется формулой v = Δs / Δt. Размерность [Δs] = L, [Δt] = T, поэтому размерность правой части [Δs] / [Δt] = L/T = LT^-1. Поэтому размерность скорости [v] = LT^-1.

1.3.5. Третий закон Ньютона

Всякое действие тел друг на друга имеет характер взаимодействия: если тело М₁ действует на тело М₂ с некоторой силой 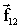, то и тело М₂ действует на тело М₁ с силой 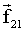. Обе силы совершенно равноправны. Под действием этих сил тела приобретают ускорения и 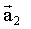соответственно. Величины этих ускорений оказываются обратно пропорциональными массам тел:

(1.3.7)

откуда следует, что m₁a₁ = m₂a₂ и, следовательно, равенство сил f₁₂ = f₂₁. Направления сил, очевидно, противоположны. Поэтому третий закон Ньютона следует сформулировать так: всякое действие тел друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга взаимодействующие тела, всегда равны по величине и противоположны по направлению.

Формально содержание третьего закона Ньютона имеет вид:

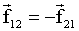(1.3.8)

Из сказанного следует, что силы всегда возникают попарно: всякой силе, приложенной к какому-либо телу, можно сопоставить равную ей по величине и противоположно направленную силу, приложенную к другому телу, взаимодействующему с данным.

Третий закон Ньютона - закон взаимодействия тел и применяется при анализе столкновений и рассеяния тел. Указанные силы возникают только при непосредственном силовом взаимодействии тел.

1.3.6. Импульс. Закон сохранения импульса

Уравнение второго закона Ньютона

(1.3.9)

можно представить в другом виде:

поскольку масса тела от времени не зависит. Введя векторную величину - импульс МТ:

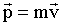(1.3.10)

уравнение динамики (1.3.9) можно записать так:

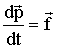(1.3.11)

Тогда второй закон Ньютона можно сформулировать так: производная импульса материальной точки по времени равна результирующей всех сил, действующих на точку.

Умножив (1.3.11) на dt, получим:

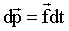(1.3.12)

Интегрируя (1.3.12), имеем приращение импульса за промежуток времени от t₁ до t₂:

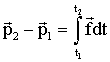(1.3.13)

Если сила от времени не зависит, то приращение импульса за промежуток времени t равно

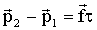Рассмотрим систему, состоящую из N материальных точек. Тела, входящие в систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. Будем называть внутренними силы, с которыми на данное тело действуют остальные тела системы, внешними - силы, обусловленные воздействием тел, не принадлежащих системе. В случае, когда внешние силы отсутствуют, система МТ называется замкнутой.

Импульсом системы называется векторная сумма импульсов тел данной системы:

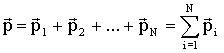(1.3.14)

Назовем центром инерции системы точку, положение которой в пространстве задается радиус-вектором:

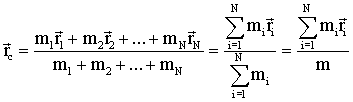(1.3.15)

где m_i - масса i-го тела,

m - масса системы,

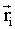- радиус-вектор, определяющий положение i-го тела.

Положение центра инерции в теле совпадает с центром тяжести (в однородном поле силы тяжести).

Скорость центра инерции получается путем дифференцирования (1.3.15) по времени:

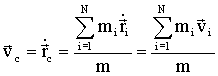(1.3.16)

Учитывая, что 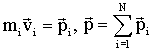- импульс системы МТ, можно записать:

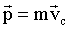(1.3.17)

Следовательно, импульс системы равен произведению массы системы на скорость ее центра инерции.

Пусть система МТ состоит из трех тел (Рис. 1.3.2).

Рис. 1.3.2. Система трех тел

Напишем для каждого из трех тел уравнение динамики:

(1.3.18)

Здесь f_i - внешние силы, действующие на каждое из трех тел системы. Согласно третьему закону Ньютона, выполняется: . Складывая уравнения (1.3.18), видим, что сумма внутренних сил равна нулю, вследствие чего имеем:

(1.3.19)

При отсутствии внешних сил из (1.3.19) следует:

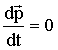(1.3.20)

Следовательно, для замкнутой системы импульс не зависит от времени (сохраняется). Это утверждение можно обобщить и на случай N тел. Тогда можно сформулировать закон сохранения импульса: импульс замкнутой системы материальных точек остается постоянным.

Импульс замкнутой системы материальных точек остается постоянным и в случае, когда силы, воздействующие на систему, в сумме равны нулю.

Из закона сохранения импульса следует, что центр инерции замкнутой системы тел либо движется равномерно и прямолинейно, либо остается неподвижным. Существует много явлений, в основе которых лежит закон сохранения импульса. Например, находясь на скользком полу, невозможно сдвинуть с места какой-либо предмет, без того, чтобы самому не начать скользить в противоположном направлении. Действие ракет и реактивных двигателей основано на том, что в результате выбрасывания из сопла ракеты струи образовавшихся при сгорании топлива газов ракете сообщается такой же по величине импульс, какой уносят с собой газы.