где α - угол между направлением векторов силы и перемещения тела. Если сила и перемещение образуют острый угол, то cosα > 0, и работа положительна. Если угол α - тупой, то cosα < 0, и работа отрицательна. При α = π/2 работа равна нулю. Если величина проекции силы на направление перемещения не остается постоянной во время движения, для вычисления работы следует разбить путь s на элементарные участки Δs, взяв их столь малыми, чтобы за время прохождения телом такого участка величину проекции силы можно было считать практически постоянной. Тогда работа силы на каждом элементарном участке приближенно равна.
а работа на всем пути s может быть вычислена как сумма элементарных работ.
Устремляя Δsi к нулю, получим, что приближенное равенство (1.4.3) перейдет в точное значение.
Из Рис. 1.4.1 видно, что элементарная работа (в координатах "сила - путь") численно равна площади заштрихованной фигуры, а работа А на пути от точки 1 к точке 2 численно равна площади фигуры, ограниченной кривой силы fs и вертикальными прямыми 1 и 2 и осью s.
Найдем работу, совершаемую при растяжении пружины. Считаем, что растяжение происходит в соответствии с законом Гука. Растяжение производится медленно, чтобы силу, которая действует на пружину, можно было все время считать равной по величине упругой силе f = kx (х - удлинение пружины при растяжении). Путь, проходимый точкой приложения силы, равен х (Рис. 1.4.2). Тогда из Рис. 1.4.2 следует, что работа, которую нужно совершить, чтобы деформировать пружину, удлинив ее на величину х, равна.
При сжатии пружины на величину х совершается такая же по величине и знаку работа, что и при растяжении, поскольку отрицательны и проекция силы, и растяжение. Работа упругой силы (силы, действующей со стороны пружины на деформирующее ее тело) и при растяжении, и при сжатии равна (-kx2/2), так как упругая сила в любой момент времени равна по величине, но противоположна по направлению силе, вызывающей деформацию пружины. В качестве единицы работы выбирают работу силы, равной единице, действующей в направлении перемещения, на пути, равном единице. В системе СИ - 1 Джоуль (Дж), в СГС - 1 эрг (1 эрг = 1 дин · 1 см). 1 Дж = 1 Н · 1 м = 105 дин · 102 см = 107 эрг. Выражение для работы может быть представлено в виде скалярного произведения вектора силы на вектор перемещения.
1.4.2. МощностьНа практике имеет значение не только величина совершенной работы, но и время, в течение которого она совершается. Поэтому вводят величину, которая называется мощностью и показывает, какую работу данный механизм совершает в единицу времени.
Если за одинаковые промежутки времени совершается различная работа, мощность также меняется во времени. Поэтому вводят понятие мгновенной мощности.
Пусть за время dt точка приложения силы приобретает перемещение
Следовательно, мощность оказывается равной скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения силы. За единицу мощности принимается такая величина, при которой за единицу времени совершается работа, равная единице. В СИ единицей мощности является 1 Ватт (Вт) = 1 Дж/сек, в СГС - 1 эрг/сек. 1 Вт = 107 эрг/сек. В рационализированной МКГСС системе единицей мощности является лошадиная сила (л.с.). 1 л.с. = 75 кГ·м/сек = 736 Вт. 1.4.3. Потенциальное поле сил.
|
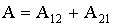 | (1.4.10) |
Рассмотрим участок траектории, показанной на Рис. 1.4.3 (Рис. 1.4.4).

Рис. 1.4.4. К расчету работы консервативных сил в потенциальном поле
Поскольку в потенциальном поле сила
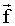 зависит только от положения тела в пространстве и не зависит от состояния движения тела, элементарная работа на пути Δs при движении в одном направлении равна
зависит только от положения тела в пространстве и не зависит от состояния движения тела, элементарная работа на пути Δs при движении в одном направлении равна
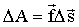 ,
при движении в другом направлении она равна
,
при движении в другом направлении она равна
 . Так как
. Так как
 , то
, то
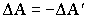 . Это справедливо для любого элементарного участка пути, так что выполняется.
. Это справедливо для любого элементарного участка пути, так что выполняется.
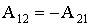 | (1.4.11) |
Подставляя (1.4.11) в (1.4.10), получим, что работа по перемещению тела по замкнутой траектории в потенциальном поле равна нулю.
Если работа каких-либо сил на любом замкнутом пути равна нулю, то работа этих сил при переходе тела из одного положения в другое также не зависит от пути. Поэтому потенциальное поле сил можно определить как поле таких сил, работа которых на любом замкнутом пути равна нулю. Поскольку работа в потенциальном поле сил на замкнутом пути равна нулю, на одних участках замкнутого пути силы совершают положительную работу, на других - отрицательную. Работа сил трения за промежуток времени Δt равна.
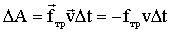 | (1.4.12) |
поскольку сила трения направлена в сторону, противоположную скорости. Следовательно, работа сил трения все время остается отрицательной и на замкнутом пути будет отличаться от нуля. Таким образом, силы трения относятся к числу неконсервативных сил.
Докажем, что поле сил тяжести является потенциальным. Сила, действующая на тело в любой точке траектории, имеет одинаковую величину P = mg и направлена вертикально вниз. Поэтому работа равна.
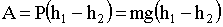 | (1.4.13) |
Очевидно, что это выражение не зависит от пути, откуда следует, что поле сил тяжести является потенциальным.
1.4.4. Энергия. Кинетическая и потенциальная энергия.
Закон сохранения энергии
Тела часто оказываются в состоянии совершать работу над другими телами. Физическая величина, характеризующая способность тела или системы тел совершать работу, называется энергией. Энергия тела в механике может иметь двоякую природу.
- возникать вследствие движения тела (кинетическая энергия, или энергия движущегося тела);
- возникать вследствие пребывания тела в потенциальном поле сил (потенциальная энергия - энергия положения тела).
Кинетическая энергия
Пусть тело 1 с массой m, движущееся со скоростью
 , действует с силой
, действует с силой
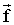 на соприкасающееся с ним тело 2 (Рис. 1.4.5).
на соприкасающееся с ним тело 2 (Рис. 1.4.5).

Рис. 1.4.5. К определению кинетической энергии
За время dt точка приложения силы получит перемещение
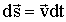 ,
вследствие чего тело 1 совершит над телом 2 работу.
,
вследствие чего тело 1 совершит над телом 2 работу.
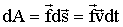 | (1.4.14) |
Очевидно, что в данном случае тело 1 совершает работу над другим телом за счет запаса энергии, которой оно обладало вследствие своего движения, т.е. запаса кинетической энергии Т (если бы тело 1 не двигалось, было бы равно нулю перемещение тела 2, и работа также была бы равной нулю). Поэтому совершенную телом 1 работу можно приравнять убыли его кинетической энергии.
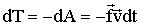 | (1.4.15) |
Согласно третьему закону Ньютона, тело 2 действует на тело 1 с силой
 ,
вследствие чего скорость тела 1 получает за время dt приращение.
,
вследствие чего скорость тела 1 получает за время dt приращение.
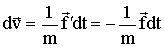 | (1.4.16) |
Умножив скалярно обе части равенства (1.4.16) на
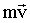 , получим.
, получим.
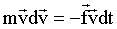 | (1.4.17) |
Сравнивая (1.4.17) с (1.4.15), имеем.
 | (1.4.18) |
Скалярное произведение можно представить в виде:
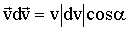 , где dv - приращение модуля скорости (Рис. 1.4.6)
, где dv - приращение модуля скорости (Рис. 1.4.6)
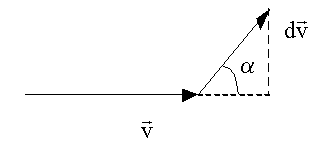
Рис. 1.4.6. К определению кинетической энергии
Поэтому выражение (1.4.18) можно представить так.
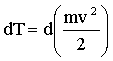 | (1.4.19) |
Отсюда следует, что кинетическая энергия МТ массы m, движущаяся со скоростью v, равна.
 | (1.4.20) |
Умножив числитель и знаменатель этого выражения на m, получим.
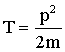 | (1.4.21) |
где p - импульс МТ.
Потенциальная энергия
В самом общем смысле потенциальная энергия - это энергия взаимодействия тел внутри некоторой системы, или энергия взаимодействия частей одного и того же тела. Рассмотрим тело (имеется в виду МТ), находящееся в потенциальном поле сил. Сопоставим каждой точке поля, характеризуемой радиус-вектором
 , определенное значение функции
, определенное значение функции
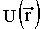 . Для этого в некоторой исходной точке 0 примем произвольное значение этой функции, равное U0. Чтобы получить значение функции, равное U1 в некоторой точке 1, прибавим к U0 работу А10, которую совершают над телом силы поля при перемещении тела из точки 1 в точку 0.
. Для этого в некоторой исходной точке 0 примем произвольное значение этой функции, равное U0. Чтобы получить значение функции, равное U1 в некоторой точке 1, прибавим к U0 работу А10, которую совершают над телом силы поля при перемещении тела из точки 1 в точку 0.
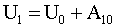 | (1.4.22) |
Поскольку работа в потенциальном поле сил не зависит от пути, найденное таким образом значение U1 оказывается однозначным. Аналогично определяются значения
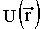 для всех остальных точек поля. В частности, значение
для всех остальных точек поля. В частности, значение
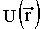 в точке 2 равно.
в точке 2 равно.
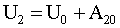 | (1.4.23) |
Вычислим разность U1 - U2. Вычтем (1.4.23) из (1.4.22) и воспользуемся тем, что А20 = –А02. В результате имеем.
 | (1.4.24) |
Сумма А10 + А02 - это работа, совершаемая силами поля при перемещении тела из точки 1 в точку 2 через точку 0. Однако работа при перемещении тела из точки 1 в точку 2 по любой другой траектории (в том числе и не проходящей через точку 0) будет той же самой. Поэтому сумму А10 + А02 можно записать просто в виде А12. В итоге приходим к соотношению.
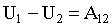 | (1.4.25) |
Следовательно, с помощью функции 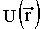 можно определить работу, совершаемую силами поля над телом на любом пути, начинающемся в произвольной точке 1 и заканчивающемся в произвольной точке 2. Эта работа равна убыли функции
можно определить работу, совершаемую силами поля над телом на любом пути, начинающемся в произвольной точке 1 и заканчивающемся в произвольной точке 2. Эта работа равна убыли функции
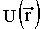 на пути 1 - 2. Тем самым физическую величину
на пути 1 - 2. Тем самым физическую величину
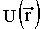 трактуют как один из видов механической энергии - потенциальную энергию.
трактуют как один из видов механической энергии - потенциальную энергию.
Конкретный вид функции 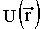 зависит от характера силового поля. Например, в поле сил тяжести вблизи поверхности Земли потенциальная энергия тела имеет вид.
зависит от характера силового поля. Например, в поле сил тяжести вблизи поверхности Земли потенциальная энергия тела имеет вид.
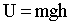 | (1.4.26) |
где h - высота, отсчитанная от уровня, для которого принято U = 0.
Поскольку начало отсчета U можно выбирать произвольно, потенциальная энергия может иметь отрицательные значения. Если, например, принять за нуль потенциальную энергию тела, находящегося на поверхности Земли, то потенциальная энергия тела, лежащего на дне ямы глубиной h', будет равна U = - mgh' (Рис. 1.4.7). Отметим, что кинетическая энергия отрицательной быть не может.

Рис. 1.4.7. Потенциальная энергия поля силы тяжести
Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело. В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела, например, от расстояния между соседними витками пружины.
Как для сжатия, так и для растяжения пружины на величину х необходимо затратить работу
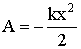 . Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид (Рис. 1.4.8).
. Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид (Рис. 1.4.8).
 | (1.4.27) |
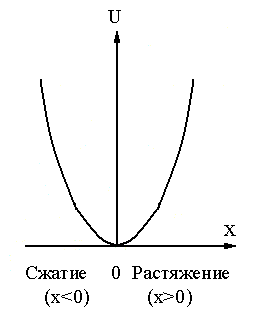
Рис. 1.4.8. Потенциальная энергия сжатия и растяжения пружины
Полная механическая
энергия системы тел
В общем случае тело может обладать одновременно и кинетической и потенциальной энергией. Их сумма образует полную механическую энергию. Например, тело М, находящееся на высоте h над поверхностью Земли и движущееся относительно Земли со скоростью v, обладает полной энергией.
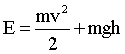 | (1.4.28) |
Потенциальная и кинетическая энергии могут превращаться друг в друга. Рассмотрим случай свободного падения первоначально покоившегося тела с высоты h. До начала падения кинетическая энергия тела равна нулю, потенциальная - равна mgh. В конце падения тело будет обладать скоростью:
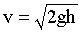 | (1.4.29) |
и, следовательно, кинетической энергией.
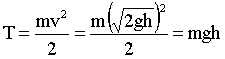 | (1.4.30) |
но зато потенциальная энергия на высоте h = 0 будет равна нулю. Таким образом, потенциальная энергия превращается в эквивалентное количество кинетической энергии.
Тело, брошенное с поверхности Земли вертикально вверх со скоростью v, обладает вначале энергией
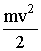 и потенциальной энергией, равной нулю. Постепенно теряя скорость, тело может подняться на высоту h, связанную с начальной скоростью соотношением (1.4.29). На высоте h скорость, а, следовательно, и кинетическая энергия, будет равна нулю, но зато его потенциальная энергия станет равной первоначальному запасу кинетической энергии.
и потенциальной энергией, равной нулю. Постепенно теряя скорость, тело может подняться на высоту h, связанную с начальной скоростью соотношением (1.4.29). На высоте h скорость, а, следовательно, и кинетическая энергия, будет равна нулю, но зато его потенциальная энергия станет равной первоначальному запасу кинетической энергии.
В обоих случаях полная энергия тела остается неизменной (сопротивлением воздуха пренебрегаем). На любой промежуточной высоте h'(0 < h' < h) выполняется.
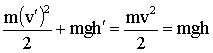 | (1.4.31) |
где v' - скорость тела на промежуточной высоте h'. Полученные соотношения справедливы при отсутствии действия внешних сил.
Если рассматривать систему тел (i = 1, 2, 3,…, N), то для нее полную механическую энергию следует представить в виде.
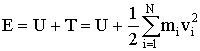 | (1.4.32) |
где mi, vi - массы и скорости тел, входящих в общую систему. Если между телами действуют только консервативные силы, то работа, совершаемая такими силами над любым из тел, не зависит от пути, а определяется только начальным и конечным положением тела в пространстве. В этом случае поле сил является потенциальным. При условии наличия внешних сил происходит приращение полной механической энергии системы тел, равное работе А внешних сил, приложенных к телам системы.
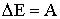 | (1.4.33) |
Если система замкнута, т.е. внешние силы отсутствуют, то ΔЕ = 0, следовательно, выполняется.
 | (1.4.34) |
Соотношения (1.4.33) и (1.4.34) заключают в себе сущность одного из основных законов механики - закона сохранения энергии: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной.
Если в замкнутой системе, кроме консервативных, действуют также неконсервативные силы (например, силы трения), то полная механическая энергия системы не сохраняется. Рассматривая неконсервативные силы как внешние, можем записать.
 | (1.4.35) |
где Aнк - работа неконсервативных сил. Силы трения совершают, как правило, отрицательную работу. Поэтому наличие сил трения в замкнутой системе приводит к уменьшению ее полной механической энергии со временем. Действие сил трения приводит к превращению механической энергии в другие - немеханические виды энергии. В этом случае выполняется более общий закон сохранения: в изолированной от любых внешних воздействий системе сохраняется постоянной сумма всех видов энергии, включая немеханические.
1.4.5. Связь между потенциальной энергией и силой
Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы  , действующей на тело, с другой стороны, некоторое значение потенциальной энергии U. Следовательно, между силой и потенциальной энергией должна существовать определенная взаимосвязь. Чтобы ее установить, вычислим элементарную работу ΔA, совершаемую силами поля при малом перемещении тела Δs, происходящем вдоль произвольно выбранного направления в пространстве (Рис. 1.4.9).
, действующей на тело, с другой стороны, некоторое значение потенциальной энергии U. Следовательно, между силой и потенциальной энергией должна существовать определенная взаимосвязь. Чтобы ее установить, вычислим элементарную работу ΔA, совершаемую силами поля при малом перемещении тела Δs, происходящем вдоль произвольно выбранного направления в пространстве (Рис. 1.4.9).

Рис. 1.4.9. К связи между силой и потенциальной энергией
Эта работа равна.
 | (1.4.36) |
где fs - проекция силы на направление s.
Поскольку работа совершается за счет запаса потенциальной энергии, она равна убыли потенциальной энергии -ΔU на отрезке Δs.
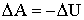 | (1.4.37) |
Тогда из (1.4.36) и (1.4.37) следует.
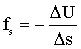 | (1.4.38) |
Чтобы получить значение fs в данной точке, нужно сделать предельный переход:
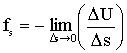 | (1.4.39) |
Поскольку U может изменяться не только при перемещении вдоль оси s, но также и при перемещениях вдоль других направлений, предел в формуле (1.4.39) имеет смысл частной производной.
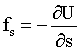 | (1.4.40) |
Соотношение (1.4.40) справедливо для любого направления в пространстве, в частности, и для направлений вдоль декартовых координатных осей.
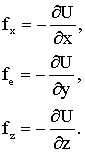 | (1.4.41) |
Если известны эти проекции, то можно определить и вектор силы.
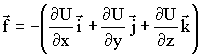 | (1.4.42) |
Математический смысл вектора вида 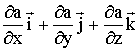 , где а - любая скалярная функция а = а(x, y, z) - это градиент функции а(x, y, z). Вектор градиента показывает изменение величины, а в трехмерном пространстве. Следовательно, сила равна градиенту потенциальной энергии, взятому с обратным знаком.
, где а - любая скалярная функция а = а(x, y, z) - это градиент функции а(x, y, z). Вектор градиента показывает изменение величины, а в трехмерном пространстве. Следовательно, сила равна градиенту потенциальной энергии, взятому с обратным знаком.
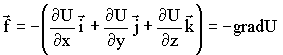 | (1.4.43) |
1.4.6. Условия равновесия механической системы
В замкнутой системе полная энергия остается постоянной, поэтому кинетическая энергия может возрастать только за счет уменьшения потенциальной энергии. Если система находится в таком состоянии, что скорости всех тел равны нулю, а потенциальная энергия имеет минимальное значение, то без воздействия извне тела системы не могут прийти в движение, т.е. система будет находиться в равновесии.
Таким образом, для замкнутой системы равновесной может быть только такая конфигурация тел, которая соответствует минимуму потенциальной энергии. Рассмотрим случай, когда взаимное расположение тел системы определяется только одной координатой х. В качестве примера можно привести систему Земля-шарик, скользящий без трения по неподвижно укрепленной изогнутой проволоке (Рис.1.4.10). Другой пример – прикрепленный к концу пружины шарик, скользящий по горизонтальной направляющей (Рис.1..4.11). Графики функции U(x) показаны на этих же рисунках. Минимумам U(x0) соответствуют значения х = x0. Условие минимума U(x) имеет вид:
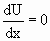 . . | (1.4.44) |
Тогда из (3.41) следует, что:
| fx = 0. | (1.4.45) |
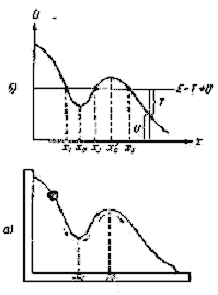 | 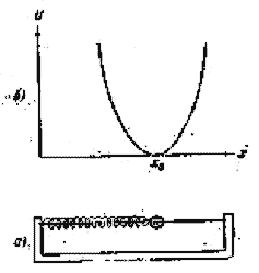 |
| Рис.1.4.10. Движение шарика в поле силы тяжести по специальной траектории | Рис.1.4.11. Движение шарика в поле упругих сил пружины |
Таким образом, конфигурация системы, соответствующая минимуму потенциальной энергии, обладает тем свойством, что силы, действующие на тела системы, равны нулю. Этот результат остается справедливым и для случая, когда потенциальная энергия является функцией нескольких переменных. В случае, когда шарик (Рис.1.4.10б) находится в положении 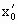 , условия (1.4.44) и (1.4.45) также выполняются. Это положение соответствует максимуму потенциальной энергии. Однако такое равновесие будет неустойчивым: достаточно слегка вывести шарик из этого положения, как возникает сила, которая будет удалять шарик от положения
, условия (1.4.44) и (1.4.45) также выполняются. Это положение соответствует максимуму потенциальной энергии. Однако такое равновесие будет неустойчивым: достаточно слегка вывести шарик из этого положения, как возникает сила, которая будет удалять шарик от положения  . Силы, возникающие при смещении шарика из положения устойчивого равновесия х = х0, направлены так, что стремятся вернуть шарик в положение равновесия.
. Силы, возникающие при смещении шарика из положения устойчивого равновесия х = х0, направлены так, что стремятся вернуть шарик в положение равновесия.
Рис.1.4.11 б, поясняет, как с помощью графика U определить кинетическую энергию, которой обладает система при данном значении x.
1.4.7. Центральный удар шаров
При соударении тел друг с другом они претерпевают деформации. Кинетическая энергия, которой обладали тела до соударения, частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел. Увеличение внутренней энергии тел сопровождается увеличением их температуры.
Существуют два предельных типа соударений: абсолютно упругий и абсолютно неупругий. Абсолютно упругим называется такой удар, при котором механическая энергия не переходит в другие (немеханические) виды энергии. При таком ударе кинетическая энергия полностью переходит в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию, и тела разлетаются со скоростями, величина и направление которых определяются двумя условиями: сохранением полной энергии и сохранением полного импульса.
Абсолютно неупругим называется такой удар, который характеризуется тем, что потенциальной энергии упругой деформации не возникает; кинетическая энергия тел полностью превращается во внутреннюю энергию тел. После удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполняется лишь закон сохранения полного импульса, закон сохранения механической энергии не соблюдается – имеет место закон сохранения суммарной энергии различных видов (механической и внутренней).
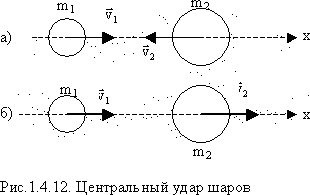
Ограничимся рассмотрением центрального удара двух шаров. Удар называется центральным, если шары до удара двигались вдоль прямой, проходящей через их центры. При центральном ударе соударение может произойти в случаях:
- шары движутся навстречу друг другу;
- один из шаров догоняет другой (Рис.1.4.12).
Будем считать, что шары образуют замкнутую систему, или что внешние силы, приложенные к шарам, уравновешивают друг друга.
Абсолютно неупругий удар.
Пусть массы шаров равны m1 и m2, а скорости до удара -  и
и 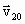 . В силу закона сохранения полного импульса суммарный импульс шаров после удара должен быть таким же, как и до удара:
. В силу закона сохранения полного импульса суммарный импульс шаров после удара должен быть таким же, как и до удара:
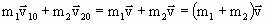 , , | (1.4.46) |
где  - одинаковая для обоих шаров скорость после удара. Из (1.4.46) следует, что:
- одинаковая для обоих шаров скорость после удара. Из (1.4.46) следует, что:
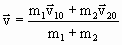 . . | (1.4.47) |
Поскольку векторы  и
и 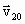 направлены вдоль одной прямой, вектор
направлены вдоль одной прямой, вектор  имеет то же направление. Модуль этого вектора можно вычислить по следующей формуле:
имеет то же направление. Модуль этого вектора можно вычислить по следующей формуле:
 . . | (1.4.48) |
Знак «минус» соответствует случаю а), знак «+» – случаю б) на Рис.1.4.12. Кинетические энергии системы до удара и после удара (случай Рис.1.4.12а) равны соответственно:
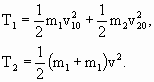 | (1.4.49) |
Разница этих значений дает величину:
 , , | (1.4.50) |
где  - приведенная масса шаров. Таким образом, при абсолютно неупругом столкновении двух шаров происходит потеря кинетической энергии движения, равная половине произведения приведенной массы на квадрат относительной скорости. Именно эта доля кинетической энергии идет на увеличение внутренней энергии тел (на их нагревание).
- приведенная масса шаров. Таким образом, при абсолютно неупругом столкновении двух шаров происходит потеря кинетической энергии движения, равная половине произведения приведенной массы на квадрат относительной скорости. Именно эта доля кинетической энергии идет на увеличение внутренней энергии тел (на их нагревание).
Абсолютно упругий удар.
При таком ударе выполняются два закона: сохранения механической энергии и сохранения механического импульса. Пусть массы шаров равны m1 и m2, скорости до удара -  и
и 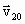 , скорости после удара -
, скорости после удара -  и
и ![]() . Напишем уравнения сохранения механического импульса и сохранения механической энергии:
. Напишем уравнения сохранения механического импульса и сохранения механической энергии:
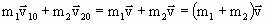 , , | (1.4.51) |
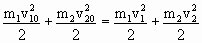 . . | (1.4.52) |
Преобразуем (1.4.51) так:
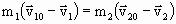 . . | (1.4.53) |
Соотношение (1.4.53) можно представить в виде:
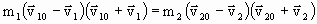 . . | (1.4.54) |
Исходя из симметрии задачи можно считать, что скорости шаров после удара будут направлены вдоль той же прямой, вдоль которой двигались центры шаров до удара. Следовательно, все векторы в (1.4.53) и (1.4.54) коллинеарны. Подставляя (1.4.53) в (1.4.54), получим:
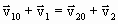 . . | (1.4.55) |
Умножая (1.4.54) на m2 и вычитая это значение из (1.4.53), а затем умножая (1.4.55) на m1 и складывая с (1.4.53), получим:
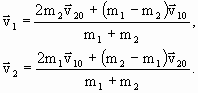 | (1.4.56) |
Для численных расчетов используем выражения для модулей скоростей:
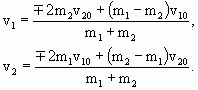 | (1.4.57) |
Знак «минус» соответствует случаю а) шары движутся навстречу; знак «+» – случаю б) шары движутся один за другим (Рис.1.4.12).
Рассмотрим случай, когда массы соударяющихся шаров равны: m1 = m2 = m. Из (1.4.57) следует, что при этом выполняется:
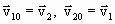 . . | (1.4.58) |
Следовательно, шары при соударении обмениваются скоростями. В частности, если один из шаров одинаковой массы, например второй, до соударения покоится, то после удара он будет двигаться с такой же скоростью, какую имел первоначально первый шар; первый же шар после удара окажется неподвижным.
С помощью формул (1.4.57) можно определить скорость шара после упругого удара о неподвижную или движущуюся стенку. Стенка в этих случаях рассматривается как шар бесконечно большой массы m2 и бесконечно большого радиуса. Разделив числитель и знаменатель соотношений (1.4.57) на m2 и пренебрегая членами, содержащими множитель m1/m2, получим:
 | (1.4.59 ) |
Следовательно, скорость стенки остается постоянной. Скорость же шара, если стенка неподвижна ( ), меняет направление на противоположное. Если стенка движется, величина скорости шара возрастает на 2v0, если стенка движется навстречу шару, и убывает на 2v0, если стенка «уходит» от догоняющего ее шара.
), меняет направление на противоположное. Если стенка движется, величина скорости шара возрастает на 2v0, если стенка движется навстречу шару, и убывает на 2v0, если стенка «уходит» от догоняющего ее шара.
|
|
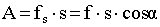
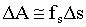

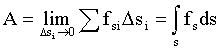

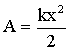

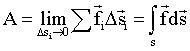
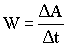
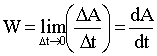
 .Тогда мощность можно представить в виде.
.Тогда мощность можно представить в виде.
