причем
где Линейная скорость
Следовательно, скорость этой точки при сложном движении тела имеет значение:
1.5.2. Движение центра инерции
|
 | (1.5.5) |
где 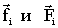 - результирующие всех внутренних и всех внешних сил, действующих на данную элементарную массу. Суммируя, для всех элементарных масс имеем:
- результирующие всех внутренних и всех внешних сил, действующих на данную элементарную массу. Суммируя, для всех элементарных масс имеем:
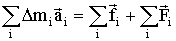 | (1.5.6) |
Однако сумма всех внутренних сил, действующих в системе, равна нулю. Поэтому (1.5.5) можно упростить так:
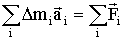 | (1.5.7) |
Используя определение центра инерции, можно записать:
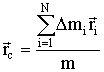 | (1.5.8) |
Дифференцируя (1.5.7) дважды по времени, можно получить:
 | (1.5.9) |
Подставляя (1.5.8) в (1.5.6), имеем:
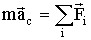 | (1.5.10) |
Следовательно, центр инерции твердого тела движется так, как двигалась бы МТ с массой, равной массе тела, под действием всех приложенных к телу сил.
1.5.3. Момент силы
Рассмотрим схему установки на Рис. 1.5.1.
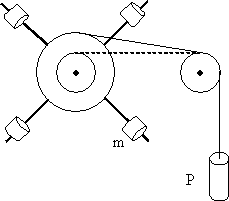
Рис. 1.5.1. Схема установки для исследования
равно-ускоренного вращательного движения
Под действием груза Р крестовина будет вращаться с возрастающей угловой скоростью, и вращение будет равно-ускоренным. Варьируя величину груза Р, радиус шкива l, массу грузов m и их расстояние R от оси вращения, можно прийти к заключению, что угловое ускорение β:
- прямо пропорционально натяжению нити f и радиусу шкива l;
- обратно пропорционально массе грузов m и квадрату их расстояния R от оси вращения.
Следовательно, ускорение вращательного движения зависит не только от величины действующей на тело силы, но и от расстояния l от оси вращения до линии, вдоль которой действует сила. Произведение fl дает величину так называемого момента силы относительно оси вращения.
Из этого опыта следует также, что на величину углового ускорения влияет не только масса вращающегося тела, но и распределение массы относительно оси вращения. Величина, которая это учитывает, называется моментом инерции тела относительно оси вращения.
Моментом силы  относительно некоторой точки О называется величина
относительно некоторой точки О называется величина 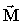 , равная векторному произведению:
, равная векторному произведению:
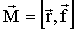 | (1.5.11) |
где 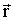 - радиус-вектор, проведенный из точки О в точку приложения силы (Рис. 1.5.2).
- радиус-вектор, проведенный из точки О в точку приложения силы (Рис. 1.5.2).
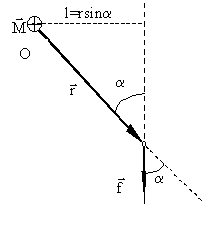
Рис. 1.5.2. К определению момента силы
Вектор 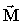 , по определению, перпендикулярен плоскости векторов
, по определению, перпендикулярен плоскости векторов 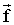 и
и 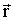 и направлен от нас. Это - аксиальный вектор. Модуль вектора
и направлен от нас. Это - аксиальный вектор. Модуль вектора 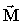 равен:
равен:
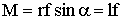 | (1.5.12) |
где α - угол между направлениями векторов 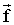 и
и 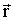 , а l = r sinα - длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила. Эта длина называется плечом силы относительно точки О.
, а l = r sinα - длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила. Эта длина называется плечом силы относительно точки О.
Если можно представить силу в виде суммы сил, имеющих общую точку приложения  , то формулу (1.5.10) можно записать так:
, то формулу (1.5.10) можно записать так:
 | (1.5.13) |
Парой сил называются две равные по величине и противоположно направленные силы, не действующие вдоль одной и той же прямой (Рис. 1.5.3). Расстояние l между прямыми, вдоль которых действуют силы, называется плечом пары сил.

Рис. 1.5.3. Момент пары сил
Покажем, что момент пары сил относительно любой точки будет один и тот же. Пусть точка лежит в плоскости, в которой действуют силы, и выполняется 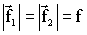 . Момент силы
. Момент силы  равен fl1 и направлен к наблюдателю, момент силы
равен fl1 и направлен к наблюдателю, момент силы  равен fl2 и направлен от наблюдателя. Результирующий момент силы направлен от наблюдателя и равен:
равен fl2 и направлен от наблюдателя. Результирующий момент силы направлен от наблюдателя и равен:
 | (1.5.14) |
Полученное выражение не зависит от положения точки О на плоскости, в которой лежит пара сил.
Суммарный момент внутренних сил Силы, с которыми взаимодействуют друг с другом две любые элементарные массы, лежат на одной и той же прямой (Рис. 1.5.4).
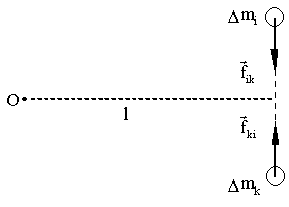
Рис. 1.5.4. Момент внутренних сил
Их моменты относительно произвольной точки О равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы МТ, в частности, для твердого тела, всегда равна нулю.
1.5.4. Момент импульса материальной точки.
Закон сохранения момента импульса
Аналогично моменту силы введем момент импульса МТ относительно некоторой точки О:
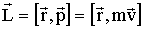 | (1.5.15) |
где  - радиус-вектор, проведенный из точки О в точку пространства, в которой находится МТ (Рис. 1.5.5).
- радиус-вектор, проведенный из точки О в точку пространства, в которой находится МТ (Рис. 1.5.5).
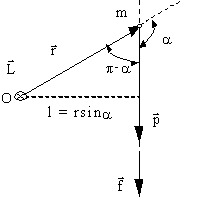
Рис. 1.5.5. К определению момента импульса
Введя плечо l = rsinα, можно получить модуль вектора момента импульса в виде:
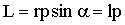 | (1.5.16) |
Продифференцируем (1.5.16) по времени:
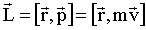 | (1.5.17) |
Первое слагаемое равно нулю в силу того, что оно представляет собой векторное произведение векторов одинакового направления:  . Вектор
. Вектор 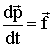 . Поэтому соотношение (1.5.17) можно переписать так:
. Поэтому соотношение (1.5.17) можно переписать так:
 | (1.5.18) |
где 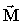 - момент приложенных к МТ сил, взятый относительно той же точки О, относительно которой рассчитан момент импульса
- момент приложенных к МТ сил, взятый относительно той же точки О, относительно которой рассчитан момент импульса  . Для замкнутой системы из N материальных точек легко получить аналогичное (1.5.18) соотношение. В отсутствие или при взаимной компенсации внешних сил их суммарный момент
. Для замкнутой системы из N материальных точек легко получить аналогичное (1.5.18) соотношение. В отсутствие или при взаимной компенсации внешних сил их суммарный момент
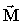 , действующий на тела системы, равен нулю. В результате этого суммарный момент импульса не зависит от времени. Таким образом, формулируется закон сохранения момента импульса: момент импульса замкнутой системы материальных точек остается постоянным.
, действующий на тела системы, равен нулю. В результате этого суммарный момент импульса не зависит от времени. Таким образом, формулируется закон сохранения момента импульса: момент импульса замкнутой системы материальных точек остается постоянным.
1.5.5. Уравнение динамики
вращательного движения
Если МТ вращается по окружности радиуса r (Рис.1.5.6), то момент ее импульса относительно оси вращения О равен:
 | (1.5.19) |
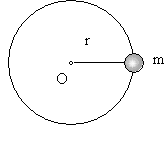
Рис. 1.5.6. К выводу уравнения динамики вращательного двмжения
Пусть ω - угловая скорость вращения, тогда v = ωr, и (1.5.18) будет иметь вид:
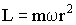 | (1.5.20) |
Если вокруг оси О вращается система МТ с одной и той же угловой скоростью ω, то:
 | (1.5.21) |
где, 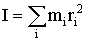 момент инерции системы МТ относительно оси вращения, равный сумме произведений масс МТ на квадраты их расстояний до оси вращения.
момент инерции системы МТ относительно оси вращения, равный сумме произведений масс МТ на квадраты их расстояний до оси вращения.
Если угловая скорость и момент инерции - переменные величины, то, подставляя (1.5.21) в (1.5.18), получим:
 | (1.5.22) |
где М - момент внешних сил относительно оси вращения. Соотношение (1.5.22) - это основное уравнение динамики вращательного движения вокруг неподвижной оси.
Важным частным случаем является вращение неизменяемой системы МТ или твердого тела вокруг неподвижной оси. В этом случае момент инерции I остается постоянным при вращении, и уравнение (1.5.22) будет иметь вид:
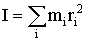 | (1.5.23) |
Сопоставляя уравнения динамики вращательного движения с уравнениями динамики поступательного движения, легко заметить, что при вращательном движении роль силы исполняет момент силы, роль массы - момент инерции и т д. (Табл. 1.5.1).
Таблица 1.5.1
.gif) | .gif) |
.gif) | .gif) |
.gif) | .gif) |
 - сила - сила | 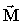 - момент силы - момент силы |
.gif) - масса - масса | .gif) - момент инерции - момент инерции |
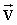 - линейная скорость - линейная скорость |  - угловая скорость - угловая скорость |
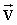 - линейная скорость - линейная скорость |  - угловая скорость - угловая скорость |
.gif) - линейное ускорение - линейное ускорение | 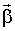 - угловое ускорение - угловое ускорение |
.gif) - импульс - импульс |  - момент импульса - момент импульса |
Предположим, что твердое тело может изменять свою конфигурацию в результате перераспределения масс. Пусть в результате происходит изменение момента инерции от значения I1 до I2. Если такое перераспределение осуществляется при отсутствии моментов внешних сил, то согласно закону сохранения момента импульса должно выполняться равенство:
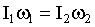 | (1.5.24) |
где ω1 - исходное, а ω2 - конечное значение угловой скорости тела. Следовательно, изменение момента инерции влечет за собой соответственное изменение угловой скорости тела. Этим объясняется такое явление: человек, стоящий на вертящейся скамье, разводя руки в стороны, начинает вращаться медленнее, а, прижимая руки к туловищу, будет вращаться быстрее.
1.5.6. Момент инерции. Теорема Штайнера
Из определения момента инерции:
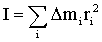 | (1.5.25) |
следует, что момент инерции - величина аддитивная. Это означает, что момент инерции тела равен сумме моментов инерции его частей. Каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции.
Распределение массы в пределах тела можно охарактеризовать с помощью физической величины, называемой плотностью. Если тело однородно, то его плотность может быть вычислена так:
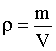 | (1.5.26) |
где m - масса, V - объем тела. Для тела с неравномерно распределенной массой соотношение (1.5.26) дает среднюю плотность. Плотность в данной точке определяется в этом случае так:
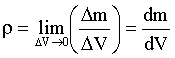 | (1.5.27) |
Уменьшение объема в (1.5.27) следует производить до тех пор, пока не будет получен физически бесконечно малый объем, который достаточно мал, чтобы в его пределах макроскопические свойства вещества можно было считать одинаковыми, и достаточно велик, чтобы не могла проявиться дискретность (атомарное строение) вещества.
Согласно (1.5.27), элементарная масса тела может быть вычислена так:
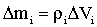 | (1.5.28) |
Следовательно, момент инерции следует записать в виде:
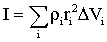 | (1.5.29) |
Если плотность постоянна, ее можно вынести за знак суммы:
 | (1.5.30) |
Устремляя ΔVi к нулю, можно в (1.5.30) перейти к интегрированию:
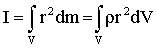 | (1.5.31) |
В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (Рис. 1.5.7).

Рис. 1.5.7. К расчету момента инерции диска
Разобьем диск на кольцевые слои толщиной dr. Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном r. Объем такого слоя равен:
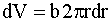 | (1.5.32) |
где b - толщина диска. Поскольку диск однороден, плотность можно вынести за знак интеграла:
 | (1.5.33) |
где R0 - радиус диска. Применяя обозначение для массы диска
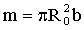 , получим для момента инерции однородного диска:
, получим для момента инерции однородного диска:
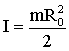 | (1.5.34) |
В данном случае вычисление момента инерции упрощалось благодаря однородности и симметричности тела. Если бы нужно было отыскать момент инерции относительно оси О'О' (Рис. 1.5.7), перпендикулярной к диску и проходящей через его край, вычисления оказались бы значительно сложнее. В таких случаях отыскание момента инерции облегчается, если воспользоваться теоремой Штайнера: момент инерции I относительно произвольной оси равен сумме момента инерции IC относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
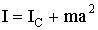 | (1.5.35) |
В соответствии с теоремой Штайнера момент инерции диска относительно оси О'О' равен:
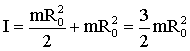 | (1.5.36) |
1.5.7. Работа и кинетическая энергия
вращающегося твердого тела
Если МТ вращается по окружности с радиусом r, то элементарная работа при повороте на угол dφ равна:
 | (1.5.37) |
Такое же выражение получится и для твердого тела, так как его можно рассматривать как систему МТ, вращающихся с общей угловой скоростью ω. Роль силы в (1.5.37) играет момент внешних сил, роль линейного перемещения - угловой поворот.
Кинетическая энергия твердого тела, вращающегося с угловой скоростью ω, может быть записана так:
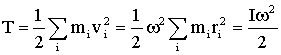 | (1.5.38) |
Это выражение напоминает соответствующую формулу для кинетической энергии МТ и может быть получено из нее формальной заменой m → I, v → ω.
|
|

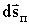 для всех точек тела одно и то же. Разделив
для всех точек тела одно и то же. Разделив 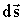 на соответствующий промежуток времени dt, получим скорость точки:
на соответствующий промежуток времени dt, получим скорость точки: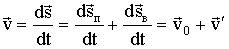
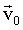 - одинаковая для всех точек тела скорость поступательного движения и
- одинаковая для всех точек тела скорость поступательного движения и 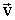 - различная для разных точек тела скорость вращательного движения.
- различная для разных точек тела скорость вращательного движения.
