ТЕМА 1.6. Гидродинамика
Гидродинамика представляет собой раздел механики сплошных сред, в котором изучается движение несжимаемых жидкостей и взаимодействие несжимаемых жидкостей с твердыми телами.
1.6.1. Линии и трубки тока. Неразрывность струи
1.6.2. Уравнение Бернулли
1.6.3. Силы внутреннего трения
Тест 1.6.
1.6.1. Линии и трубки тока. Неразрывность струи
Состояние движения жидкости можно определить, указав для каждой точки пространства вектор скорости как функцию времени. Совокупность векторов 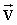 , заданных для всех точек пространства, образует поле векторов скорости. Проведем в движущейся жидкости линии так, чтобы касательная к ним в каждой точке совпадала по направлению с вектором , заданных для всех точек пространства, образует поле векторов скорости. Проведем в движущейся жидкости линии так, чтобы касательная к ним в каждой точке совпадала по направлению с вектором 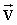 (Рис. 1.6.1). Эти линии называются линиями тока. (Рис. 1.6.1). Эти линии называются линиями тока.
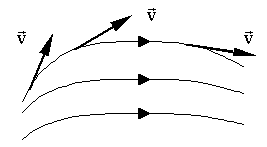
Рис. 1.6.1. Линии тока в жидкости
Густота линий (отношение числа линий к единичной площадке) пропорциональна величине скорости в данном месте.
Картина линий тока может непрерывно меняться. Если вектор скорости в каждой точке пространства остается постоянным, то такое движение называется установившимся, или стационарным. Линии тока в этом случае совпадают с траекториями частиц.
Часть жидкости, ограниченная линиями тока, называется трубкой тока. Вектор скорости будет касательным к поверхности трубки тока; следовательно, частицы жидкости при своем движении не пересекают стенок трубки тока.
Возьмем перпендикулярное к направлению скорости сечение трубки тока S (Рис. 1.6.2).
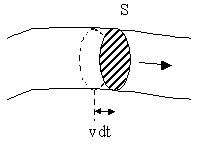
Рис. 1.6.2. Трубка тока
Предположим, что скорость движения частиц жидкости одинакова во всех точках этого сечения. За время dt через сечение S пройдут все частицы, расстояние которых от S в начальный момент времени не превышает значения vdt. Следовательно, за время dt через сечение S пройдет объем жидкости, равный Svdt, а за единицу времени через сечение S пройдет объем жидкости, равный Sv. Возьмем трубку тока, настолько тонкую, что в каждом ее сечении скорость можно считать постоянной. Если жидкость несжимаема (ее плотность одинакова и не изменяется), то количество жидкости между сечениями S1 и S2 (Рис.1.6.3) будет оставаться неизменным.
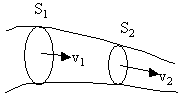
Рис. 1.6.3. К теореме о неразрывности струи
Отсюда следует, что объемы жидкости, протекающие за единицу времени через сечения S1 и S2, должны быть одинаковыми (считаем, что через боковую поверхность трубки тока частицы жидкости не проходят):
Данный результат представляет собой содержание теоремы о неразрывности струи. Из соотношения (1.6.1) следует, что при переменном сечении трубки тока частицы несжимаемой жидкости движутся с ускорением. В горизонтальной трубке тока (Рис.1.6.4) это ускорение может быть обусловлено только непостоянством давления вдоль оси трубки - в местах, где скорость меньше, давление должно быть больше, и наоборот.
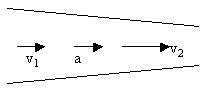
Рис. 1.6.4. Изменение скорости струи
1.6.2. Уравнение Бернулли
Рассматривая движение жидкостей, во многих случаях можно считать, что перемещение одних частей жидкости относительно других не связано с трением. Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной.
Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения (Рис.1.6.5). Рассмотрим малый объем жидкости, ограниченной стенками трубки тока и перпендикулярными сечениями S1 и S2. За время Δt этот объем переместится вдоль трубки тока (сечение S1 переместится в положение S1', пройдя путь Δl1, сечение S2 переместится в положение S2', пройдя путь Δl2). В силу неразрывности струи заштрихованные объемы будут иметь одинаковую величину: ΔV1 = ΔV2 =ΔV.
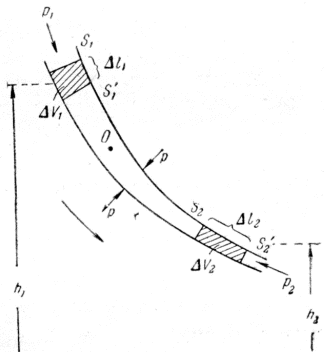
Рис. 1.6.5. К выводу уравнения Бернулли
Энергия каждой частицы жидкости складывается из ее кинетической энергии и потенциальной энергии в поле силы тяжести. Вследствие стационарности течения частица, находящаяся спустя время Δt в любой из точек незаштрихованного объема (например, в точке О), имеет такую же скорость, какую имела частица, находившаяся в той же точке в начальный момент времени. Поэтому приращение энергии ΔЕ можно вычислить как разность энергий заштрихованных объемов ΔV1 и ΔV2.
Возьмем сечение трубки тока и отрезки Δl настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости v, давления р и высоты h. Тогда приращение энергии запишется следующим образом (ρ - плотность жидкости):
В идеальной жидкости силы трения отсутствуют. Поэтому приращение энергии (1.6.2) должно равняться работе, совершаемой над выделенным объемом силами давления. Силы давления на боковую поверхность перпендикулярны в каждой точке к направлению перемещения частиц, к которым оно приложены, и работы не совершают. Отлична от нуля лишь работа сил давления, приложенных к сечениям S1 и S2:
Приравнивая (1.6.2) и (1.6.3), после упрощения получим:
Сечения S1 и S2 были взяты совершенно произвольно. Поэтому полученный результат можно сформулировать следующим образом: в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие:
Данное соотношение носит наименование уравнения Бернулли. Несмотря на то, что оно получено в приближении идеальности жидкости, оно достаточно хорошо выполняется для реальных жидкостей, внутреннее трение в которых не слишком велико.
Пусть жидкость течет так, что скорость имеет во всех точках одинаковую величину. Тогда будет выполняться равенство:
откуда следует, что распределение давления в этом случае будет таким же, как и в покоящейся жидкости.
Для жидкости, текущей горизонтально, выполняется:
т.е. давление оказывается меньшим в тех точках, где скорость больше.
1.6.3. Силы внутреннего трения
Всем реальным жидкостям и газам присуща вязкость, или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается.
Рассмотрим такой опыт. Пусть в жидкость погружены две параллельные друг другу пластины (Рис. 1.6.6), линейные размеры которых значительно превосходят расстояние d между ними.
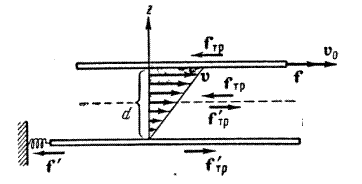
Рис. 1.6.6. Внутреннее трение в жидкостях
Считаем нижнюю пластину неподвижной, а верхняя приводится в движение относительно нижней с некоторой скоростью v0. Опыт показывает, что для перемещения верхней пластины с постоянной скоростью v0 необходимо действовать на нее с вполне определенной постоянной силой 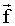 . Поскольку пластина не получает ускорения, то действие этой силы уравновешивается равное по величине, но противоположно направленной силой . Поскольку пластина не получает ускорения, то действие этой силы уравновешивается равное по величине, но противоположно направленной силой  . .
Из опыта следует, что выполняется:
где S - площадь пластин, h - коэффициент пропорциональности, зависящий от природы и состояния жидкости, называемы коэффициентом внутреннего трения или коэффициентом вязкости.
Нижняя пластина при перемещении верхней пластины также оказывается подверженной действию силы 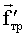 , по величине равной силе , по величине равной силе  . Чтобы нижняя пластина оставалась неподвижной, должно выполняться: . Чтобы нижняя пластина оставалась неподвижной, должно выполняться:  . Воздействие пластин друг на друга осуществляется через жидкость, заключенную между пластинами, передаваясь от одного слоя к другому. Если в любом месте зазора провести плоскость, параллельную пластинам, то можно утверждать, что часть жидкости, лежащая над этой плоскостью, действует на часть жидкости, лежащую под плоскостью, с силой . Воздействие пластин друг на друга осуществляется через жидкость, заключенную между пластинами, передаваясь от одного слоя к другому. Если в любом месте зазора провести плоскость, параллельную пластинам, то можно утверждать, что часть жидкости, лежащая над этой плоскостью, действует на часть жидкости, лежащую под плоскостью, с силой  . Следовательно, соотношение (1.6.8) определяет не только силу трения, действующую на пластины, но и силу трения между соприкасающимися частями жидкости. . Следовательно, соотношение (1.6.8) определяет не только силу трения, действующую на пластины, но и силу трения между соприкасающимися частями жидкости.
Если исследовать скорость частиц жидкости в разных слоях, то оказывается, что она изменяется в направлении z, перпендикулярном к пластинам, по линейному закону:
Действительно, частицы жидкости, непосредственно соприкасающиеся с пластинами, как бы прилипают к ним и движутся с той же скоростью, что и пластины. Из (1.6.9) следует:
Подставляя (1.6.10) в (1.6.8), имеем:
Следовательно, сила трения пропорциональна градиенту скорости.
Единицей вязкости в СИ является такая вязкость, при которой градиент скорости, равный 1 м/с на 1 м, приводит к возникновению силы внутреннего трения в 1 Н на 1 м² поверхности касания слоев (1 Н·с/м²). В СГС единицей вязкости служит 1 пуаз (пз), равный такая вязкость, при которой градиент скорости, равный 1 см/с на 1 см, приводит к возникновению силы внутреннего трения в 1 дин на 1 см² поверхности касания слоев. 1 Н·с/м² = 10 пз.
Коэффициент вязкости зависит от температуры, причем у жидкостей вязкость сильно уменьшается с температурой, у газов, напротив, коэффициент вязкости с температурой возрастает. Такое различие указывает на различие механизма внутреннего трения в жидкостях и газах. При повышении температуры сильно возрастает подвижность молекул в жидкости, что и влечет уменьшение ее вязкости.
|