где N - общее число зарядов. Электрические заряды могут возникать и исчезать. Однако всегда возникают или исчезают одновременно два элементарных заряда противоположных знаков. Поэтому суммарный заряд электрически изолированной системы измениться не может (закон сохранения электрического заряда). Если заряженные частицы, например электроны, могут относительно свободно перемещаться внутри тела, то такое тело способно проводить электрический ток. В качестве носителей заряда могут выступать также положительные или отрицательные ионы. В соответствии со способностью проводить ток все вещества подразделяются на диэлектрики (изоляторы), проводники и полупроводники. При низких температурах многие металлы и некоторые полупроводники начинают проводить электрический ток без потерь. Это - сверхпроводники. Идеальных изоляторов в природе не существует. Все вещества проводят ток хотя бы в ничтожной степени. Однако диэлектрики проводят ток в 1015 - 1020 раз хуже, чем проводники. Полупроводники - это обширная группа веществ, проводящая ток значительно хуже, чем проводники, но лучше, чем диэлектрики. Из опыта установлено, что тела, несущие заряды одинакового знака, отталкиваются, и притягиваются разноименно заряженные тела. Закон взаимодействия точечных зарядов (заряженных тел, размерами которых можно пренебречь по сравнению с расстояниями между телами), был установлен в 1785 г. Ш. Кулоном. Интересно отметить, что несколько ранее этот закон был установлен английским исследователем Г. Кавендишем, но его результаты опубликованы не были. В результате опыта Кулон пришел к выводу, что сила взаимодействия двух точечных зарядов q1 и q2 в вакууме прямо пропорциональна произведению величин этих зарядов и обратно пропорциональна квадрату расстояния между ними:
где k - коэффициент пропорциональности. Для одноименных зарядов сила (3.1.2) положительна, что соответствует отталкиванию. В векторном виде закон Кулона можно записать так:
Коэффициент пропорциональности k зависит от выбора системы единиц. Так, для системы СГСЭ принято, что k = 1. В этой системе, после тщательных измерений, было установлено, что элементарный заряд равен величине Единицей заряда в системе СИ является 1 Кл. Было установлено, что: Вычислим силу, с которой взаимодействовали бы между собой два точечных заряда в 1 Кл, находящиеся в вакууме на расстоянии в 1 м:
Элементарный заряд, выраженный в СИ, равен e = 1,6·10-19 Кл. В системе СИ 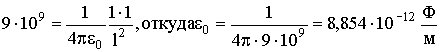 1Ф - это размерность электроемкости. 3.1.2. Электрическое поле.
|
 | (3.1.5) |
Отсюда следует, что сила, действующая на пробный заряд, зависит не только от величин, характеризующих поле (q, 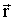 ), но и от величины пробного заряда qпр. Однако легко видеть, что отношение силы к величине пробного заряда будет одно и то же и зависит только от величин (q,
), но и от величины пробного заряда qпр. Однако легко видеть, что отношение силы к величине пробного заряда будет одно и то же и зависит только от величин (q, 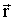 ), определяющих поле в данной точке. Поэтому такое отношение и принимают за величину, характеризующую электрическое поле:
), определяющих поле в данной точке. Поэтому такое отношение и принимают за величину, характеризующую электрическое поле:
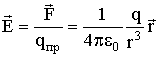 | (3.1.6) |
где вектор  - напряженность электрического поля в данной точке.
- напряженность электрического поля в данной точке.
Направление вектора  совпадает с направлением силы, действующей на положительный заряд. Тогда можно считать, что вектор
совпадает с направлением силы, действующей на положительный заряд. Тогда можно считать, что вектор  направлен от положительного заряда к отрицательному. За единицу напряженности электрического поля принимается напряженность такого поля, в котором на пробный заряд в 1 Кл действует сила в 1Н. Размерность - 1 В/м.
направлен от положительного заряда к отрицательному. За единицу напряженности электрического поля принимается напряженность такого поля, в котором на пробный заряд в 1 Кл действует сила в 1Н. Размерность - 1 В/м.
Перепишем (3.1.6) для произвольной величины заряда:
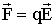 | (3.1.7) |
Уравнение (3.1.7) характеризует силовое действие электрического поля.
Опыт показывает, что сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, которые действуют на данный заряд со стороны каждого из зарядов системы в отдельности. Отсюда вытекает, что напряженность электрического поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый заряд в отдельности:
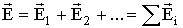 | (3.1.8) |
Данное утверждение носит название принципа суперпозиции (наложения) полей. Принцип суперпозиции позволяет вычислить напряженность поля любой системы зарядов.
Графически напряженность поля можно задать с помощью линий напряженности поля, которые проводятся так, чтобы касательная к ним в любой точке совпадала бы с направлением вектора  . Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности перпендикулярной к линиям площадки, было бы численно равно длине вектора
. Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности перпендикулярной к линиям площадки, было бы численно равно длине вектора  .
.
Линии  точечного заряда представляют собой совокупность радиальных прямых, исходящих или входящих в положительный или отрицательный заряд, соответственно (Рис. 3.1.1).
точечного заряда представляют собой совокупность радиальных прямых, исходящих или входящих в положительный или отрицательный заряд, соответственно (Рис. 3.1.1).
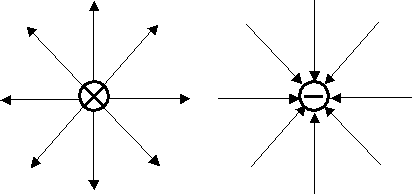
Рис. 3.1.1. Линии напряженности электрического поля точечных зарядов
Линии одним концом опираются на заряд, другим уходят в бесконечность. Отсюда вытекает, что линии  нигде, кроме заряда, не начинаются и не заканчиваются. Это свойство силовых линий является общим для любых электростатических полей.
нигде, кроме заряда, не начинаются и не заканчиваются. Это свойство силовых линий является общим для любых электростатических полей.
Поскольку густота линий  выбирается равной численному значению вектора Е, количество линий, пронизывающих площадку dS, перпендикулярную к вектору
выбирается равной численному значению вектора Е, количество линий, пронизывающих площадку dS, перпендикулярную к вектору  , будет численно равно ЕdS. Если площадка dS ориентирована так, что нормаль к ней образует с вектором
, будет численно равно ЕdS. Если площадка dS ориентирована так, что нормаль к ней образует с вектором  угол α, то количество линий, пронизывающих площадку, будет численно равно:
угол α, то количество линий, пронизывающих площадку, будет численно равно:
 | (3.1.9) |
где Еn - проекция вектора  на направление нормали к площадке dS.
на направление нормали к площадке dS.
Отсюда для произвольной площадки число линий будет равным:
 | (3.1.10) |
Если имеется некоторый вектор 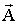 , то выражение
, то выражение
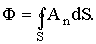 | (3.1.11) |
называется потоком вектора 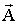 через замкнутую поверхность S. Поэтому из (3.1.11) и (3.1.10) следует, что поток вектора
через замкнутую поверхность S. Поэтому из (3.1.11) и (3.1.10) следует, что поток вектора
 численно равен количеству линий электрического поля, пронизывающих поверхность S.
численно равен количеству линий электрического поля, пронизывающих поверхность S.
3.1.3. Теорема Гаусса
Полное число линий  , пересекающих замкнутую сферическую поверхность произвольного радиуса r, будет равно произведению густоты линий на площадь поверхности сферы 4Πr2. Густота линий равна напряженности электрического поля, поэтому число линий:
, пересекающих замкнутую сферическую поверхность произвольного радиуса r, будет равно произведению густоты линий на площадь поверхности сферы 4Πr2. Густота линий равна напряженности электрического поля, поэтому число линий:
 | (3.1.12) |
Следовательно, поток вектора  через охватывающую заряд сферическую поверхность равен q/ε0. Знак потока совпадает со знаком заряда.
через охватывающую заряд сферическую поверхность равен q/ε0. Знак потока совпадает со знаком заряда.
Для поверхности произвольной формы, если заряд находится внутри нее, поток вектора  также равен q/ε0. Действительно, такая поверхность, как и поверхность сферы, пересекается каждой линией вектора
также равен q/ε0. Действительно, такая поверхность, как и поверхность сферы, пересекается каждой линией вектора  только один раз (Рис. 3.1.2).
только один раз (Рис. 3.1.2).
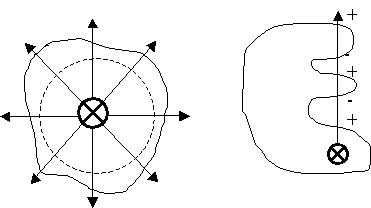
Рис. 3.1.2. К объяснению теоремы Гаусса
Поэтому число пересечений, равное числу линий, выходящих из заряда, также равно q/ε0.
При вычислении потока через складчатую поверхность нужно учесть, что число пересечений данной линией вектора  поверхности может быть только нечетным, причем эти пересечения будут вносить в общий поток попеременно то положительный, то отрицательный вклад. В итоге остается одно "положительное" пересечение этой произвольной поверхности данной линией поля. Таким образом, какова бы ни была форма замкнутой поверхности, охватывающей заряд, поток вектора
поверхности может быть только нечетным, причем эти пересечения будут вносить в общий поток попеременно то положительный, то отрицательный вклад. В итоге остается одно "положительное" пересечение этой произвольной поверхности данной линией поля. Таким образом, какова бы ни была форма замкнутой поверхности, охватывающей заряд, поток вектора  равен q/ε0.
равен q/ε0.
Применяя указанный вывод, а также принцип суперпозиции полей, можно получить в общем виде:
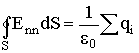 | (3.1.13) |
Данное соотношение носит название теоремы Гаусса. Ее можно сформулировать так: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри зарядов, деленной на ε0.
Если заряды внутри отсутствуют, поток также равен нулю. Если заряды распределены внутри замкнутой поверхности непрерывно с объемной плотностью:
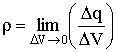 | (3.1.14) |
то соотношение (3.1.13) следует представить в виде:
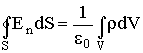 | (3.1.15) |
3.1.4. Работа сил электростатического
поля и его потенциал
Вычислим работу, которая совершается силами поля неподвижного точечного заряда q над перемещающимся в этом поле точечным зарядом q' (Рис. 3.1.3).
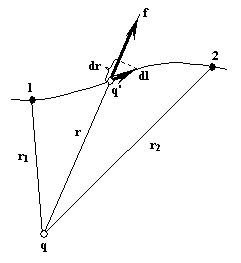
Рис. 3.1.3. Перемещение заряда в электрическом поле
Поскольку dlcosα = dr, то на элементарном пути работа равна:
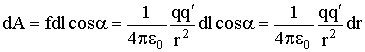 | (3.1.16) |
Отсюда для работы на пути 1-2 получается выражение:
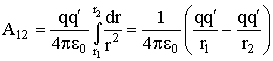 | (3.1.17) |
Полученный результат свидетельствует о том, что работа не зависит от пути перемещения электрического заряда, а зависит от его начального и конечного положений. Следовательно, силы, действующие на заряд q' в поле неподвижного заряда q, являются потенциальными.
Из механики известно, что работа потенциальных сил на замкнутом пути равна нулю. Работа, совершаемая силами поля над зарядом q' при его обходе по замкнутому контуру, может быть представлена так:
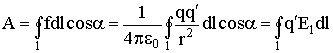 | (3.1.18) |
где E1 - проекция вектора электрического поля на направление элементарного перемещения.
Приравнивая (3.1.18) к нулю и сокращая на постоянный множитель q', приходим к соотношению:
 | (3.1.19) |
которое должно выполняться для любого замкнутого контура.
Выражение вида 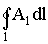 называется циркуляцией вектора
называется циркуляцией вектора 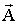 по данному контуру. Таким образом, циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю.
по данному контуру. Таким образом, циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю.
Перемещающийся в поле неподвижного точечного заряда q заряд q' обладает потенциальной энергией, за счет которой и совершается работа против сил электростатического поля. Следовательно, работа (3.1.18) может быть представлена как разность потенциальной энергии в точках 1 и 2:
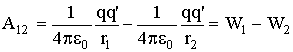 | (3.1.20) |
Отсюда для потенциальной энергии заряда q' в поле неподвижного точечного заряда q получаем общее выражение:
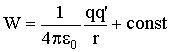 | (3.1.21) |
Значение константы выбирают так, чтобы при удалении заряда на бесконечность потенциальная энергия обращалась в нуль. При этом условии имеем:
 | (3.1.22) |
Как следует из (3.1.22), разные пробные заряды будут иметь разную потенциальную энергию. Однако отношение:
 | (3.1.23) |
оказывается одним и тем же для разных пробных зарядов и может служить энергетической характеристикой данного электростатического поля. Величина φ - потенциал поля в данной точке, который численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.
Если поле создается системой точечных зарядов, то потенциал суммируется:
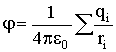 | (3.1.24) |
Следовательно, потенциал электростатического поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Для общего случая можем записать потенциальную энергию заряда q, находящегося в поле с потенциалом φ:
 | (3.1.25) |
Поэтому работа сил электростатического поля над зарядом q может быть выражена через разность потенциалов так:
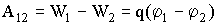 | (3.1.26) |
Если заряд q из точки с потенциалом φ удаляется на бесконечность, то работа сил электростатического поля будет равна:
 | (3.1.27) |
Отсюда следует, что потенциал численно равен работе, которую совершают силы электростатического поля над единичным положительным зарядом при его удалении из данной точки поля на бесконечность. Такую же работу надо совершить против сил электростатического поля для перемещения единичного положительного заряда из бесконечности в данную точку поля.
В СИ за единицу потенциала 1 В принимается потенциал в такой точке, для перемещения в которую из бесконечности заряда в 1 Кл нужно совершить работу в 1 Дж; 1 Дж = 1 В · 1 Кл, поэтому
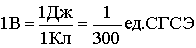 | (3.1.28) |
Часто применяется единица работы в 1 эВ, под которой подразумевается работа, совершаемая силами электростатического поля над зарядом, равным заряду электрона при его прохождении разности потенциалов в 1 В:
1 эВ = 1,60·10-19 Кл·1В = 1,60·10-19 Дж = 1,60·10-12 эрг.
Отметим, что величина kБТ, характеризующая среднюю энергию теплового движения молекул, при комнатной температуре равна:
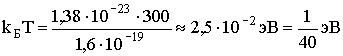
3.1.5. Связь между напряженностью
электростатического поля и его потенциалом
Работа сил поля над зарядом q на отрезке пути dl может быть представлена как qE1dl, с другой стороны - как убыль потенциальной энергии заряда:  .
.
Поэтому можно записать:
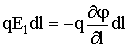
откуда следует, что:
 | (3.1.29) |
где через l обозначено произвольное направление в пространстве.
В частности, для компонент электрического поля можно записать:
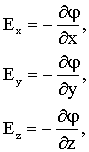 | (3.1.30) |
откуда
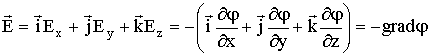 | (3.1.31) |
поскольку стоящее в круглых скобках выражение - это градиент потенциала. Эта функция обладает следующими свойствами: направление градиента потенциала совпадает с направлением  , в котором функция φ при перемещении в пространстве изменяется с наибольшей скоростью.
, в котором функция φ при перемещении в пространстве изменяется с наибольшей скоростью.
Соотношение (3.1.31) позволяет найти напряженность поля в каждой точке, или, напротив, решить обратную задачу - по заданным значениям напряженности поля найти разность потенциалов. Для этого запишем:
 | (3.1.32) |
Для разности потенциалов между двумя бесконечными разноименно заряженными плоскостями получим соотношение из (3.1.32)
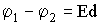 | (3.1.33) |
где d - расстояние между пластинами.
|
|
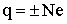
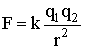
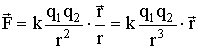
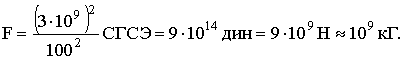
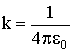 . Чтобы найти численное значение электрической постоянной ε0, используем сделанный расчет (3.1.4). Подставляя это значение силы для тех же зарядов в 1 Кл и расстояние 1 м в (
. Чтобы найти численное значение электрической постоянной ε0, используем сделанный расчет (3.1.4). Подставляя это значение силы для тех же зарядов в 1 Кл и расстояние 1 м в (