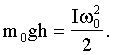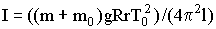Лабораторная работа № 2.
Изучение законов вращательного движения твердого тела
Упражнение №3. Определение момента инерции твердых тел с помощью трифилярного подвеса
Цель работы: изучение основного закона вращения твердого тела и методов определения момента инерции тел различных форм.
Литература:§§ 11-12, 16-18
Приборы и материалы: трифилярный подвес, секундомер, штангенциркуль, масштабная линейка, образцы для измерения.

Для измерения моментов инерции служит трифилярный подвес, устройство которого поясняется на рисунке 3. Подвижная платформа Р' подвешена к платформе Р на трех симметрично расположенных нитях АА', ВВ', СС'. Платформа Р укреплена на кронштейне и снабжена рычагом, при помощи которого системе можно сообщать вращательный момент. Если повернуть нижнюю платформу Р' вокруг вертикальной оси на некоторый угол φ относительно верхней, то возникает момент сил, стремящийся вернуть платформу в положение равновесия. В результате этого платформа начнет совершать крутильные колебания, при этом центр масс платформы будет перемещаться по оси вращения. Период колебания платформы определяется величиной момента инерции платформы; он будет другим, если платформу нагрузить каким-либо телом; этим и пользуются в настоящей работе. Если платформа массы m0, вращаясь в одном направлении, поднялась на высоту h, то приращение потенциальной энергии будет равно Е = m0gh, где g - ускорение силы тяжести. Вращаясь в другом направлении, платформа придет в положение равновесия с кинетической энергией, равной

где I - момент инерции платформы; ω0 - угловая скорость платформы в момент прохождения положения равновесия. Если пренебречь трением, то на основании закона сохранения механической энергии для колеблющейся платформы можно написать следующее равенство:
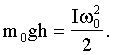 | (1.1) |
Исходя из равенства (1.1) и считая, что платформа при малых углах поворота будет совершать гармонические колебания, можно путем несложных расчетов получить формулу для определения момента инерции платформы:
 | (1.2) |
где l0 - длина нитей подвеса; R,r - расстояния от центров платформы до точек крепления нитей на них; Т0 - период колебания платформы.
Если платформу нагрузить исследуемым телом массой m, то по формуле (1.2) определяется момент инерции платформы вместе с телом. Обозначим его I. Тело на платформе помещается так, чтобы центр масс его находился в центре платформы. Тогда 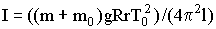
Обозначим момент инерции тела Iт. Величина момента инерции тела
Iт = I - I0. Таким образом, для определения момента инерции платформы ненагруженной или с грузом достаточно измерить R, r, l и с помощью секундомера определить период колебания платформы (T=t/N). Для этого при помощи рычага, находящегося на верхней платформе, нужно сообщить платформе вращательный момент и измерить время(t) некоторого числа (N) полных колебаний (N = 10-15). Опыт по определению периода провести 3 раза и в расчеты взять среднее значение периода Тср. Амплитуда колебаний платформы не должна превышать 8 - 10°. Вращательный момент сообщать платформе при полном покое платформы, чтобы не возникали другие, не крутильные колебания.
Таблица 1
Задание. Определите момент инерции тела неправильной формы
| № | N | t | T0 | T0 ср | m0 | R | r | l | I0 | ΔI0 | (ΔI0/I0)·100% |
|---|
| Ед.изм | | | | | | | | | | | |
| 1 | | | | | | | | | | | |
| 2 | | | | | | |
| 3 | | | | | | |
Таблица 2
Контрольные вопросы
- Что называется моментом силы относительно неподвижной точки? Относительно неподвижной оси? Как определяется направление момента силы?
- Что называется моментом инерции материальной точки? Твердого тела?
- Дайте определения угловой скорости, угловому ускорению.
- Запишите основной закон динамики вращательного движения ?
- Сопоставьте основные уравнения динамики поступательного и вращательного движения, прокомментируйте их аналогию.
- Как определяется кинетическая энергия вращающегося тела?
- Сформулировать и записать теорему Штейнера?
- Что такое трифилярный подвес?
- Как определить момент инерции тел с помощью трифилярного подвеса?
- От чего зависит период колебания платформы?
|