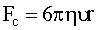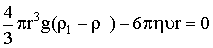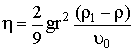Лабораторный практикум

Лабораторная работа №3.
Определение коэффициента внутреннего трения жидкостей

Цель работы: изучение течения вязкой жидкости и методов определения коэффициента внутреннего трения жидкости.

Литература: §§ 31-33, 48.

Приборы и материалы:стеклянный цилиндр с исследуемой жидкостью, мелкие шарики, штангенциркуль, секундомер, масштабная линейка.

На всякое тело, движущееся в вязкой жидкости, действует сила сопротивления. Стоксом было показано, что при ламинарном обтекании шарика безграничной жидкостью сила сопротивления определяется формулой

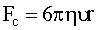(1.1)

где η - коэффициент внутреннего трения жидкости; ν - скорость шарика; r - радиус шарика. Характер обтекания определяется значением числа Рейнольдса:

(1.2)

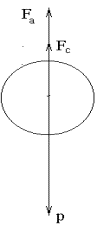
где ρ - плотность жидкости; r - радиус шарика; v - cкорость шарика; η - коэффициент внутреннего трения жидкости. Обтекание является ламинарным при небольших значениях Re (малая скорость движения и радиус шарика). Рассмотрим свободное падение шарика в вязкой жидкости. На шарик действуют три силы: сила тяжести (Р), архимедова сила (F_a), cила сопротивления (F_c), зависящая от скорости. Запишем уравнение движения шарика в жидкости в соответствии со 2-м законом Ньютона:

(1.3)

где ρ₁ - плотность вещества шарика; ρ - плотность жидкости; g - ускорение силы тяжести. Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается и, наконец, шарик достигает такой скорости, при которой ускорение становится равным нулю. Тогда уравнение (1.3) принимает вид:

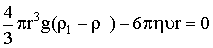(1.4)

В этом случае шарик движется с постоянной скоростью v₀. Такое движение шарика называется установившимся. Решая уравнение (1.4) относительно коэффициента внутреннего трения, получаем

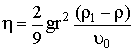(1.5)

Зная величины, входящие в правую часть равенства, можно определить коэффициент внутреннего трения жидкости.

Установка для измерения коэффициента внутреннего трения представляет собой стеклянный цилиндр, наполненный исследуемой жидкостью. Цилиндр укреплен на подставке, которая устанавливается строго вертикально. Для измерения коэффициента внутреннего трения жидкости употребляются очень мелкие шарики из свинца. Диаметр этих шариков измеряем штангенциркулем. Измерив, радиус шарика r, опускаем его в цилиндр с жидкостью, как можно ближе к оси цилиндра (предварительно необходимо выбрать на цилиндре метки, между которыми будет измеряться время движения шарика: первая – на расстоянии 10 см от поверхности жидкости; вторая - на расстоянии 15 см от первой). В момент прохождения шарика через 1-ю метку пускаем в ход секундомер, в момент прохождения шарика через 2–ю метку останавливаем секундомер.

Измерив, расстояние l между метками и, считая, что к моменту прохождения шариком метки 1 скорость его уже установилась, получаем v₀= l/t, где t - время прохождения шариком расстояния между метками. Таким образом, зная v₀, r, ρ₁, ρ, по формуле (1.5) рассчитайте коэффициент внутреннего трения жидкости. Опыт проведите для пяти разных шариков и для каждого шарика рассчитайте η, затем определите среднее значение η_ср, среднюю квадратичную ошибку (Δη) и относительную ошибку (ε =(Δη/η_ср)·100%). По формуле (1.2) рассчитайте число Рейнольдса и сделайте вывод о характере обтекания шарика жидкостью. Результаты измерений представьте в таблице.

Таблица 1

Контрольные вопросы

1. От чего зависит сила внутреннего трения, как она направлена?
2. Что называется коэффициентом внутреннего трения, единицы измерения?
3. Сформулируйте и запишите закон Стокса.
4. Какие силы действуют на шарик, падающий в жидкости?
5. Почему, начиная с некоторого момента времени, шарик движется равномерно?
6. Как изменяется скорость движения шарика с увеличением его радиуса?