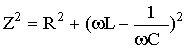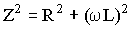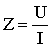Лабораторная работа № 14.
Измерение полного сопротивления
и индуктивности соленоида
Цель работы: освоить методы определения полного сопротивления обмотки соленоида и его индуктивности.
Литература: §§ 120, 122, 126, 149.
Приборы и материалы: соленоид, ферромагнитный сердечник, лабораторный автотрансформатор (ЛАТР), миллиамперметр, вольтметр, нагрузочное сопротивление (реостат).
Обычно соленоидом называют свернутый в спираль изолированный проводник, по которому течет электрический ток. Он обладает значительной индуктивностью, сравнительно малым активным сопротивлением, небольшой емкостью и может быть элементом электрической цепи. В цепи переменного тока полное сопротивление соленоида будет равно:
 | (1.1) |
где R - активное сопротивление проводника соленоида; X - реактивное, равное разности индуктивного сопротивления XL = ωL и емкостного сопротивления Xc=1/(ωC). Ток, текущий в соленоиде, создает в окружающем пространстве магнитное поле, причем магнитный поток Ф, пронизывающий соленоид, прямо пропорционален току I: Ф = LI. Коэффициент пропорциональности L называют коэффициентом самоиндукции или индуктивностью. Индуктивность L зависит от размеров, формы и числа витков соленоида, а также от магнитной проницаемости среды (от магнитных свойств сердечника) и в системе СИ измеряется в генри ( Гн ). Формулу для полного сопротивления соленоида можно переписать в виде:
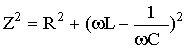 | (1.2) |

Для соленоида с небольшим числом витков емкостным сопротивлением можно пренебречь. Тогда получим:
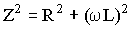 | (1.3) |
Рис.1. Схема установки для определения индуктивности соленоида: АТ - автотрансформатор (ЛАТР); ТР - понижающий трансформатор; К - ключ; R - нагрузочное сопротивление; mA - миллиамперметр; L - соленоид; V - вольтметр.
Задание 1. Определить полное сопротивление Z соленоида.
Соберите схему в соответствии с рис. 1. Полное сопротивление соленоида можно определить по закону Ома, если измерить значение силы переменного тока в обмотке соленоида при соответствующих значениях напряжения на концах обмотки (на клеммах соленоида):
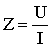 | (1.4) |
Измерения U и I произведите 5 раз, постепенно увеличивая значения напряжения в цепи. Данные измерений занести в табл. 1:
Таблица 1
| Без сердечника | С сердечником |
| № | U | I | Z | U | I | Z |
| Ед.изм. | | | | | |
| 1. | | | | | | |
Задание 2. Определить индуктивность соленоида L.
Из формулы (1.3) вытекает:
 | (1.5) |
Активное сопротивление исследуемого соленоида известно и равно R = 24 Ом. Циклическая частота ω=2πv, где v=50 Гц (сетевая частота).
Таблица 2
| Без сердечника | С сердечником |
| № | Z | L | Lср | ΔLср | Z | L | Lср | ΔLср |
| Ед.изм. | | | | | | | |
| 1. | | | | | | | | |
Для каждого измеренного в задании 1 полного сопротивления Z по формуле (1.5) вычислите индуктивность соленоида без сердечника и индуктивность соленоида с сердечником. Данные расчетов занесите в табл. 2.
Контрольные вопросы
- Что такое магнитный поток? Единицы измерения магнитного потока.
- Что такое индуктивность? Единицы измерения индуктивности.
- От чего зависит величина индуктивности соленоида?
- Запишите закон Ома для цепи переменного тока с активным сопротивлением, индуктивностью и емкостью.
- Как можно определить индуктивность соленоида, если известны его полное и активное сопротивления?
|