ТЕМА 3.9. ПЕРЕМЕННЫЙ ТОК
3.9.1 Квазистационарные токи
3.9.2. Переменный ток, текущий через индуктивность
3.9.3. Переменный ток, текущий через емкость
3.9.4. Переменный ток, текущий через цепь с емкостью, индуктивностью и активным сопротивлением
3.9.5. Мощность, выделяемая в цепи переменного тока
3.9.6. Свободные колебания тока в электромагнитном контуре без потерь
3.9.7 Электромагнитные волны
3.9.1 Квазистационарные токи
Закон Ома и вытекающие из него правила Кирхгофа были установлены для постоянных токов. Однако эти законы остаются справедливыми и для мгновенных значений изменяющихся во времени тока или напряжения, если их изменения происходят не слишком быстро. Электромагнитные возмущения распространяются по цепи со скоростью света с. Если за время τ = l/c, которое необходимо для передачи возмущения в самую отдаленную точку цепи l, сила тока изменяется незначительно, то мгновенные значения тока в начале и конце цепи будут практически одинаковыми. Токи, удовлетворяющие такому условию, называются квазистационарными. Для них справедливо неравенство:
где Т – период изменения тока.
При размерах цепи l ~ 3 м τ = 10-8 с. Таким образом, вплоть до периодов Т ~ 10-6 с, что соответствует частоте 106 Гц, токи в такой цепи можно считать квазистационарными. Ток промышленной частоты 50 Гц будет квазистационарным для цепей длиной l ~ 100 км.
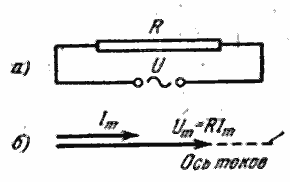
Рис.3.9.1. Представление переменных токов с помощью векторных диаграмм
Мгновенные значения квазистационарного тока подчиняются закону Ома, и для него справедливы правила Кирхгофа. Пусть к зажимам сопротивления R (Рис.3.9.1), не обладающего индуктивностью или емкостью (такое сопротивление называется активным), приложено напряжение, изменяющееся со временем по закону:
где Um – амплитудное значение напряжения. При выполнении условия квазистационарности ток через сопротивление определяется законом Ома:
Здесь введено обозначение амплитудного значения тока:
Удобно при описании переменных токов использовать векторные диаграммы. Выберем произвольное направление, которое назовем осью токов. Отложим вдоль этого направления вектор тока длиной Im. Поскольку напряжение и ток в данном случае изменяются во времени синхронно, вектор напряжения также будет направлен вдоль оси токов. Его длина равна RIm.
3.9.2. Переменный ток, текущий через индуктивность

Рис.3.9.2. Переменный ток, текущий через индуктивность
Подадим переменное напряжение на концы индуктивности L с пренебрежимо малыми сопротивлением и емкостью (Рис.3.9.2). Через индуктивность будет течь переменный ток, вследствие чего возникнет ЭДС самоиндукции:
Используя второе правило Кирхгофа, можем записать:
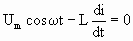 , ,
следовательно,
В данном случае все напряжение приложено к индуктивности. Следовательно, величина
и есть падение переменного напряжения на индуктивности.
Перепишем уравнение (3.9.6) в виде:
Интегрируя (3.9.8), получим:
Постоянный ток в данном примере отсутствует, поэтому const = 0. Следовательно, имеем:
где
Из сопоставления (3.9.11) и (3.9.4) следует, что роль сопротивления в цепи с индуктивностью играет величина:
которую называют реактивным индуктивным сопротивлением.
Как видно из (3.9.12), величина индуктивного сопротивления растет при увеличении частоты тока. Постоянному току индуктивность сопротивления не оказывает.
Используя (3.9.6) и (3.9.11), падению напряжения на индуктивности можно придать вид:
Из сравнения (3.9.13) и (3.9.10) следует, что между током и напряжением в цепи с индуктивностью существует сдвиг фаз на 900, причем ток отстает по фазе от напряжения. На векторной диаграмме это обстоятельство можно отразить как на Рис.3.9.2б.
3.9.3. Переменный ток, текущий через емкость
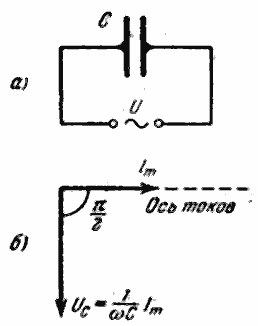
Рис.3.9.3. Ток и напряжение в цепи с емкостью
Пусть переменное напряжение подано на емкость С (Рис.3.9.3) Индуктивностью и сопротивлением подводящих проводов пренебрегаем. Емкость непрерывно перезаряжается, благодаря чему через нее протекает переменный ток. Напряжение на конденсаторе можно считать равным внешнему напряжению:
Умножая (3.9.14) на С и дифференцируя по времени, получим ток:
где
Величина ХС в цепи с емкостью играет роль сопротивления и называется реактивным емкостным сопротивлением.
Для постоянного тока ХС = ±, так как постоянный ток течь через конденсатор не может. Переменный ток через конденсатор проходит, причем сопротивление току тем меньше, чем больше частота.
Заменив в соотношении (3.9.14) амплитуду напряжения, используя (3.9.16), имеем:
Сравнив (3.9.17) и (3.9.15), можно сделать вывод, что между током и напряжением в цепи с емкостью существует сдвиг фаз на 900, причем ток опережает по фазе напряжение. На векторной диаграмме это обстоятельство можно отразить как на Рис. 3.9.3б.
3.9.4. Переменный ток, текущий через цепь с емкостью, индуктивностью и активным сопротивлением
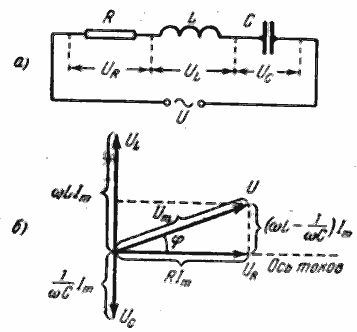
Рис.3.9. 4. Цепь с индуктивностью, емкостью и активным сопротивлением
Рассмотрим цепь, включающую в себя активное сопротивление, индуктивность и емкость (Рис.3.9.4). Подадим на эту цепь переменное напряжение с частотой ω
. В цепи возникнет переменный ток с той же частотой. Он вызовет падение напряжения на активном сопротивлении UR. Фаза этого напряжения совпадает с фазой тока, поэтому вектор напряжения откладывают вдоль оси токов. Падение напряжения на индуктивности UL опережает ток по фазе на 900, поэтому вектор, изображающий UL, должен быть повернут относительно оси токов на 900 против часовой стрелки. Наконец, падение напряжения на емкости UС отстает по фазе от тока на 900 и должно быть изображено вектором UС, повернутым относительно оси токов на 900 по часовой стрелки.
Сложив векторы, изображающие UL, UR и UС, получим вектор, изображающий приложенное напряжение U. Его длина равна Um. Этот вектор образует с осью токов угол φ, тангенс которого можно вычислить из Рис.3.9.4:
Угол φ дает разность фаз между напряжением U и силой тока i. Из Рис.3.9.4 следует также, что:
откуда имеем:
Итак, если напряжение на зажимах цепи изменяется по закону:
то в такой цепи будет течь ток:
Величина
называется полным сопротивлением цепи. При этом величина
носит наименование реактивного сопротивления. Поэтому формулу (3.9.23) можно представить в виде:
Ток отстает от напряжения (φ > 0) или опережает его (φ
< 0) в зависимости от соотношения между ХL и ХС.
- Если
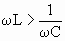 , то φ > 0, и ток отстает от напряжения по фазе; , то φ > 0, и ток отстает от напряжения по фазе;
- Если
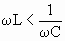 , то φ < 0, и ток опережает напряжение по фазе; , то φ < 0, и ток опережает напряжение по фазе;
- Если

, то φ = 0, и ток и напряжение изменяются синфазно.
Для выполнения 3 условия необходимо, чтобы частота имела значение:
Если частота внешнего напряжения имеет значение (3.9.25), полное сопротивление цепи имеет наименьшее значение, равное:
Соответственно, сила тока будет иметь наибольшее значение. При этом падение напряжения на активном сопротивлении равно внешнему напряжению, приложенному к цепи:
Падения напряжения на индуктивности и емкости равны по амплитуде и противоположны по фазе. Это явление называется резонансом напряжений, а частота (3.9.25) – резонансной.
При ω = ωрез имеем для амплитуд напряжений на индуктивности  и емкости и емкости  : :
Если  , то падения напряжения на индуктивности и емкости будут превышать напряжение, приложенное к цепи. , то падения напряжения на индуктивности и емкости будут превышать напряжение, приложенное к цепи.
Если емкость в цепи отсутствует, приложенное напряжение равно сумме напряжений на сопротивлении и индуктивности (Рис. 3.9.5):
Тогда из Рис. 3.9.5 следует, что:
Эти формулы совпадут с выражениями (3.9.18) и (3.9.20) соответственно, если в последних положить  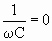 , т.е. С = ±
. Таким образом, отсутствие емкости в цепи означает именно условие С = ±
. Действительно, постепенный переход от цепи, содержащей емкость, к цепи без емкости можно представить себе как сближение обкладок конденсатора вплоть до их полного соприкосновения. Но в этом случае расстояние между ними уменьшается, а емкость возрастает. , т.е. С = ±
. Таким образом, отсутствие емкости в цепи означает именно условие С = ±
. Действительно, постепенный переход от цепи, содержащей емкость, к цепи без емкости можно представить себе как сближение обкладок конденсатора вплоть до их полного соприкосновения. Но в этом случае расстояние между ними уменьшается, а емкость возрастает.
3.9.5. Мощность, выделяемая в цепи переменного тока
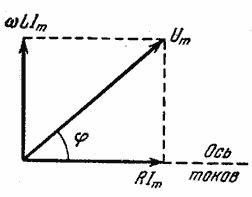
Рис.3.9.5. Векторная диаграмма для цепи с индуктивностью и сопротивлением
Мгновенное значение мощности, выделяемой в цепи, равно произведению мгновенных значений напряжения и силы тока:
Пользуясь формулой:
 , ,
соотношению (3.9.31) можно придать вид:
Практический интерес представляет среднее по времени значение Р(t), которое обозначим через Р. Так как среднее значение cos(2ωt-φ
) = 0, то выполняется:
Средняя мощность выделяется в активном сопротивлении в виде тепла. Используя векторную диаграмму Рис. 3.9.4, можно получить:
Подставляя (3.9.34) в (3.9.33) и учитывая, что 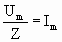 , получаем: , получаем:
Такую же мощность развивает постоянный ток, для которого сила тока равна величине:
Величина (3.9.36) называется действующим, или эффективным, значением силы тока. Аналогично для напряжения имеем действующее значение:
Используя (3.9.36) и (3.9.37), формулу (3.9.33) можно представить в виде:
Входящий в (3.9.38) множитель cosφ называют коэффициентом мощности. Если реактивное сопротивление Х = 0, то, согласно (3.9.34), cosφ = 1, и P = UI (выделяется максимальная мощность). При чисто реактивном сопротивлении цепи R = 0 и cosφ = 0, поэтому средняя мощность также равна нулю. В данном случае невозможно получить выделяемую мощность, отличную от нуля. В электротехнике для сокращения потерь поэтому стремятся сделать значение cosφ как можно больше.
3.9.6. Свободные колебания тока в электромагнитном контуре без потерь
В цепи, содержащей параллельно соединенные индуктивность и емкость, возникают электрические колебания. Такая цепь называется колебательным контуром (Рис.3.9.6).

Рис.3.9.6. Электромагнитные колебания в колебательном контуре
Для того, чтобы вызвать колебания, можно присоединить отключенный от индуктивности конденсатор к источнику тока, вследствие чего на обкладках возникнут разноименные заряды величиной qm (стадия 1). Между обкладками возникнет электрическое поле, энергия которого равна 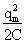 . Если затем отключить источник тока и замкнуть конденсатор на индуктивность, емкость начнет разряжаться, и в контуре потечет ток. В результате энергия электрического поля начнет уменьшаться, но зато возникнет все возрастающая энергия магнитного поля, обусловленная током, текущим через индуктивность. Эта энергия равна величине . Если затем отключить источник тока и замкнуть конденсатор на индуктивность, емкость начнет разряжаться, и в контуре потечет ток. В результате энергия электрического поля начнет уменьшаться, но зато возникнет все возрастающая энергия магнитного поля, обусловленная током, текущим через индуктивность. Эта энергия равна величине 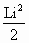 . .
Так как считается, что активное сопротивление равно нулю, полная энергия 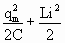 не расходуется на нагревание и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе и энергия электрического поля в нем равны нулю, энергия магнитного поля и величина тока достигают максимального значения (стадия 2). не расходуется на нагревание и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе и энергия электрического поля в нем равны нулю, энергия магнитного поля и величина тока достигают максимального значения (стадия 2).
В дальнейшем ток уменьшается и, когда заряды на обкладках конденсатора достигнут первоначальной величины, сила тока становится равной нулю (стадия 3). Отметим, что знаки зарядов на обкладках конденсатора противоположны тем, что были на начальном уровне.
Затем те же процессы протекают в обратном порядке (стадии 4 и 5), и весь цикл повторяется снова и снова. В ходе описанного процесса периодически изменяются (колеблются) заряд на обкладках, напряжение на конденсаторе, сила тока, текущего через индуктивность.
Колебаниям в контуре можно сопоставить колебания пружинного маятника.
Из сопоставления электрических и механических колебаний следует, что энергия электрического поля 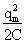 аналогична потенциальной энергии упругой деформации, а энергия магнитного поля аналогична потенциальной энергии упругой деформации, а энергия магнитного поля 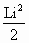 аналогична кинетической энергии. Индуктивность L играет роль массы m, величина, обратная емкости С-1, - роль коэффициента жесткости k. Наконец, заряду q соответствует смещение маятника х, а силе тока аналогична кинетической энергии. Индуктивность L играет роль массы m, величина, обратная емкости С-1, - роль коэффициента жесткости k. Наконец, заряду q соответствует смещение маятника х, а силе тока 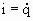 - скорость. - скорость.
Во время колебаний внешнее напряжение к контуру не приложено. Поэтому падения напряжения на емкости и на индуктивности в сумме должны дать нуль:
Разделив (3.9.39) на величину L и используя выражение для тока 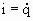 , получим: , получим:
Если ввести обозначение:
то уравнение (3.9.40) принимает вид:
Это дифференциальное уравнение 2 порядка, известное как уравнение колебаний. Его решением является функция:
Следовательно, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой, определяемой формулой (10.41). Это – собственная частота контура. Для периода колебаний из (10.41) можно получить формулу Томсона:
3.9.7 Электромагнитные волны
В процессах преобразования электрической энергии в энергию магнитного поля и обратно, происходящих в электромагнитном контуре, возникают электромагнитные колебания, обусловленные неразрывной связью между переменным магнитным и переменным электрическим полями. Максвелл теоретически вычислил, что такие электромагнитные колебания могут распространяться в свободном пространстве со скоростью света, приобретая при этом свойства электромагнитных волн (Рис.3.9.7).
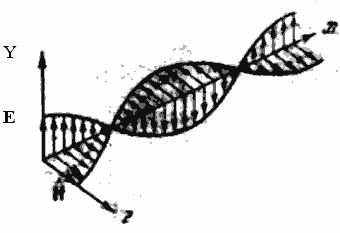
Рис.3.9.7. Структура электромагнитной волны
Как видно из рисунка, векторы электрического и магнитного полей образуют с направлением распространения правовинтовую систему. В фиксированной точке пространства эти векторы изменяются со временем по гармоническому закону. Поскольку волна должна распространяться в пространстве, векторы электрического и магнитного полей должны зависеть от координаты:
Это – уравнения плоской электромагнитной волны, где
модуль волнового вектора, совпадающего с направлением распространения электромагнитной волны, ω и λ - циклическая частота и длина волны,
скорость электромагнитной волны, совпадающая со скоростью света.
Экспериментальное подтверждение теории Максвелла было сделано Г.Герцем в 1888г. Для получения волн Герц использовал изобретенный им вибратор. В колебательном контуре электрическое поле сосредоточено между обкладками конденсатора, а магнитное – внутри катушки. В окружающее пространство эти поля попасть не могут. Чтобы появилось излучение, нужно модифицировать колебательный контур, сделать его открытым. Этого можно достигнуть, увеличивая расстояние между пластинами конденсатора и между витками катушки (Рис.3.9.8). В пределе можно прийти к вибратору Герца – устройству, которое будет излучать электромагнитные волны, если через вибратор пропускать переменный электрический ток.

Рис.3.9.8. Открытый колебательный контур
|