РАЗДЕЛ VII. ВВЕДЕНИЕ В КВАНТОВУЮ МЕХАНИКУ
Основные законы и формулы
Примеры решения задач
Задачи для самостоятельного решения
Качественные задачи
Контрольные вопросы
При решении задач этого раздела не следует забывать, что при скоростях, сравнимых со скоростью света, необходимо использовать релятивистские соотношения, а в задачах на применение соотношений неопределенностей Гейзенберга - эти соотношения позволяют качественно описать многие закономерности движения микрочастиц.
Основные законы и формулы
| Длина волны де Бройля | 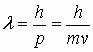 |
| Одномерное уравнение Шредингера для стационарных состояний | 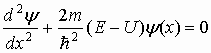 |
| Плотность вероятности | 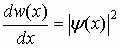 |
| Вероятность обнаружения частицы в интервале от х1 до х2 | 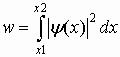 |
| Соотношения неопределенности Гейзенберга для координаты и импульса, энергии и времени |  |
| Импульс релятивистской частицы и его связь с кинетической энергией | 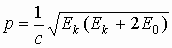 |
| Полная энергия частицы в прямоугольной яме шириной l |  |
Примеры решения задач
Пример 17. Кинетическая энергия электрона равна 1,02МэВ. Вычислить длину волны де Бройля этого электрона.
Дано: Ек = 1,02МэВ = 16,2·10-14Дж; Е0 = 0,51МэВ = 8,1·10-14 Дж
Найти: λ
Решение: Длина волны де Бройля определяется по формуле
где λ - длина волны, соответствующая частице с импульсом р; h -постоянная Планка. По условию задачи кинетическая энергия электрона больше его энергии покоя:
следовательно, движущийся электрон является релятивистской частицей. Импульс релятивистских частиц определяется по формуле
или учитывая соотношение (2),
Подставляя (4) в (1), получим 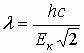
Производя вычисления, получим
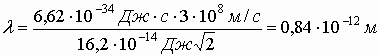
Ответ: λ
=0,84·
10-12м.
Пример 18. Используя соотношения Гейзенберга, показать, что ядра атомов не могут содержать электронов. Считать радиус ядра равным 10-15м
Дано: Rя = 10-15 м; h = 6,62·10-34Дж·с
Найти: Δ
vx
Решение: Соотношение неопределенностей Гейзенберга выражается формулой:  , ,
где Δх – неопределенность координаты; Δрх – неопределенность импульса; h – постоянная Планка. Если неопределенность координаты принять равной радиусу ядра, т.е. Δx = Rя; то неопределенность импульса электрона выразим следующим образом: 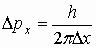 . Так как . Так как  , то , то  и и 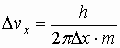 . Вычислим неопределенность скорости электрона: . Вычислим неопределенность скорости электрона:
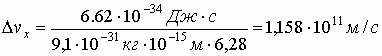
Сравнивая полученное значение Δ
ν
x со скоростью света в вакууме с = 3·108м/с, видим , что Δ
ν
x >c, а это не возможно, следовательно, ядра не могут содержать электронов.
Ответ: ядра не могут содержать электронов.
Пример 19. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности?
Дано: l; ω
n=ω
±
; n = 2
Найти: x
Решение: Волновая функция, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме шириной l, имеет вид
где n – номер энергетического уровня (n=1,2,3...); х – координата частицы в яме (0£x£l). Согласно физическому смыслу волновой функции,
где ω – плотность вероятности обнаружения частицы в точке с координатой х. Если частица находится на втором энергетическом уровне (n=2), то
В соответствии с принципом соответствия Бора выражение для классической плотности вероятности получается при n → ∞:
Приравнивая по условию задачи выражения (3) и (4), получаем
Решая уравнение (5), находим
В пределах потенциальной ямы (0£x£l) таких точек четыре:
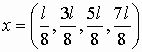
Ответ: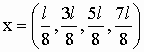 . .
Задачи для самостоятельного решения
301. Электрон прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля для двух случаев: 1)U1=51В; 2)U2=510кВ.
302. Вычислить длину волны де Бройля электрона, движущегося со скоростью v = 0,75с (с - скорость света в вакууме).
303. Определить кинетическую энергию протона и электрона, для которых длины волн де Бройля равны 0,06нм.
304. Какой кинетической энергией должны обладать протоны, чтобы дебройлевская длина волны протона была равна его комптоновской длине волны?
305. Кинетическая энергия протона равна его энергии покоя. Вычислить длину волны де Бройля для такого протона.
306. Протон обладает кинетической энергией, равной энергии покоя. Во сколько раз изменится длина волны де Бройля протона, если его кинетическая энергия увеличится в 2 раза?
307. Кинетическая энергия электрона равна энергии покоя. Вычислить длину волны де Бройля для такого электрона.
308. Масса движущегося электрона в 2 раза больше массы покоя. Определить длину волны де Бройля для такого электрона.
309. Какой кинетической энергией должен обладать электрон, чтобы дебройлевская длина волны электрона была равна его комптоновской длине волны?
310. Определить длины волн де Бройля электрона и протона, прошедших ускоряющую разность потенциалов 400В.
311. Среднее время жизни возбужденных состояний атома 10нс. Вычислить естественную ширину спектральной линии (λ=0,7мкм), соответствующую переходу между возбужденными уровнями атома.
312. Кинетическая энергия электрона в атоме водорода составляет величину порядка 10эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома.
313. Среднее время жизни возбужденного состояния атома равно 12нс. Вычислить минимальную неопределенность длинны волны λ=0,12мкм излучения при переходе атома в основное состояние.
314. Среднее время жизни π0-мезона равно 1,9·10-16с. Какова должна быть энергетическая разрешающая способность прибора, с помощью которого можно зарегистрировать π0-мезон?
315. На фотографии, полученной с помощью камеры Вильсона, ширина следа электрона составляет 0,8·10-3м. Найти неопределенность в нахождении его скорости.
316. Средняя кинетическая энергия электрона в невозбужденном атоме водорода 13,6эВ. Используя соотношение неопределенностей, найти наименьшую погрешность, с которой можно вычислить координату электрона в атоме.
317. Электрон, движущийся со скоростью 8·106м/с, зарегистрирован в пузырьковой камере. Используя соотношение неопределенностей, найти погрешность в измерении скорости электрона, если диаметр образовавшихся пузырька в камере 1мкм.
318. Показать, что для частицы, неопределенность координаты которой 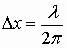 (λ – длина волны де Бройля), неопределенность ее скорости равна по порядку величины самой скорости частицы. (λ – длина волны де Бройля), неопределенность ее скорости равна по порядку величины самой скорости частицы.
319. Среднее время жизни π+-мезона равно 2,5·10-8с. . Какова должна быть энергетическая разрешающая способность прибора, с помощью которого можно зарегистрировать π+-мезон?
320. Атом испустил фотон с длиной волны 0,55мкм. Продолжительность излучения 10нс. Определить наибольшую погрешность, с которой может быть изменена длина волны излучения.
321. Определить ширину одномерной потенциальной ямы с бесконечно высокими стенками, если при переходе электрона с третьего энергетического уровня на второй излучается энергия 1эВ.
322. Частица в потенциальной яме шириной l находится в возбужденном состоянии. Определить вероятность нахождения частицы в интервале 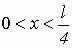 на втором энергетическом уровне. на втором энергетическом уровне.
323. Определить, при какой температуре дискретность энергии электрона, находящегося в одномерной потенциальной яме, ширина которой 2·10-9м, становится сравнимой с энергией теплового движения.
324. Электрон находится в одномерной потенциальной яме с бесконечно высокими стенками, ширина которой 1нм. Определить наименьшую разность энергетических уровней электрона.
325. Электрон находится в одномерной потенциальной яме с бесконечно высокими стенками, ширина которой 1,4·10-9м. Определить энергию, излучаемую при переходе электрона с третьего энергетического уровня на второй.
326. Электрон находится в основном состоянии в одномерной потенциальной яме с бесконечно высокими стенками, ширина которой 0,1нм. Определить силу давления, оказываемую электроном на стенки ямы.
327. Электрон находится в основном состоянии в одномерной потенциальной яме с бесконечно высокими стенками, ширина которой 0,1нм. Определить импульс электрона.
328. Определить, при какой ширине одномерной потенциальной ямы дискретность энергии электрона, становится сравнимой с энергией теплового движения при температуре 300К.
329. Вычислить отношение вероятностей нахождения электрона на первом и втором энергетических уровнях одномерной потенциальной ямы, ширина которой l, в интервале 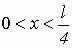 . .
330. Частица в потенциальной яме шириной l находится в возбужденном состоянии. Определить вероятность нахождения частицы в интервале  на третьем энергетическом уровне. на третьем энергетическом уровне.
Качественные задачи
331. Сравните дины волн де Бройля для электрона и шарика массой m=1г, если их скорости одинаковы и равны v=100м/с.
332. Как исходя из соотношения неопределенностей объяснить наличие естественной ширины спектральных линий?
333. Что определяет квадрат модуля волновой функции?
334. Какова наименьшая энергия частицы в "потенциальной яме" с бесконечно высокими "стенками"?
335. Больше или меньше энергия частицы, находящейся в "потенциальной яме" с бесконечно высокими "стенками" в состоянии с n=3 по сравнению с состоянием с n=1?
336. Может ли частица находиться на дне "потенциальной ямы"? Определяется ли это формой "ямы"?
337. Зависит ли распределение энергетических уровней от формы "потенциальной ямы"?
338. Можно ли, пользуясь соотношением неопределенностей, по известному импульсу фотона определить область его локализации?
339. Может ли атом водорода поглотить фотон, энергия которого превосходит энергию связи атома?
340. При какой скорости кинетическая энергия частицы равна ее энергии покоя?
341. Применив к атому модель частицы в потенциальной яме, определить минимальную энергию электрона в атоме. Размеры атома принять равными 10-10м.
342. Оцените энергию электрона для того, что бы он попал в ядро.
343. Объясните физический смысл соотношения неопределенности для энергии E и времени t.
344. Применяя соотношение неопределенностей, покажите, что для движущейся частицы, неопределенность координаты которой равна длине волны де Бройля, неопределенность скорости равна по порядку величины самой скорости частицы.
345. Объясните, почему физический смысл имеет не сама ψ-функция, а квадрат ее модуля |ψ|2?
346. Объясните, почему волновая функция должна быть конечной, однозначной и непрерывной.
347. Известно, что свободная квантовая частица описывается плоской монохроматической волной де Бройля. Плотность вероятности (вероятность, отнесенная к единице объема) обнаружения свободной частицы |ψ|2 = |A|2 = const. Объясните, что означает постоянство этой величины.
348. Электрон находится в одномерной бесконечно глубокой потенциальной яме шириной A в состоянии с минимальной энергией. Каким образом будет изменяться плотность вероятности обнаружения электрона в центре ямы с ростом энергии электрона?
349. Что является решением уравнения Шредингера?
350. Свободная частица в квантовой механике описывается плоской монохроматической волной с амплитудой А. Чему равна вероятность обнаружить частицу в точке пространства с координатами х,у,z?
Контрольные вопросы
- Приведите формулу де Бройля.
- Каковы свойства волн де Бройля?
- Физический смысл соотношений неопределенностей Гейзенберга.
- С какой степенью точности можно говорить о траекториях микрочастиц?
- Приведите соотношение неопределенностей для энергии и времени.
- Статистический смысл волновой функции.
- Что означает условие нормировки волновой функции?
- Запишите уравнение Шредингера для стационарных состояний.
- Запишите формулу энергии частицы в "потенциальной яме" с бесконечно высокими "стенками".
- Что определяет главное квантовое число?
- Как определить вероятность нахождения частицы в некотором интервале?
- Записать уравнение Шредингера для стационарных состояний электрона, находящихся в атоме водорода.
- Условия, при которых уравнение Шредингера для стационарных состояний электрона в атоме водорода, имеет решение.
- Что характеризуют квантовые числа?
- Почему квантовая механика является статистической теорией?
- Сформулируйте принцип причинности в квантовой механике.
- Какие спектры излучения дают атомы водорода?
- Что такое энергетический уровень?
- Что называют потенциалом ионизации?
- От чего зависит энергия электрона в атоме водорода?
- Когда атом поглощает и излучает энергию?
|