Методические указания к выполнению графической работы
«Аксонометрические проекции»

§ 4. Прямоугольная диметрия

Прямоугольная диметрия характеризуется тем, что коэффициенты искажения, определенные из выражения (1), u = w = 0,94, a v = 0,47. Определяют их следующим образом:

u² + (u/2)² + u² = 2;
u² = 8/9; u = w = √8/9 ≈ 0,94; v = 0,47.

В соответствии с ГОСТ 2.317-69 практические построения в прямоугольной диметрии следует выполнять пользуясь приведенными коэффициентами искажения: u = w = 1 и v = 0,5.

Расположение осей стандартной прямоугольной диметрии показано на рис. 8.

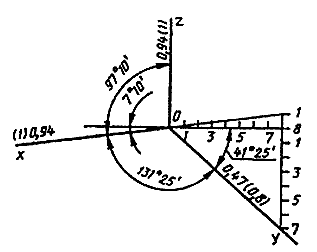
Рис. 8

Аксонометрический масштаб для прямоугольной диметрии будет М^А 1,06:1.

В прямоугольной диметрии равные окружности диаметра d, лежащие в координатных плоскостях х0у и у0, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а малая - 2b = 0,35d, если пользуемся приведенными коэффициентами искажения. Окружность, расположенная в плоскости xOz, проецируется эллипс с осями: большая ось 2а' = 1,066d, малая ось 2b' = 0,95d (рис. 9).

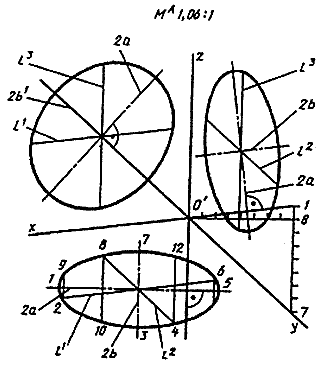
Рис. 9

Диаметры окружности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диметрии l¹ = l² = d; l = 0,5d, при этом l¹ ׀׀ Ox; l² ׀׀ Oу; l³ ׀׀ Oz.

Кроме указанных,можно построить еще четыре точки, симметричные точкам, ограничивающим проекции диаметров, параллельных координатным осям. Тогда эллипсы, как диметрию окружности, можно построить по его двенадцати точкам.

Изображение геометрических поверхностей в прямоугольной диметрии рассмотрим на примере построения стандартной прямоугольной диметрии прямого кругового цилиндра. На рис. 10 приведен пример комплексного чертежа полого цилиндра высотой Н с наружным d и внутренним d₁ диаметрами. Цилиндр расположим в натуральную величину в натуральной системе координат Oxyz, относительно которой построим диметрическую его проекцию.

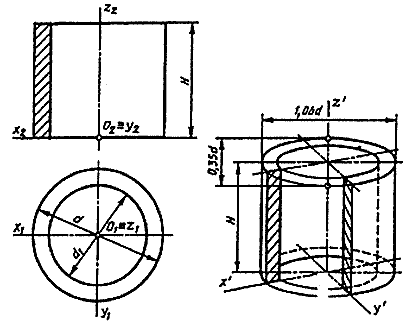
Рис. 10

Как и в случае построения окружностей в изометрии, в диметрии также начнем построение фигуры с эллипсов верхнего и нижнего оснований цилиндра, которые являются изометрическими проекциями окружностей этих оснований. Окружности оснований расположены в плоскостях, параллельных горизонтальной плоскости проекций, поэтому, пользуясь приведенными ранее правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz. Малые оси эллипсов совпадут с направлением оси Oz, Центры осей эллипсов нижнего и верхнего оснований расположены на расстоянии Н. Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров. Построив эллипсы, приведем очерковые линии, касательные к внешним эллипсам. Для наглядности построим вырез четверти цилиндра, построение которого видно из (рис. 10). Невидимые линии покажем штриховыми линиями. Для наглядности такими же линиями покажем линии вырезанной части цилиндра. Видимые контурные линии наводят нужной толщиной.