Тема №12 Взаимное пересечение поверхностей. Способ сфер

1. Способ сфер

2. Частные случаи взаимного пересечения поверхностей. Теорема Монжа

Контрольные вопросы

Контрольные задания по теме:
Рабочая тетрадь задача 75, задача 76

1. Способ сфер

Этот метод вытекает из свойств, присущих поверхностям вращения: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей. На рисунке 54 показано сечение конуса и цилиндра вспомогательной сферой.

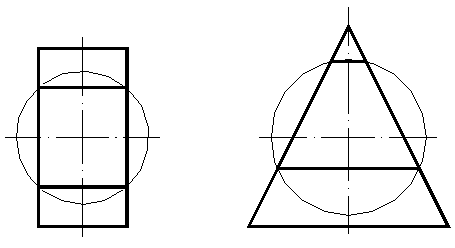
Рисунок 54

Способ сфер применяется в особом случае, когда поверхности вращения расположены так, что их оси пересекаются и параллельны одной из плоскости проекций.

Построение линии пересечения поверхностей вращения с помощью вспомогательных секущих сфер возможно двумя способами:

1) способом концентрических сфер;

2) способом эксцентрических сфер.

Первый применяется тогда, когда оси поверхностей - прямые линии, а второй - когда одна из осей является кривой.

Рассмотрим пример пересечения двух цилиндров разного радиуса. Оси их пересекаются и параллельны фронтальной плоскости проекций. Поверхности изображены на рисунке 55.

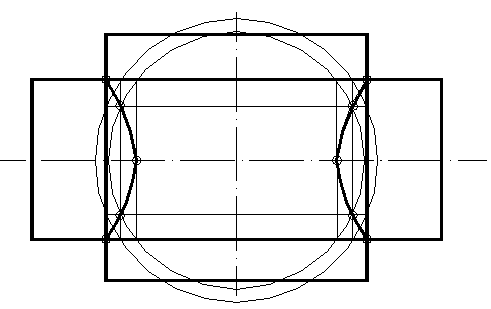
Рисунок 55

Первая сфера проводится так, чтобы она была вписана в поверхность большего диаметра, последующие сферы пересекают обе поверхности, а радиус последней сферы равен расстоянию до точек пересечения очерков.

Вспомогательные сферы пересекают цилиндры по окружностям, которые проецируются в прямые линии, проходящие через точки пересечения сфер с очерками цилиндров. Точки пересечения этих прямых и есть общие точки для двух поверхностей.

При построении линии пересечения этим способом все сферы проводятся из одного центра, которым является точка пересечения осей. В способе эксцентрических сфер центр секущей сферы передвигается вдоль оси поверхности, ось которой прямолинейна.

2. Частные случаи взаимного пересечения поверхностей. Теорема Монжа

Если две пересекающиеся поверхности вращения можно описать вокруг третьей, то линия пересечения в этом случае распадется на две плоские кривые. Примеры такого пересечения приведены на рисунке 56.

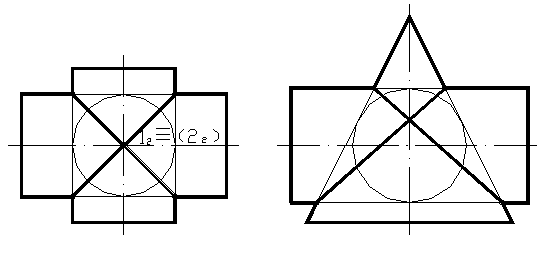
Рисунок 56

В рассмотренных примерах имеет место двойное соприкасание пересекающихся поверхностей второго порядка. Эти поверхности могут быть описаны вокруг одной сферы. Данный случай относится к частным случаям взаимного пересечения поверхностей и описывается теоремой Монжа: две поверхности второго порядка, описанные около третьей поверхности второго порядка (или в нее вписанные), пересекаются между собой по двум кривым второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

Контрольные вопросы

1. Какое свойство поверхностей вращения лежит в основе способа сфер?

2. При каком расположении поверхностей возможно применение способа сфер для построения линии их взаимного пересечения?

3. В каком случае следует применять метод эксцентрических сфер, а в каком – концентрических?

4. Какие частные случаи пересечения поверхностей вы знаете?

5. Сформулируйте теорему Монжа.