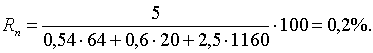8. Пример выполнения расчетной части проекта
8.3. Оптимизация запасов ресурсов в условиях
узкой специализации работы предприятия
Основной задачей закупочной логистики является полное использование имеющихся ресурсов с целью получения максимальной прибыли. Очевидно, что с экономической точки зрения целесообразно реализовать излишние ресурсы и на вырученные средства закупить дефицитные. Однако и это не гарантирует получение максимального экономического эффекта (максимальной прибыли, минимальных затрат на хранение и пр.).
Использование двойственного симплекс-метода показывает преимущества изменения одного ограничения по отношению к другим. Пусть, например, в приведенной задаче двойственная оценка по первому ограничению оказалась выше, чем по второму. Следовательно, увеличение запасов первого ресурса за счет реализации второго позволит улучшить результаты решения. Очевидно, что в данном случае оптимальное решение будет лежать на оси Х1.
Таким образом, задача оптимизации величины запасов ресурсов не должна заканчиваться на этапе, характеризующемся отсутствием их излишков. Ее решение должно продолжаться путем реализации некоторой части ресурсов, приносящих меньшую прибыль с целью приобретения ресурсов, более ценных с точки зрения целевой функции.
Увеличение запасов одного вида ресурсов за счет остальных в пределе приводит к выпуску только одного вида изделия, дающего наибольшую прибыль. Такая узкая специализация позволяет разработать самую простую типовую схему движения предметов труда, минимизировать внутрипроизводственные связи, уменьшить простои оборудование и пролеживание предметов труда, улучшить качество продукции и пр. В таком случае математическая модель задачи упрощается и принимает вид:
где r – номер наиболее рентабельной продукции;
Xr – количество наиболее рентабельной продукции;
Pk – прибыль от реализации этой продукции.
Эта задача состоит не только в определении объема выпуска продукции Xr, но и в определении величины запасов необходимых для этого ресурсов Ci. С учетом того, что все запасы должны быть израсходованы полностью, они должны быть пропорциональны их нормам расхода. При изменении запаса одного ресурса соответствующим образом должны быть изменены и запасы других ресурсов, потребляемых при производстве данных видов продукции. Запасы ресурсов, естественно, должны быть пропорциональны нормам их расхода:
или с учетом (8.1)
Суммарная стоимость используемых ресурсов
где di – стоимость единицы ресурса i-того вида.
С учетом (8.1)
Отсюда легко определяется Xr:
и по (8.2) необходимые для этого запасы ресурсов в пределах имеющихся финансовых возможностей.
В условиях острой конкурентной борьбы и с учетом возможного насыщения рынка такой подход далеко не всегда допустим, в связи с чем в математическую модель приходится вводить соответствующие дополнительные ограничения вида:
где Xk;max – максимально возможный объем реализации k-того вида продукции;
Xg;min – минимально допустимый объем выпуска g-того вида продукции.
В первом случае Xk оказывается заданным. На производство этого вида продукции потребуются определенные деньги. Тогда задача сводится к определению количества второго по рентабельности вида продукции Xk2 по формуле:
где 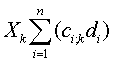 – затраты на предельно допустимый объем выпуска наиболее рентабельной продукции. – затраты на предельно допустимый объем выпуска наиболее рентабельной продукции.
Если же в силу некоторых обстоятельств выпуск некоторого вида продукции ограничен снизу, то
где 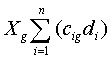 – затраты на производство обязательной продукции. – затраты на производство обязательной продукции.
Обобщая формулы (8.10) и (8.11) для любого числа ограничений сверху и снизу на выпуск продукции, можно получить формулу, позволяющую определять объем наиболее рентабельной продукции из числа тех, на которые данные ограничения не распространяются:
где m – количество видов продукции, на объем производства которых наложены ограничения.
При этом запасы ресурсов должны вычисляться по формуле:
Применение этих формул позволяет оптимизировать запасы ресурсов, свести к минимуму затраты, связанные с их хранением, и обеспечивает выпуск наиболее рентабельной продукции при выполнении всех наложенных ограничений.
8.3.1. Пример решения задачи оптимизации
запасов ресурсов в условиях узкой
специализации работы предприятия
Определим рентабельность производства крупного рогатого скота и птицы как частное от деления прибыли на затраты на производство единицы продукции. В расчете рентабельности учитываем только затраты на приобретение ресурсов.
В данной задаче рентабельность производства крупного рогатого скота составляет:

рентабельность производства птицы:
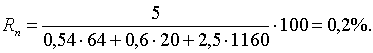
Таким образом, в данном случае выращивание коров оказывается значительно выгоднее.
Определим имеющиеся денежные средства, вложенные в ресурсы:
1050×25+600×64+20×60+500×70+1160×7300=8568850 у.е.
Эти деньги целесообразно вложить только в выращивание коров.
Количество коров определяем из выражения:
2,1×25×Х1+1×64×Х1 +1×70×Х1+10,5×1160×Х1=8568850,
откуда
Х1= 8568850/(2,1×25+1×64+1×70+10,5×1160)= 703.
Тогда запасы ресурсов могут быть найдены из исходной модели при Х2=0:
Силоса 2,1×703 = 1476,3 т;
Комбикорма 703 т;
Зерна 0,6×703=422 т;
Выпаса 703 га;
Затраты трудовых ресурсов 10,5×703 =7381 чел.-дней
При этом будет получена прибыль в размере
F=160×703=112480 у.е.
В качестве графической иллюстрации на рис. 8.9 приведено графическое решение этой задачи.

Рис. 8.9. Графическое решение задачи в условиях узкой специализации
| 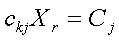


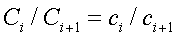
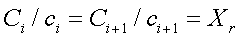
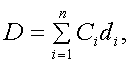

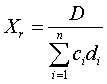
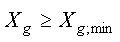
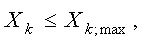
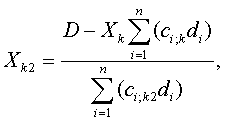
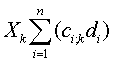 – затраты на предельно допустимый объем выпуска наиболее рентабельной продукции.
– затраты на предельно допустимый объем выпуска наиболее рентабельной продукции.

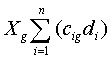 – затраты на производство обязательной продукции.
– затраты на производство обязательной продукции.