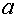и функция
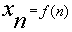натурального аргумента. Тогда говорят, что это число 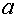называется пределом последовательности 
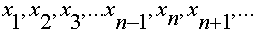или пределом функции натурального аргумента, если для сколь угодно малого произвольно выбранного положительного числа 
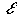можно найти такое натуральное число 
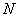, что при любом 
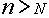выполняется неравенство 
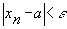,т.е. отклонение функции 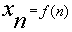от предела 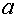, равное 
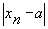должно быть меньше 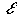.Если функция
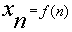стремится к пределу 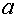при 
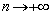, то это записывается так: 
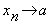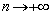приили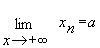
.
Если последовательность имеет предел, то она называется сходящейся, если последовательность предела не имеет, то она называется расходящейся.
