Предел функции действительного переменного
Пусть функция определена в некотором промежутке, содержащем точку 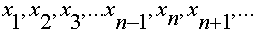 .
.
Пусть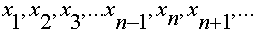 ,произвольная последовательность значений аргумента из области определения данной функции, которая стремится к данному числу
,произвольная последовательность значений аргумента из области определения данной функции, которая стремится к данному числу 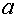 .
Этой последовательности
.
Этой последовательности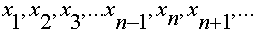 будет соответствовать некоторая последовательность значений самой функции
будет соответствовать некоторая последовательность значений самой функции 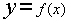 :
:
 ,
,  ,
, ┘.. ( 2 )
┘.. ( 2 )
Если любая последовательность ( 2 ) имеет своим пределом число 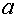 , то оно и будет пределом функции
, то оно и будет пределом функции 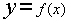 при
при 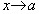 .
.
Число 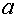 называется пределом функции
называется пределом функции 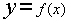 , т.е.
, т.е.  , если для сколь угодно малого положительного числа
, если для сколь угодно малого положительного числа 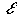 можно найти такое число
можно найти такое число 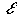 , что для
, что для
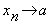 выполняется неравенство
выполняется неравенство
 .
.
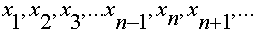 .
.
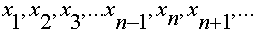 ,произвольная последовательность значений аргумента из области определения данной функции, которая стремится к данному числу
,произвольная последовательность значений аргумента из области определения данной функции, которая стремится к данному числу 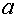 .
Этой последовательности
.
Этой последовательности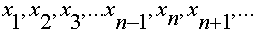 будет соответствовать некоторая последовательность значений самой функции
будет соответствовать некоторая последовательность значений самой функции 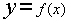 :
:
 ,
,  ,
, ┘.. ( 2 )
┘.. ( 2 )
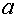 , то оно и будет пределом функции
, то оно и будет пределом функции 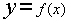 при
при 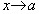 .
.
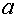 называется пределом функции
называется пределом функции 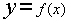 , т.е.
, т.е.  , если для сколь угодно малого положительного числа
, если для сколь угодно малого положительного числа 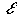 можно найти такое число
можно найти такое число 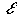 , что для
, что для
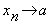 выполняется неравенство
выполняется неравенство
 .
.