



ПЛАН:
Суждение - это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком или отношение между предметами.
Любое суждение может быть расценено как истинное (соответствующее действительности) или ложное
Языковой формой суждения является повествовательное предложение (косвенно суждение содержит и риторический вопрос, поскольку он по смыслу является утверждением или отрицанием).
Предложения в других грамматических формах (собственно вопросительные, побудительные и т.д.) непосредственно суждениями не являются, поскольку ничего не утверждают и не отрицают.
Полная структура простого суждения включает четыре элемента:
субъект (S) - понятие, отражающее сам предмет мысли, то, о чем что-то говорится;
предикат (Р) - понятие, отражающее то, что именно говорится о предмете (его свойство или соотношение с другими объектами);
связка (в языковой форме выражается словами "есть/не есть", "суть/не суть, "является/не является" и т.п., либо вообще только подразумевается). Отражает наличие /отсутствие определенной связи субъекта и предиката;
квантор (всеобщности (") - "все", "каждый", "ни один… не" ("все … не") и т. п.; существования ($) - "некоторые", "многие", "часть" и т. п.; единственности существования ($!) - "этот", "данный" и т. п.), отражающий количественную характеристику суждения.
Символически структура простого суждения выражается формулой: (K)S-P, где <К> - некоторый квантор, а <-> - связка (если квантор отсутствует в явном виде, то суждение формально неопределенно по количеству, хотя эту характеристику обычно можно установить по смыслу).
Простые суждения подразделяются по качеству на: утвердительные и отрицательные, а по количеству на:
единичные (что-либо утверждается или отрицается об одном предмете - "Этот свидетель дал показания");
общие (что-либо утверждается или отрицается обо всех предметах некоторого класса - "Все свидетели дали показания");
частные (что-либо утверждается или отрицается о части предметов некоторого класса - "Некоторые свидетели дали показания").
Особое место в классификации суждений по количественной характеристике занимают выделяющие и исключающие суждения.
Выделяющие суждения выражают тот факт, что признак, выраженный предикатом, принадлежит (не принадлежит) только данному предмету.
Выделяющие суждения могут быть единичными, частными и общими, например: "Только Иванов написал эту контрольную на отлично" - выделяющее единичное суждение, "Некоторые учащиеся (и только учащиеся) являются школьниками" - выделяющее частноутвердительное суждение,
"Все квадраты (и только квадраты) являются прямоугольными ромбами" - выделяющее общеутвердительное суждение (определение).
Исключающим называется суждение, в котором отражается принадлежность (или непринадлежность) признака всем предметам, за исключением некоторой их части. Например: "Все студенты нашей группы, кроме Иванова, сдали зачет по логике".
Исключающие суждения выражаются предложениями со словами "кроме", "за исключением", "помимо", "не считая" и т.п.
Значение выделяющих и исключающих суждений состоит в том, что содержащиеся в них мысли не допускают их неоднозначного понимания. Именно поэтому ряд научных положений, а также законов государства, статей Конституции, уголовно-процессуального и других кодексов выражен в этой логической форме.
По характеру предиката различают суждения:
атрибутивные. Атрибутивным называется суждение о признаке предмета, например: "Лист зеленый";
с отношением. Релятивным называется суждение об отношении между предметами. Например, "Москва больше Красноярска";
существования. В суждениях существования выражается сам факт существования или несуществования предмета суждения. Например: "Высшее образование есть".
Объединяя количественную и качественную характеристики, суждения делятся на:
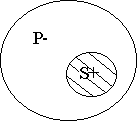
общеутвердительные (А) - "Все S есть Р",
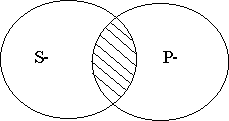
частноутвердительные (I) - "Некоторые S есть Р",
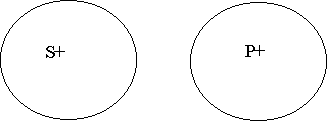
общеотрицательные (Е) - "Ни один S не есть Р",
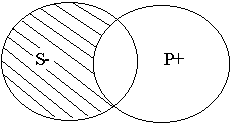
частноотрицательные (О) - "Некоторые S не есть Р"
В Средние века были приняты эти буквенные обозначения по первым гласным латинских слов affirmo - утверждаю и nego - отрицаю.
Термин считается распределенным (обозначается"+"), если он взят в полном объеме. Термин считается нераспределенным (обозначается"-"), если он взят в части объема.
Несравнимыми среди простых суждений являются суждения, имеющие различные субъекты или предикаты.
Сравнимыми являются суждения с одинаковыми субъектами и предикатами.
Для иллюстрации отношений между простыми суждениями используется
логический квадрат:
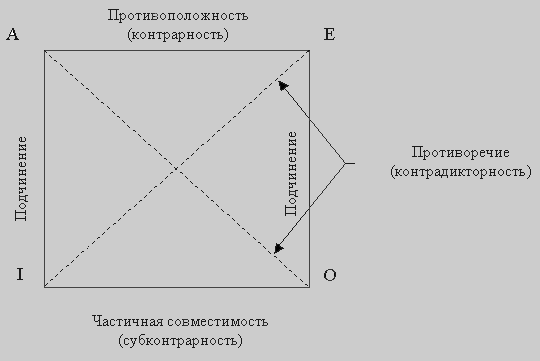
Среди сравнимых различают совместимые суждения, которые могут быть одновременно истинными, и несовместимые суждения, которые одновременно истинными быть не могут.
Совместимость бывает трех видов: полная совместимость (эквивалентность); подчинение; частичная совместимость (субконтрарность).
Несовместимость бывает двух видов: противоположность (контрарность) и противоречивость (контрадикторность).
I. Отношением подчинения связаны суждения А и I, Е и О. Общие суждения (А и Е) являются подчиняющими, а частные (I, О) подчиненными. Для суждений находящихся в отношении подчинения, имеет значение условие истинности: Если истинно А(Е), то истинно и I(O), но не наоборот.
II. Отношением противоречия связаны суждения Е и I, А и О. Два противоречивых суждения (согласно законам логики) не могут быть одновременно ни истинными, ни ложными
Если А - истинно, то О - ложно
Если А - ложно, то О - истинно
Если О - истинно, то А - ложно
Если О - ложно, то А - истинно
Если Е - истинно, то I - ложно
Если Е - ложно, то I - истинно
Если I -истинно, то E - ложно
Если I - ложно, то E - истинно
III. Отношением контрарности (противоположности) связаны только общие суждение А и Е. Закон исключения третьего к таким суждениям не применим. А и Е могут оказаться одновременно ложными, но не могут быть одновременно истинными (пример: оба суждения "Все любят логику" и "никто не любит логику" - ложны).
IV. Отношение субконтрарности существует между частными суждениями I и О. I и О могут быть одновременно истинными, но не могут быть одновременно ложными (пример: оба суждения "Некоторые люди любят логику" и "некоторые люди не любят логику" - истинны)
4. Операции с простыми суждениями (непосредственные умозаключения).
При помощи операций обращения, превращения и противопоставления получаются новые суждения, эквивалентные исходным.
Смысл обращения как операции заключается в том, что субъект и предикат суждения меняются местами (обращаются), не меняя качества суждения.
Если количество при этом сохраняется, то это суждение без ограничения (простое или чистое), если количество исходного суждения меняется, то это суждение с ограничением.
I. A→I
Суждение А обращается в I с ограничением (ограничение связано с тем что понятия S и Р взяты в разном объеме, в этом легко убедится при помощи схемы).
Все S есть Р
Некоторые Р есть S
Например: "Если все люди смертны,
то лишь некоторые смертные существа являются людьми" (Если все S есть Р, то некоторые Р есть S).
Возможно обращение А→А: Если все квадраты(S) являются равносторонними прямоугольниками, то все равносторонние прямоугольники(P) являются квадратами (S) (Если все S есть Р, то все Р есть S)
II. Е→Е
Суждение Е обращается в Е без ограничения
Например: "Если все театры не являются поликлиниками, то все поликлиники не являются театрами".
Все S не-есть Р
Все Р не-есть S
III. I→I
Суждения I обращается в I также без ограничения.
Некоторые S есть Р
Некоторые Р есть S
Например: Если некоторые студенты являются спортсменами, то некоторые спортсмены являются студентами
IV. О→?
Суждение О не обращается
Превращение - преобразование некоторого категорического суждения в противоположное по качеству и с предикатом, противоречащим исходному предикату.
Чтобы выполнить превращение, необходимо:
1) заменить связку исходного суждения на противоположную по качеству (т. е. "есть" на "не есть", и наоборот)
2) заменить предикат исходного суждения на противоречащий (т. е. Р на не-Р или не-Р на Р)
Превращать можно категорические суждения всех видов: 1. А в Е: Все дети любопытны Ни один ребенок не является нелюбопытным 2. Е в А: Ни один человек не является совершенным Все люди являются несовершенными 3. I в О: Некоторые студенты ленивы Некоторые студенты не являются неленивыми 4. О в I: Некоторые студенты не являются примерными Некоторые студенты являются непримернымиВ превращении утвердительные суждения преобразуются в отрицательные, и наоборот и в результате получается суждение эквивалентное исходному.
Противопоставление - лог. операция с простыми суждениями, производящая одновременно и обращение и превращение суждений. Если происходит сначала обращение, а потом превращение, то это противопоставление субъекту Если происходит сначала превращение, а потом обращение, то противопоставление предикату.
1. А в О
Все студенты учащиеся - исходное суждение
Некоторые учащиеся - студенты - обращение исходного сужд.
Некоторые учащиеся не являются не студентами - превращение
обращенного cужд.
2. Е в А
Ни один врач не является юристом
Все юристы не являются врачами
Все юристы являются не врачами
3. I в О
Некоторые студенты являются отличниками
Некоторые отличники являются студентами
Некоторые отличники не являются нестудентами
4. Частноотрицательные суждения (О) путем противопоставления субъекту, в силу неопределенности квантора "некоторые", не позволяют указать единственное следствие из исходного суждения.
1. А в Е Все звезды являются небесными телами - исходное суждение Все звезды не являются ненебесными телами - превращение Все ненебесные тела не являются звездами - обращение 2. Е в I Ни один ребенок не является взрослым Все дети являются не взрослыми Некоторые невзрослые являются детьми 3. О в I Некоторые животные не являются млекопитающими Некоторые животные являются не млекопитающими Некоторые не млекопитающие являются животными
4.Частноутвердительные суждения (О) путем противопоставления предикату, в силу неопределенности квантора "некоторые", не позволяют указать единственное следствие из исходного суждения.

