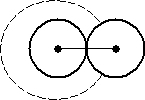
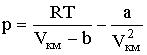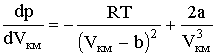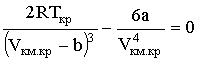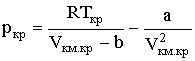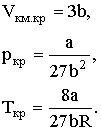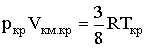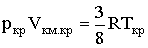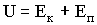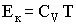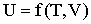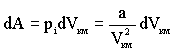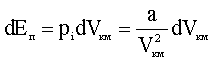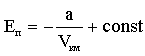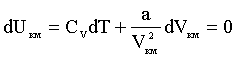где р - давление, оказываемое на газ извне и равное давлению газа на стенки сосуда, а и b - константы Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем. В системе СИ константа а измеряется в Н·м4/кмоль2, константа b - в м³/кмоль. Константа b определяет ту часть объема, которая недоступна для движения молекул вследствие их конечных размеров, и равна учетверенному объему молекулы. Пусть в сосуде находится только две молекулы. Центр любой из них не может приблизиться к центру другой на расстояние, меньшее диаметра молекулы d (Рис. 2.2.1).
Таким образом, для центра этой молекулы оказывается недоступным сферический объем с радиусом d, т.е. объем, равный 8 объемам молекулы. Поскольку принято во внимание парное взаимодействие молекул, в расчете на одну молекулу недоступным оказывается объем, равный учетверенному объему молекулы. В газе молекулы взаимодействуют (сталкиваются) чаще всего попарно, поскольку вероятности столкновения трех и более молекул крайне малы, поэтому приведенное рассуждение справедливо для всего объема газа: константа b равна учетверенному суммарному объему всех молекул. Фактически введением константы b учитывают отталкивание между молекулами, возникающее при их сильном сближении. Кроме сил отталкивания, между молекулами есть и силы притяжения. Поправка
Коэффициент пропорциональности а должен быть измерен, поскольку нет способа точного его вычисления. Чтобы перейти к произвольной массе газа, учтем, что z = m/μ киломолей газа при тех же условиях занимают в z раз больший объем: V = z·Vкм. Используя это обстоятельство, запишем уравнение (2.2.1) так:
Умножив это уравнение на z и вводя обозначения:
придем к уравнению Ван-дер-Ваальса для произвольной массы газа:
Насколько уравнение Ван-дер-Ваальса лучше описывает поведение реальных газов, чем уравнение состояния идеального газа, можно судить по данным для 1 л газообразного азота, занимающего при нормальных условиях объем 1 л при 0°С (Табл. 2.2.1). Таблица 2.2.1
Как видно из Табл. 2.2.1, уравнение Ван-дер-Ваальса гораздо лучше согласуется с экспериментом. Уравнение (2.2.5) можно представить так:
Получилось кубическое уравнение относительно неизвестной V, коэффициенты которого зависят от давления и температуры. Такое уравнение со свободным членом и вещественными коэффициентами имеет три решения, причем в зависимости от соотношения между коэффициентами либо все три решения будут вещественными, либо одно решение - вещественным, а два других - комплексными. Поскольку объем может быть только вещественной величиной, комплексные решения не имеют физического смысла. На Рис. 2.2.2 показаны изотермы Ван-дер-Ваальса для нескольких значений температур.
При температуре Т' и давлениях в пределах p'1 до p'2 коэффициенты в уравнении (2.2.6) таковы, что все три решения оказываются вещественными; при иных давлениях вещественным будет только одно решение. Начиная с определенной, своей для каждого вещества температуры Ткр (критической температуры) при любом давлении вещественным остается только одно решение уравнения (2.2.6). Если повышать температуру, то точки, соответствующие решениям уравнения V'1, V'2, V'3, все больше сближаются, сливаясь при критической температуре в одну точку К, также называемую критической точкой. Для соответствующей изотермы точка К является точкой перегиба. Ей соответствуют три совпадающих вещественных решения уравнения (2.2.6). Касательная к критической изотерме в точке К будет параллельна оси V, так что в этом случае производная Разрешим уравнение (2.2.1) относительно р:
Дифференцирование (2.2.7) по объему дает:
В критической точке, т.е. при подстановке Т = Ткр, Vкм = Vкм.кр, эти выражения должны обращаться в нуль:
Совместно с (2.2.7), записанным для точки К:
они образуют три уравнения с тремя неизвестными ркр, Vкм.кр и Ткр. Решение этой системы уравнений дает:
Таким образом, зная константы Ван-дер-Ваальса а и b, можно найти соответствующие критической точке параметры ркр, Vкм.кр и Ткр, которые называются критическими величинами. И, наоборот, по известным критическим величинам могут быть найдены значения констант Ван-дер-Ваальса. Из (2.2.13) и (2.2.12) можно получить:
в то время как согласно уравнению состояния идеального газа должно было бы выполняться соотношение:
2.2.2. Внутренняя энергия реального газаВзаимодействие между молекулами реального газа обусловливает их взаимную потенциальную энергию, которая должна учитываться во внутренней энергии газа наряду с кинетической энергией движения молекул:
Кинетическая энергия киломоля газа равна:
и прямо пропорционально зависит от температуры. Потенциальная энергия взаимодействия молекул зависит от среднего расстояния между ними, поэтому Еп должна быть функцией объема газа V. Следовательно, внутренняя энергия газа есть функция двух параметров - температуры и объема:
При расширении газа совершается работа по преодолению сил притяжения между молекулами. Работа против внутренних сил, действующих между молекулами киломоля газа, может быть записана в виде:
Приравнивая (2.2.19) приращению потенциальной энергии, получим:
Интегрируя (2.2.20), имеем:
Значение постоянной интегрирования полагают равной нулю, что при увеличении объема газа до бесконечности соответствует отсутствию взаимодействия между молекулами газа. Тогда полное выражение для внутренней энергии киломоля реального газа будет иметь вид:
Из (2.2.22) следует, что внутренняя энергия растет как при повышении температуры, так и при увеличении объема. Если газ будет расширяться или сжиматься без теплообмена с внешней средой и без совершения над ним внешней работы, то, согласно первому началу термодинамики, его внутренняя энергия должна оставаться постоянной. Тогда из (2.2.22) получим:
из чего следует, что приращения dT и dVкм имеют противоположный знак. Следовательно, при расширении в таких условиях газ всегда должен охлаждаться, а при сжатии - нагреваться.
|
описывает поведение реальных газов при не слишком высоких давлениях и при достаточно высоких температурах. В действительности, при давлениях порядка 200 атм наблюдаются значительные отклонения от этого закона, которые, непрерывно возрастая с увеличением давления, достигают при 1000 атм более 100%. При выводе уравнения состояния идеального газа не принимались во внимание размеры молекул и их взаимодействие друг с другом. Между тем при повышении давления возрастает плотность газа, что приводит к уменьшению среднего расстояния между молекулами, вследствие чего размерами молекул и их взаимодействием пренебрегать уже нельзя. Размеры молекулы имеют порядок 10-8 см. Тогда для объема одной молекулы получим:
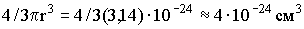
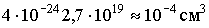
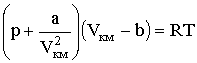
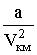дает внутреннее давление pi, обусловленное взаимным притяжением молекул друг к другу. Если бы взаимодействие между молекулами вдруг прекратилось бы, то для того, чтобы удержать газ в пределах заданного объема потребовалось бы увеличить внешнее давление на величину pi. Обратная пропорциональность 
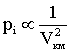может быть объяснена так. Любая молекула, находящаяся вблизи стенки сосуда, будет иметь с одной стороны (обращенной внутрь сосуда) больше соседей, чем с другой. В результате эта молекула будет испытывать результирующую силу, направленную внутрь сосуда. Давление, которое испытывает пристенный слой молекул со стороны остальных молекул газа, равно силе f, действующей на все молекулы на единице поверхности слоя. Очевидно, что эта сила пропорциональна плотности молекул n.
С другой стороны, число молекул N в пристенном слое, испытывающих притяжение, также пропорционально n. Следовательно, pi∼N·∼n2. Так как концентрация молекул обратно пропорциональна объему, занимаемому одним молем газа, то выполняется:
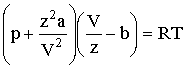
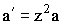
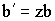
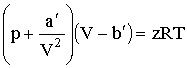
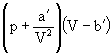, атм·л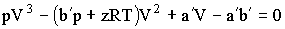
.
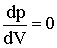Кроме того, в точке перегиба должна быть равна нулю и вторая производная 
.
