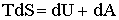При сжатии система совершает работу А2 и отдает тепло Q2, что равносильно получению тепла –Q2. Следовательно,
Складывая уравнения (2.3.1) и (2.3.2), получаем:
Поскольку А1 + А2 есть полная работа А, совершаемая системой за цикл, можно записать:
Периодически действующий двигатель, совершающий работу за счет получаемого извне тепла, называется тепловой машиной. Первое начало термодинамики иногда формулируют так: периодически действующий вечный двигатель (перпетуум мобиле) первого рода, совершающий работу в большем количестве, чем он получает энергии извне, невозможен. Как следует из (2.3.4), не все получаемое извне тепло Q1 используется для получения полезной работы. Для того, чтобы двигатель работал циклами, часть тепла Q2 должна быть возвращена во внешнюю среду и, следовательно, не используется по назначению. Очевидно, что чем полнее тепловая машина превращает получаемое извне тепло Q1 в полезную работу А, тем эта машина выгоднее. Поэтому тепловую машину принято характеризовать коэффициентом полезного действия (КПД), который определяется как отношение совершаемой за цикл работы к получаемому за цикл количеству тепла Q1:
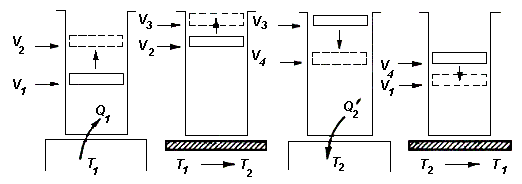
Из определения КПД следует, что он не может быть больше единицы. 2.3.3. Второе начало термодинамикиВторое начало термодинамики, как и первое, может быть сформулировано несколькими способами. В наиболее очевидной формулировке второе начало гласит, что: невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Более строго, невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому. Еще одна формулировка: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращение этого тепла в работу полностью. Работа может быть полностью превращена в тепло, например, посредством трения, обратное неверно. 2.3.4. Цикл КарноПредположим, что какое-либо тело может вступать в теплообмен с двумя тепловыми резервуарами, имеющими температуры Т1 и Т2 и обладающими бесконечно большой теплоемкостью. Это означает, что получение или отдача этими резервуарами конечного количества тепла не изменяет их температуры. Выясним, какой обратимый цикл может совершать тело в таких условиях. Рассматриваемый цикл может состоять как из процессов, в ходе которых тело обменивается теплом с резервуарами, так и из процессов, не сопровождающихся теплообменом с окружающей средой, т.е. происходящих адиабатически. Процесс, сопровождающийся обменом тепла с резервуарами, может быть обратимым только в том случае, если в ходе этого процесса температура тела будет равна температуре соответствующего резервуара. Это - изотермический процесс, протекающий при температуре резервуара. Обратимый цикл, совершаемый телом (или системой), вступающим в теплообмен с двумя тепловыми резервуарами бесконечно большой емкости, будет состоять из двух изотер (при температурах резервуаров) и двух адиабат. Это - цикл Карно. Рассмотрим, как может быть осуществлен цикл Карно с газом в качестве рабочего вещества. Поместим газ в цилиндр, закрытый плотно пригнанным поршнем. Пусть стенки и поршень сделаны из непроводящих тепло материалов, дно цилиндра, напротив, изготовлено из материала с высокой теплопроводностью. Теплоемкость цилиндра и поршня считается бесконечно малой. Пусть первоначально поршень занимает положение, отвечающее объему V1 и температуре газа Т1. Поставим цилиндр на резервуар, имеющий температуру Т1, и предоставим газу возможность очень медленно расширяться до объема V2. При этом газ получит от резервуара тепло Q1 (Рис. 2.3.3).
Затем снимем цилиндр с резервуара, закроем дно теплоизолирующей крышкой и позволим газу расширяться адиабатически до тех пор, пока его температура не упадет до значения Т2. Объем газа в результате станет равным V3. Убрав теплоизолирующую крышку, поставим цилиндр на резервуар, имеющий температуру Т2 и сожмем газ изотермически до такого объема V4, чтобы при последующем адиабатическом сжатии при достижении температуры Т1 объем получил значение V1 (иначе цикл не замкнется). Наконец, снимем цилиндр с резервуара, закроем дно теплоизолирующей крышкой и, сжимая газ адиабатически, приведем его в первоначальное состояние (температура Т1, объем V1). Если газ идеальный, соответствующий цикл на (р-V) диаграмме имеет вид, показанный на Рис. 2.3.4.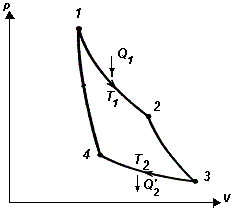 
Рис. 2.3.4. (р-V) диаграмма цикла Карно 2.3.5. КПД цикла Карно для идеального газаРассмотрим цикл Карно для идеального газа. КПД тепловой машины равен:
где Q1 - тепло, получаемое за цикл от нагревателя, Q2 - тепло, отдаваемое за цикл холодильнику. При изотермическом процессе внутренняя энергия идеального газа остается постоянной. Поэтому количество полученного газом тепла Q1 равно работе А12, совершаемой газом при переходе из состояния 1 в состояние 2 (Рис. 2.3.4). Эту работу можно рассчитать так:
Используя уравнение Клапейрона-Менделеева, получим:
где m - масса идеального газа а тепловой машине. Количество отдаваемого холодильнику тепла Q2 равно работе А34, затрачиваемой на сжатие газа при переводе его из состояния 3 в состояние 4. Эта работа равна:
Для того, чтобы цикл был замкнутым, нужно, чтобы состояния 4 и 1 лежали на одной и той же адиабате. Отсюда с помощью (2.1.68) можно получить:
Аналогично, поскольку состояния 2 и 3 лежат на одной и той же адиабате, выполняется:
Деля (2.3.11) на (2.3.10), приходим к условию замкнутости цикла:
Подставляя (2.3.8) и (2.3.9) в (2.3.6), имеем:
Окончательно, учитывая условие (2.3.12), для КПД тепловой машины, работающей по циклу Карно для идеального газа, получаем:
Следовательно, КПД цикла Карно для идеального газа оказывается зависящим только от температуры нагревателя и холодильника. Даже для наилучшей тепловой машины, работающей по циклу Карно, КПД всегда значительно меньше единицы. Если, например, температура нагревателя Т1 = 373К (температура кипения воды), а температура холодильника Т2 = 293К (комнатная температура), то η = 22%. И этот КПД является верхним (и недостижимым) пределом. В реальных машинах, например, на паровозах, редко превосходил 10%. 2.3.6. ЭнтропияОбратим внимание на те изменения, которые претерпело рабочее тело в процессе кругового цикла Карно. Из исходного состояния 1 (давление р1, температура Т1) рабочее тело путем последовательного проведения изотермического и адиабатического расширений перешло в состояние 3, когда оно приняло температуру холодильника Т2. Это изменение состояния произошло за счет тепла Q1, доставленного рабочему телу нагревателем. Обратный переход рабочего тела из состояния 3 в исходное состояние 1 был осуществлен двумя последовательно проведенными изотермическим и адиабатическим сжатиями тела. Выделившееся при этом возвращении в исходное состояние количество тепла равно Q2, причем Q2 < Q1. Таким образом, оказывается, что обратимый переход одного и того же тела из состояния 1 → 3 и обратный переход 3 → 1 сопровождаются неодинаковыми количествами поглощенного и выделенного тепла. Очевидно, что это связано с тем, что оба перехода были проведены различными путями: в одном случае (1 → 3) процесс расширения происходил при давлении более высоком, чем процессы сжатия в другом (3 → 1). Ясно, что если бы мы осуществили переход 3 → 1 тем же путем, что и прямой, т.е. по кривой 3 → 2 → 1, а не по кривой 3 → 4 → 1 (Рис. 2.3.4), то количество тепла, затраченного при прямом переходе, в точности равнялось бы количеству тепла, выделившемуся при обратном переходе. Отсюда следует важный вывод: количество тепла, которое должно быть доставлено телу или отнято у него при переходе из одного состояния в другое, не определяется однозначно начальным и конечным состояниями, но существенно зависит от способа осуществления этого перехода. Однако, хотя сами количества тепла - Q1, доставленного рабочему телу нагревателем при температуре Т1, и Q2, переданное рабочим телом холодильнику при температуре Т2, не равны между собой, то, как следует из сопоставления формул (2.3.8), (2.3.9) и (2.3.12), отношения этих теплот к тем температурам, при которых они были поглощены или отданы, численно равны между собой (но имеют противоположные знаки):
Отношение Обобщим данный результат. Любое изменение состояния тела или системы тел в общем случае можно представить как результат бесконечно большого числа бесконечно малых изменений. При каждом таком бесконечно малом изменении система либо поглощает, либо выделяет бесконечно малое количество тепла dQ (если процесс не адиабатический). Пусть dQ > 0, когда система поглощает тепло. Можно показать, что если система в результате каких-либо изменений состояния переходит обратимым путем из состояния А в состояние В, то сумма приведенных количеств теплоты
Докажем сначала, что при любом круговом процессе интеграл (2.3.16) не может быть положительным. Пусть некоторое тело М совершает круговой процесс. Во время процесса тело отдавало и поглощало тепло. Пусть тепло, выделяемое телом М, передается тепловому резервуару с температурой Т1. Используя (2.3.15), можно записать:
где dQ - количество тепла, отнятое от тела М при температуре Т, dQ' - количество тепла, переданное резервуару с температурой Т1. Если Т1 < T, резервуар играет роль холодильника, а тело М - нагревателя, и наоборот. После того, как телом М будет завершен круговой процесс, общее количествo теплоты, потерянное телом, как следует из (2.3.17), должно быть равно величине Процесс, совершенный телом, - круговой. Поэтому оно в конце концов не испытало никаких изменений. Если бы интеграл (2.3.16) оказался положительным, то это означало бы, что потерянное телом количество тепла
Отсюда следует, что для обратимого процесса интеграл
Энтропия - аддитивная величина. Это означает, что энтропия системы равна сумме энтропий отдельных ее частей. Изменение энтропии системы, которой сообщено бесконечно малое количество тепла dQ, определяется соотношением:
Тогда первое начало термодинамики можно записать так:
Энтропия изолированной системы может только возрастать (если в системе протекает необратимый процесс), или оставаться постоянной в случае обратимого процесса. Нернстом доказана теорема (иногда называемая третьим началом термодинамики), согласно которой при стремлении абсолютной температуры к нулю энтропия любого тела также стремится к нулю:
Тогда энтропию состояния тела при температуре Т можно вычислить так:
|
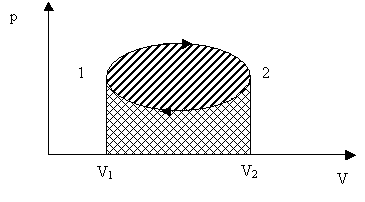
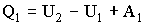
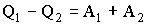
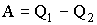
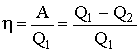
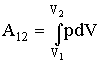
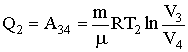
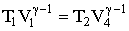
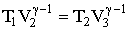
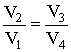
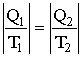
называют, следуя Лоренцу, приведенной теплотой. Из (2.3.15) следует, что приведенные теплоты, полученные и отданные рабочим телом при круговом процессе, равны между собой.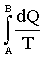
не зависит от пути, по которому происходил этот переход. Это означает, что интеграл по замкнутому контуру должен быть равен нулю: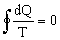
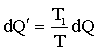
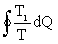. Поскольку теплоемкость резервуара велика и его температура остается постоянной, эта величина будет равна: 
.
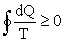, несостоятельно. Аналогично можно показать, что указанный интеграл не может быть отрицательным. Но если он не может быть ни положительным, ни отрицательным, то это означает, что для обратимых круговых процессов выполняется:
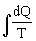не зависит от пути, по которому проходит процесс, и зависит только от начального и конечного положений. Поэтому вводят новую величину, которая называется энтропией:
