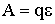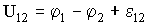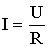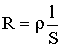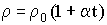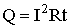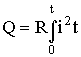ТЕМА 3.5. Постоянный электрический ток
3.5.1. Электрический ток
3.5.2. Электродвижущая сила
3.5.3. Закон Ома. Сопротивление проводников
3.5.4. Закон Джоуля-Ленца
3.5.5. Правила Кирхгофа для разветвленных цепей
3.5.1. Электрический ток
Если в проводнике создать электрическое поле, то носители заряда придут в упорядоченное движение: положительные заряды будут двигаться в направлении поля, отрицательные - в противоположном направлении. Электрический ток возможен в твердых телах - металлах, где носителями тока служат электроны, в жидкостях и газах, где в качестве носителей тока могут выступать положительные и отрицательные ионы и электроны. Упорядоченное движение электрических зарядов называется электрическим током. Ток характеризуют с помощью силы тока - скалярной величины, численно равной заряду, переносимому через рассматриваемую поверхность в единицу времени:
Если в проводнике движутся носители заряда обоих знаков, то имеем:
За направление электрического тока принято направление движения положительных зарядов. Носители заряда испытывают взаимодействие со средой, в которой они распространяются, и, как и свободные молекулы и атомы, под действием температуры в отсутствие поля движутся хаотически с некоторой скоростью
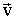 .
Среднее значение этой скорости будет равно нулю. При включении поля на хаотическое движение со скоростью .
Среднее значение этой скорости будет равно нулю. При включении поля на хаотическое движение со скоростью
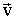 налагается упорядоченное движение со скоростью налагается упорядоченное движение со скоростью
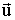 , благодаря чему и возникает электрический ток. , благодаря чему и возникает электрический ток.
Для анализа распределения тока в проводниках применяют также вектор плотности тока:
где dS - площадка, перпендикулярная движению зарядов dq.
Пусть в единице объема содержится n+ положительных и n- отрицательных носителей зарядов. Абсолютная величина этих зарядов равна соответственно e+ и e-. Если под действием поля носители приобретают скорости u+ и u-, то за единицу времени через площадку единичной площади пройдет n+u+ положительных зарядов. Тогда для полной плотности тока получим:
Ток, не изменяющийся со временем, называется постоянным. Очевидно, что выполняется:
В системе СИ за единицу тока принимают 1 А.
3.5.2. Электродвижущая сила
Если в проводнике создать электрическое поле и не принять мер к его поддержанию, то перемещение зарядов быстро приведет к тому, что поле внутри проводника исчезнет и ток прекратится. Для того чтобы поддерживать ток длительное время, нужно от конца проводника с меньшим потенциалом (считаем, что носители тока имеют положительный заряд) непрерывно отводить приносимые сюда заряды, а к концу с большим потенциалом непрерывно их доставлять (Рис. 3.5.1).

Рис. 3.5.1. Циркуляция зарядов
Иначе говоря, надо осуществить циркуляцию зарядов по замкнутому пути. Однако циркуляция вектора электростатического поля на замкнутом пути равна нулю. Поэтому в замкнутой цепи наряду с участками, на которых положительные заряды движутся в сторону убывания потенциала, должны быть участки, где эти же заряды движутся в противоположном направлении (в сторону возрастания потенциала), т.е. против сил электростатического поля. Перемещение зарядов на таких участков можно совершить только за счет сил неэлектростатической природы, называемых сторонними силами. Следовательно, для поддержания тока необходимы сторонние силы, которые могут быть, например, обусловлены химическими процессами в аккумуляторах.
Сторонние силы характеризуют работой, которую они совершают над перемещающимися по цепи зарядами. Величина, равная работе сторонних сил, отнесенной к величине положительного заряда, называется электродвижущей силой (ЭДС), действующей в цепи или на ее участке:
Размерность этой величины совпадает с размерностью потенциала.
Стороннюю силу, действующую на заряд q, представим в виде:
где 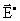 - напряженность поля сторонних сил. - напряженность поля сторонних сил.
Работу сторонних сил на всем протяжении замкнутой цепи можно выразить так:
Используя (3.5.6) и (3.5.8), получим ЭДС:
Кроме сторонних сил, на заряд действуют силы электростатического поля 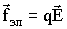 . Следовательно, результирующая сила, действующая в каждой точке цепи на заряд q, равна: . Следовательно, результирующая сила, действующая в каждой точке цепи на заряд q, равна:
Работа, совершаемая этими силами на некотором участке 1-2, имеет вид:
Для замкнутой цепи работа электростатических сил равна нулю, поэтому выполняется:
Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения (напряжением) U на данном участке цепи. Из (3.5.11) следует:
При отсутствии сторонних сил напряжение совпадает с разностью потенциалов.
3.5.3. Закон Ома.
Сопротивление проводников
Георг Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения на проводнике:
Выражение (3.5.14) справедливо для участка цепи, на котором не действуют сторонние силы. В этом случае напряжение совпадает с разностью потенциалов на концах проводника. Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит 1 Ом, равный сопротивлению такого проводника, по которому течет ток в 1 А при напряжении в 1 В.
Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он изготовлен. Для однородного цилиндрического проводника выполняется:
где l - длина проводника, S - площадь его поперечного сечения, ρ - удельное электрическое сопротивление материала (размерность последнего 1 Ом·м).
Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону:
где ρ0 - удельное сопротивление при 0°С.
При низких температурах наблюдается отклонение от закона (3.5.16) (Рис. 3.5.2).
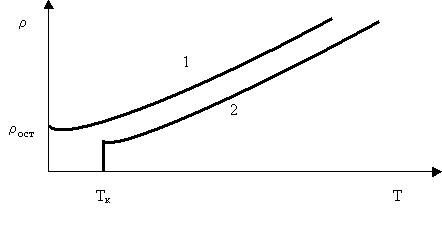
Рис. 3.5.2. Зависимость сопротивления металлов от температуры
В большинстве металлов зависимость ρ(Т) следует кривой 1. Величина остаточного сопротивления в сильной степени зависит от чистоты материала и наличия механических напряжений в образцах.
Зависимость электрического сопротивления от температуры положена в основу действия термометров сопротивления, представляющих собой платиновую проволоку, намотанную на фарфоровый каркас. После градуировки такой термометр позволяет измерять температуру в широком интервале температур.
У большой группы металлов и сплавов при температурах порядка нескольких градусов Кельвина сопротивление скачком обращается в нуль (кривая 2). Это - явление сверхпроводимости. Ток в сверхпроводящем кольце будет циркулировать даже в отсутствие электрического поля годами. Для каждого проводника имеется своя критическая температура Тк, при которой он становится сверхпроводником. При действии на сверхпроводник магнитного поля определенного значения сверхпроводимость разрушается.
В 1986 г. были открыты высокотемпературные сверхпроводники с Тк = 94К.
3.5.4. Закон Джоуля-Ленца
Ток, проходящий через проводник, нагревает последний. Дж. Джоуль и, независимо от него, Э. Ленц установили экспериментально, что количество выделяющегося в проводнике тепла определяется соотношением:
где t - время протекания тока.
Если сила тока изменяется со временем, имеем:
Нагревание проводника происходит за счет работы, совершаемой силами поля над носителями заряда и обусловленной электрическим сопротивлением проводника.
3.5.5. Правила Кирхгофа
для разветвленных цепей
Расчет разветвленных цепей упрощается, если применять правила Кирхгофа. Первое относится к узлам цепи. Узел - это точка, в которой сходится более чем два проводника (Рис. 3.5.3).

Рис. 3.5.3. Пример узла цепи
Ток, текущий к узлу, считается имеющим один знак ("плюс" или "минус"), текущий от узла имеет противоположный знак ("минус" или "плюс").
Первое правило Кирхгофа гласит: алгебраическая сумма токов, сходящихся в узле, равна нулю:
Если бы алгебраическая сумма токов отличалась от нуля, в узле происходило бы накопление или уменьшение заряда, что в свою очередь привело бы к изменению потенциала узла и к изменению текущих через узел токов. Поэтому условие (3.5.19) эквивалентно требованию постоянства токов. Уравнение вида (3.5.19) можно записать для каждого из N узлов цепи, однако независимыми будут только (N - 1) уравнение.
Выделим мысленно в разветвленной цепи произвольный замкнутый контур 1 - 2 - 3 - 4 - 1 (Рис. 3.5.4).
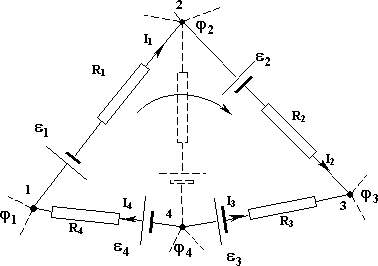
Рис. 3.5.4. К выводу второго правила Кирхгофа
Зададимся направлением обхода (например, по часовой стрелке) и применим к каждому из неразветвленных участков контура закон Ома:
При сложении этих выражений потенциалы сокращаются, и получается уравнение (второе правило Кирхгофа): в замкнутом контуре разветвленной цепи алгебраическая сумма электродвижущих сил источников тока равна алгебраической сумме произведений сил тока на сопротивления соответствующих участков этого контура
| 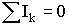

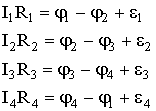

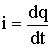
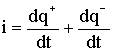
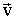 .
Среднее значение этой скорости будет равно нулю. При включении поля на хаотическое движение со скоростью
.
Среднее значение этой скорости будет равно нулю. При включении поля на хаотическое движение со скоростью
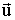 , благодаря чему и возникает электрический ток.
, благодаря чему и возникает электрический ток.
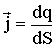
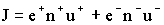
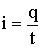

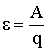

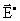 - напряженность поля сторонних сил.
- напряженность поля сторонних сил.

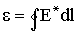
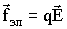 . Следовательно, результирующая сила, действующая в каждой точке цепи на заряд q, равна:
. Следовательно, результирующая сила, действующая в каждой точке цепи на заряд q, равна: