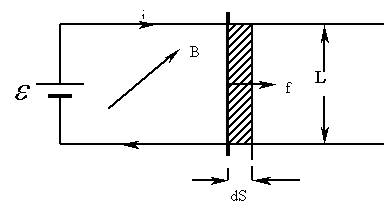
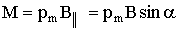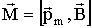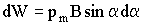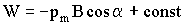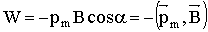где i - сила тока, Величина силы вычисляется по формуле:
где α - угол между векторами
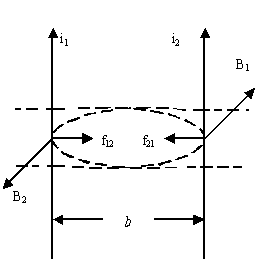
Направление силы определяют в соответствии с векторным произведением либо используя правило левой руки: если расположить левую руку так, чтобы вектор магнитной индукции входил бы в ладонь, а четыре сложенных пальца были направлены вдоль тока, то отогнутый большой палец покажет направление действия силы. Применим закон Ампера для вычисления силы взаимодействия между двумя находящимися в вакууме бесконечными прямолинейными проводниками. Если расстояние между токами равно b (Рис. 3.7.2), то каждый элемент тока i2 будет находиться в магнитном поле с индукцией
Угол между элементом тока и вектором магнитной индукции - прямой. Тогда, с помощью (3.7.2), имеем:
Выражение (3.7.3) совпадает с ранее введенным (3.6.1). Для силы f12, действующей на единицу длины тока i1, получается аналогичное соотношение. С помощью правила левой руки легко установить, что при одинаковом направлении токов они притягивают друг друга и отталкиваются при противоположном направлении. 3.7.2. Сила ЛоренцаПроводник, по которому течет ток, отличается от проводника без тока только тем, что в нем происходит упорядоченное движение зарядов. Отсюда следует, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, и от них передается проводнику. Используя закон Ампера (3.7.1) и заменяя в нем
где dV - элементарный объем проводника, к которому приложена сила. Для объемной плотности этой силы имеем:
Используя выражение для плотности тока, (3.7.5) можно переписать так:
Эта сила равна сумме сил, приложенным к носителям, заключенным в объеме dV. Таких носителей -n, следовательно, но один носитель с зарядом q, движущийся со скоростью
Эту силу и называют силой Лоренца. Ее модуль равен:
где α - угол между векторами Сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы
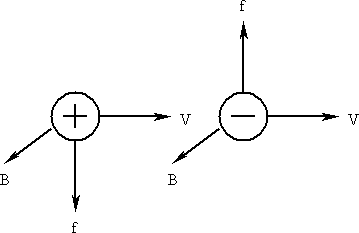
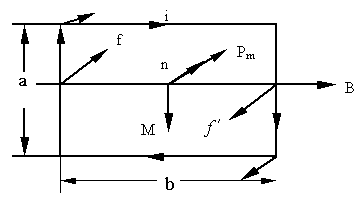
Поскольку сила Лоренца всегда направлена перпендикулярно скорости заряженной частицы, она не совершает работы над частицей. Следовательно, действуя на заряженную частицу постоянным магнитным полем, нельзя изменить ее энергию. 3.7.3. Контур с током в магнитном полеПусть прямоугольный плоский контур с током помещается в однородном магнитном поле. Если контур ориентирован так, что вектор магнитной индукции параллелен его плоскости (Рис. 3.7.4), то стороны, имеющие длину b, не будут испытывать действие силы Ампера, так как для этих сторон sinα = 0.
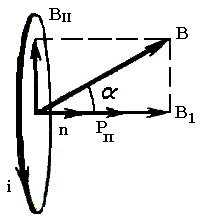
На левый участок, согласно закону Ампера, будет действовать сила f = iBa, направленная за чертеж, на правый участок - такая же по величине, но противоположно направленная сила f'. Эти силы образуют пару сил, момент которой равен:
Учитывая, что ab = S (площади контура), а произведение iS = pm, соотношение (3.7.9) можно представить так:
что совпадает с определением (3.6.3). Вращающий момент
В этом случае выполняется:
Направления всех сил (3.7.11) лежат в плоскости контура. Вращательный момент в этом случае не возникает. Равнодействующая всех сил равна нулю; силы лишь растягивают контур, не перемещая и не поворачивая его в пространстве. Если повернуть контур на 180° или изменить направление магнитного поля на противоположное, то направления всех сил изменятся на противоположные, и они будут сжимать контур. При произвольной ориентации контура относительно вектора
Составляющая
Принимая во внимание взаимную ориентацию векторов
Для того, чтобы угол α между векторами
Поворачиваясь в первоначальное положение, контур может возвратить затраченную на его поворот работу, совершив ее над какими-либо телами. Следовательно, работа (3.7.14) идет на увеличение энергии W, которую получает контур с током в магнитном поле:
Интегрируя (3.7.15), можно получить:
Полагая const = 0, получаем формулу для энергии контура с током в магнитном поле:
Вообще, поворот контура с током в магнитном поле положен в основу действия электрических двигателей. 3.7.4. Работа, совершаемая при перемещении
|
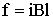 | (3.7.18) |
где l - длина перемещающегося участка тока.
На пути ds эта сила совершит над проводником работу:
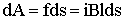 | (3.7.19) |
Произведение lds равно заштрихованной площади (Рис. 3.7.7), а Blds = ВdS = dΦ - потоку магнитной индукции через эту площадку. Поэтому можно получить соотношение:
Рассмотрим магнитное поле в соленоиде. Соленоидом называют катушку цилиндрической формы из провода, витки которого намотаны в одном направлении (Рис. 3.7.8).
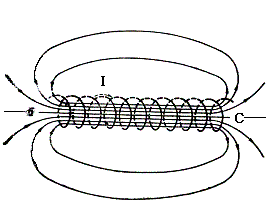
Рис. 3.7.8. Магнитное поле в соленоиде
Магнитное поле соленоида представляет собой результат сложения полей, создаваемых несколькими круговыми токами, расположенными рядом и имеющими общую ось. Внутри соленоида линии индукции каждого витка складываются, тогда как между соседними витками они имеют противоположное направление. Поэтому при достаточно плотной намотке соленоида одинаково направленные поля сольются в общую замкнутую линию, проходящую внутри соленоида и охватывающую его снаружи. Внутри длинного соленоида магнитное поле оказывается практически однородным, вне соленоида - сравнительно слабым. Если соленоид имеет (гипотетически) бесконечную длину, то магнитное поле сосредоточено полностью внутри соленоида.
Пусть соленоид (Рис. 3.7.9) имеет длину l, радиус его витков равен R, число витков составляет N, сила тока равна I.
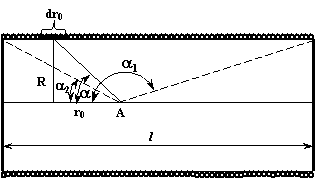
Рис. 3.7.9. К расчету магнитного поля в соленоиде
Рассматривая соленоид как совокупность вплотную прилегающих витков (круговых токов I), имеющих общую ось, определим индукцию магнитного поля В в точке А на оси соленоида как сумму индукций каждого из витков. Воспользуемся формулой (3.6.14), которую сейчас следует записать так:
 | (3.7.20) |
Выделим участок соленоида длиной dr0. В нем содержится Ndr0/l витков. Тогда индукция поля от одного витка равна:
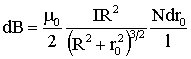 | (3.7.21) |
Из Рис. 3.7.9 видно, что r0 = Rctgα. Тогда
R2 + r02 = R·(1 + ctg2α) = R/sin2α.
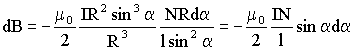 | (3.7.22) |
Интегрируя (3.7.22) в пределах от α = α1 до α = α2, найдем полную индукцию:
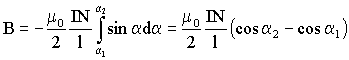 | (3.7.23) |
Для бесконечно длинного соленоида выполняется α1 = 0° и α2 = 180°. Поэтому получим:
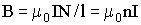 | (3.7.24) |
где n = N/l - число витков на единицу длины соленоида.
Если соленоид заполнен магнитным материалом с магнитной проницаемостью μ, то (3.7.23) должно быть записано так:
 | (3.7.25) |
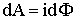 | (3.7.26) |
Отметим, что работа совершается не за счет магнитного поля (сила Лоренца работы над движущимися зарядами не совершает), а за счет источника, поддерживающего ток в контуре.
|
|
 в магнитном поле действует сила:
в магнитном поле действует сила:
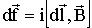
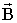 - магнитная индукция в том месте, где находится элемент тока
- магнитная индукция в том месте, где находится элемент тока 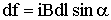

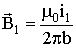 .
.
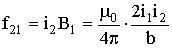
 , это соотношением можно представить так:
, это соотношением можно представить так:
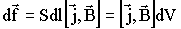
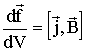
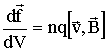
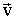 в магнитном поле
в магнитном поле 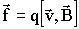


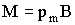
 стремится повернуть контур так, чтобы его магнитный момент
стремится повернуть контур так, чтобы его магнитный момент 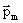 установился по направлению вектора
установился по направлению вектора 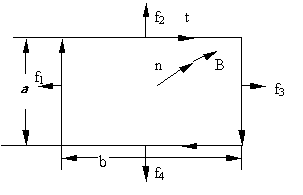

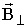 - перпендикулярную и
- перпендикулярную и 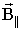 - параллельную плоскости контура, и рассматривать действие каждой составляющей раздельно (Рис. 3.7.6).
- параллельную плоскости контура, и рассматривать действие каждой составляющей раздельно (Рис. 3.7.6).