Лабораторная работа № 7.
Исследование затухающих механических
колебаний с помощью самописца
Цель работы: ознакомиться с принципом работы самописца; на примере механических колебаний научиться регистрировать динамические процессы и использовать диаграмму для определения их параметров; определить основные параметры (период, частоту, логарифмический декремент затухания, коэффициент затухания) механических колебаний.
Литература: §§ 140, 141, 146.
Приборы и материалы: самописец, маятник с потенциометрическим датчиком, набор грузов, линейка.
Колебаниями называются повторяющиеся во времени движения или изменения состояния исследуемого объекта. Гармоническими называют колебания, при которых исследуемая величина изменяется во времени по закону синуса или косинуса:
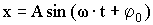
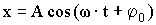 | (1.1) |
где х - исследуемая величина при механических колебаниях (смещение маятника от положения равновесия); А - амплитуда х; ω - круговая или циклическая частота (ω=2πν) - число колебаний за 2π секунд; t - время; φ0 - начальная фаза колебания; период (Т) - время, за которое совершается одно полное колебание; частота (ν) - число колебаний за единицу времени ν=1/Т.
Рассмотрим колебания математического маятника. Математическим маятником называют материальную точку, подвешенную на тонкой, нерастяжимой и невесомой нити. Моделью математического маятника может служить груз, подвешенный на тонкой упругой нити длиной l. Когда маятник находится в положении равновесия сила тяжести груза уравновешена натяжением нити. При отклонении груза сила тяжести и сила натяжения нити действуют на груз под углом друг к другу. Равнодействующая этих двух сил всегда будет направлена к положению равновесия, причем величина ее будет тем больше, чем больше отклонен маятник от положения равновесия. Величина силы F , возвращающей маятник к положению равновесия, зависит от угла отклонения маятника φ. Колебания такого маятника описываются дифференциальным уравнением второго порядка:  Это выражение является дифференциальным уравнением незатухающих гармонических колебаний, его решением служат уравнения (1.1). Это выражение является дифференциальным уравнением незатухающих гармонических колебаний, его решением служат уравнения (1.1).
В реальных условиях движение тел всегда сопровождается трением, часть энергии тела расходуется на совершение работы против сил трения и колебания затухают. Величина силы трения зависит от свойств (r) вещества, в котором происходит движение тела (вода, воздух), и от скорости движения тела (v) (сила трения увеличивается с ростом скорости и направлена противоположно ей). Пусть сила трения пропорциональна величине скорости:
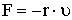 | (1.2) |
В этом случае дифференциальное уравнение затухающих колебаний имеет вид:
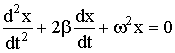 | (1.3) |
Решение этого уравнения показывает, что амплитуда затухающих колебаниях убывает по экспоненциальному закону:
 | (1.4) |
где Аt - амплитуда колебания в момент t; А0 - начальная амплитуда колебания; е - основание натурального логарифма; t - время колебания; β - показатель затухания, который зависит от массы тела и величины силы трения β = r/2m.
Решение дифференциального уравнения затухающих колебаний:
 | (1.5) |
Одной из характеристик затухающих колебаний является логарифмический декремент затухания - λ. Он определяется как натуральный логарифм отношения амплитуд, соответствующих моментам времени, отличающимся на период, и характеризует скорость убывания амплитуды:
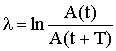 | (1.6) |

Порядок выполнения работы
- Включите самописец и потенциометрический датчик.
- Подвесьте на нить маятника груз массой 100г, отклоните маятник от положения равновесия на 15-20 см и отпустите его. Зарегистрируйте на ленте самописца 10-15 колебаний. Как на рисунке.
- Измените вес тела маятника (200 г) и повторите регистрацию колебаний.
- Скорость движения каретки самописца посмотрите на панели самописца (v). По диаграмме измерьте смещения (Z), соответствующие разному числу колебаний (n) (на рисунке приведены примеры определения Z для n=3 и 7), для пяти разных n. Определите период (Т) и частоту (v) колебаний по формулам:
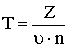 ; ; 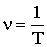
- Для каждой пары двух рядом расположенных колебаний измерьте амплитуды А(t) и А(t+Т) (на рисунке приведены примеры определения амплитуд второго и третьего колебаний). Определите логарифмический декремент затухания по формуле (1.6). Повторите такие замеры для пяти аналогичных пар отклонений. Определите для каждой пары колебаний значение логарифмического декремента затухания, рассчитайте среднее значение λср, среднюю квадратичную ошибку определения (Δλср).
По средним значениям рассчитайте показатель затухания : β = λср/Тср.
Таблица 1
| № | Z | n | T | v | A(t) | A(t+T) | λ | λср | Δλср | β |
|---|
| Ед. изм. | м | | с | Гц | мм | мм | | | | |
| 1 | | | | | | | | | | |
Контрольные вопросы
- Выведите дифференциальное уравнение гармонических колебаний.
- Докажите, что уравнение
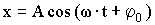 является решением дифференциального уравнения гармонических колебаний. является решением дифференциального уравнения гармонических колебаний.
- Укажите графический смысл амплитуды, фазы и других характеристик гармонического колебания.
- Как изменяется амплитуда колебаний при наличии трения?
- Выведите дифференциальное уравнение затухающих колебаний.
- Как определить показатель затухания? Логарифмический декремент затухания? Напишите формулы.
- С помощью математических преобразований покажите связь логарифмического декремента затухания и показателя затухания.
| 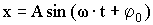
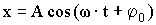
 Это выражение является дифференциальным уравнением незатухающих гармонических колебаний, его решением служат уравнения (1.1).
Это выражение является дифференциальным уравнением незатухающих гармонических колебаний, его решением служат уравнения (1.1).
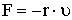
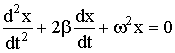


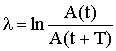

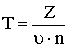 ;
; 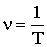
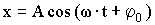 является решением дифференциального уравнения гармонических колебаний.
является решением дифференциального уравнения гармонических колебаний.