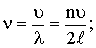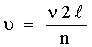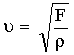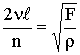Лабораторная работа № 8.
Изучение стоячей волны в вертикальной струне
Цель работы: наблюдать стоячую волну в струне, ознакомиться с методом определения линейной плотности струны с помощью стоячей волны.
Литература: §§ 153-157.
Приборы и материалы: генератор звуковой частоты, штатив, рулетка, грузы, вибратор.
Колебание, возникнув в какой-либо точке среды, не остается в этой точке, а распространяется по всей среде (благодаря наличию упругих связей между частицами среды). Процесс распространения колебаний в среде называется волной. Пусть в однородной среде без потерь распространяется вдоль оси x плоская волна, излучаемая гармоническим вибратором, который находится в точке О. Закон колебаний вибратора y=A sin ωt, где у - смещение точки в момент времени t. Закон колебаний любой точки среды с координатой x можно записать в виде: y=A sin ω[t-τ], где у - смещение точки с координатой x в момент времени t, τ - время запаздывания, т.е. время, которое необходимо, чтобы возмущение от точки О дошло до точки с координатой x. Если v - скорость распространения возмущения (фазовая скорость), то τ = х/v. Поэтому 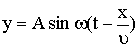 - уравнение бегущей волны. Уравнение волны может быть представлено и в таком виде: - уравнение бегущей волны. Уравнение волны может быть представлено и в таком виде:

где λ - длина волны.
При выводе уравнения бегущей волны мы описывали волновой процесс в бесконечной среде, в которой волны идут вдоль оси x, не отражаясь. В реальных условиях, дойдя до границы двух сред, волна отражается. Следовательно, будет наблюдаться процесс наложения прямой (бегущей) и обратной (отраженной) волн. Если среда ограничена с двух сторон, то в результате многократных отражений может возникнуть стоячая волна. Стоячей волной называется устойчивый результат наложения бегущей и отраженной волн.
Запишем уравнения двух встречных волн:
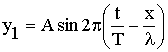 |
(бегущая волна) |
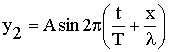 |
(отраженная волна) |
Сложив эти уравнения, получим смещение в стоячей волне:
где 2Acos(2πx/λ) - амплитуда стоячей волны.
Легко видеть, что точки в стоячей волне колеблются с различными амплитудами. Точки, смещения которых всегда равны нулю, называются узлами стоячей волны и удовлетворяют условию:
Точки, амплитуды колебаний которых максимальны, называются пучностями стоячей волны и удовлетворяют условию:
где х - координаты узлов и пучностей соответственно. Расстояние между узлом и пучностью λ/4, а расстояние между соседними пучностями λ/2.
Установка для наблюдения стоячей волны состоит из постоянного магнита, между полюсами которого расположена катушка с сердечником, и звукового генератора (ЗГ). При пропускании тока звуковой частоты по обмотке катушки, в результате взаимодействия магнитных полей катушки и постоянного магнита, сердечник совершает колебания, соответствующие колебаниям тока в катушке. Стоячие волны наблюдаются на вертикальной струне, один конец которой соединен с сердечником катушки, а на другой подвешен груз массой m.

Периодическая, вынуждающая сила создается полем катушки. При совпадении частоты генератора с одной из собственных частот струны в ней устанавливается стоячая волна. Так как концы струны закреплены, на концах ее образуются узлы. При резонансе на длине струны укладывается целое число полуволн:  , где n - число полуволн (пучностей), λ - длина бегущей волны. Длина волны связана со скоростью распространения деформации вдоль струны и с частотой колебаний соотношением: , где n - число полуволн (пучностей), λ - длина бегущей волны. Длина волны связана со скоростью распространения деформации вдоль струны и с частотой колебаний соотношением:
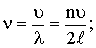
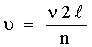 |
(1.1) |
Скорость распространения деформации вдоль струны:
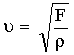 |
(1.2) |
где F = mg - сила натяжения; ρ - линейная плотность материала струны.
Подставив в выражение (1.2) значения из формулы (1.1), получим:
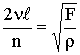 |
(1.3) |
откуда
 |
(1.4) |
Порядок выполнения работы
- Измерьте рулеткой длину струны.
- Включите ЗГ и, меняя частоту тока катушки в пределах от 0 до 90 Гц, найдите частоты, при которых на струне устанавливаются стоячие волны с числом пучностей n=2, 3, 4, 5, 6.
- Для каждого случая установившейся стоячей волны на струне определите частоту n и число пучностей n на струне. Вычислите линейную плотность материала струны (ρ) по формуле 1.4. Данные занесите в таблицу.
Таблица 1
| № |
l |
m |
n |
v |
ρ |
ρср |
+Δρср |
| Ед. изм. | | | | | | | |
| 1 | | | | | | | |
Контрольные вопросы
- Запишите уравнение бегущей волны.
- Какая волна называется стоячей?
- Запишите уравнение, описывающее смещение в стоячей волне.
- Что такое пучность и узел стоячей волны?
- Чем стоячая волна отличается от бегущей?
| 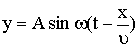 - уравнение бегущей волны. Уравнение волны может быть представлено и в таком виде:
- уравнение бегущей волны. Уравнение волны может быть представлено и в таком виде:

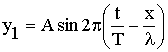
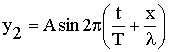
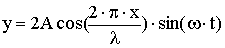
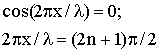
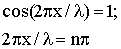

 , где n - число полуволн (пучностей), λ - длина бегущей волны. Длина волны связана со скоростью распространения деформации вдоль струны и с частотой колебаний соотношением:
, где n - число полуволн (пучностей), λ - длина бегущей волны. Длина волны связана со скоростью распространения деформации вдоль струны и с частотой колебаний соотношением: