Лабораторная работа № 10.
Определение отношения удельных теплоемкостей газов
Цель работы: изучение адиабатического процесса и методов определения отношения Ср к Сv.
Литература: §§ 50-55
Приборы и материалы: стеклянный баллон, насос, манометр, секундомер.
Величина отношения удельной теплоемкости при постоянном давлении Ср к удельной теплоемкости при постоянном объеме Сv: γ = Cp/Cv для газов играет очень большую роль при адиабатических процессах, близких к ним. Для примера укажем, что ею, в частности, определяется скорость распространения звука в газах, от нее зависит течение газов по трубам со звуковыми скоростями и достижение сверхзвуковых скоростей в расширяющихся трубах.
.gif)
Экспериментальная установка (рис.1) состоит из стеклянного баллона объемом V0, который сообщается с насосом U - образным манометром М, заполненным водой. Кран К служит для сообщения баллона с атмосферой. В баллоне находится некоторое количество воздуха. Пусть первоначально в нем было атмосферное давление Р0. Если при помощи насоса накачать в баллон небольшое количество воздуха, то прежний газ в баллоне окажется несколько сжатым, его объем уменьшится и станет V1, причем V1 < V0, а давление газа повысится, о чем можно судить по разности уровней жидкости в манометре. Но, так как сжатие воздуха в баллоне произведено очень быстро и тепловой обмен с окружающей средой почти не произошло (адиабатическое сжатие), то температура воздуха внутри немного повысится. Поэтому окончательная разность уровней Н в манометре установится только тогда, когда температура воздуха внутри баллона сравняется с температурой комнаты, благодаря теплопроводности стенок баллона. Обозначим через Т1 абсолютную температуру комнаты, через Р1 - давление газа внутри баллона. Тогда Р1 = Р0 + H Следовательно, 1-е состояние газа характеризуется параметрами Р1; V1; T1. Если теперь быстро открыть кран К, то воздух в баллоне будет расширяться и займет объем всего баллона V0. А так как процесс расширения в баллоне протекает очень быстро (почти адиаба тически), то газ охладится до температуры Т2 ниже комнатной: Т2 > T1. Давление в баллоне станет равным тмосферному давлению Р0. Это мы заметим по манометру, так как в этот момент уровни жидкости в манометре сравняются.
.gif)
В этот момент кран К закрывают. Следовательно, 2-е состояние газа характеризуется параметрами Р0; V0; T2.
Второе состояние газа очень непродолжительно. Охладившийся воздух в баллоне будет нагреваться, пока его температура не сравняется с температурой окружающей среды, приняв вновь значение Т1. Вследствие этого давление в баллоне возрастает до величины Р2, которое больше атмосферного давления на отсчитанную по манометру разность h, т.е. Р2 = Р0 + h. Объем воздуха можно считать тем же, что и во втором состоянии, т.е. V0, так как расширение воздуха будет очень незначительным. Следовательно, 3-е состояние газа характеризуется параметрами Р2; V0; T1. Переход из второго состояния в третье произошел изохорически. Для 1 и 3 состояний можно записать 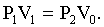 Для 1 и 2 состояний справедливо уравнение Пуассона Для 1 и 2 состояний справедливо уравнение Пуассона 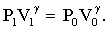
Решая совместно эту систему уравнений относительно искомой величины γ, получим формулу для расчета этой величины: 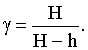 Следовательно, для определения γ необходимо знать избыточное (над атмосферным) давление в баллоне до адиабатического расширения газа (Н) и его избыточное давление после изохорического нагревания (h). Следовательно, для определения γ необходимо знать избыточное (над атмосферным) давление в баллоне до адиабатического расширения газа (Н) и его избыточное давление после изохорического нагревания (h).
Наиболее сложной частью данной работы является определение величины h. Дело в том, что практически невозможно осуществить совпадение момента перекрытия крана К с моментом окончания процесса адиабатического расширения, когда давление в баллоне станет атмосферным Р0. Если кран закрыть раньше, чем давление упадет до атмосферного, то получим завышенное значение h1, и, наоборот, при запаздывании получается заниженное значение h11. Как показывает опыт, между значением h, заниженным значение h11 и временем существует связь lgh11 = lgh - kt (k = соnst). На рис.2 представлен график зависимости lgh11 и t, из которого видно, что, повторив опыт несколько раз (от одной и той же величины Н) с различным временем запаздывания и, построив график в координатах lgh11 и t, можно путем экстраполяции определить lgh, а, следовательно, и h.
Указания к выполнению работы
- Для определения Н накачиваем в баллон воздух до тех пор, пока разность уровней в манометре не будет равна 200-250 мм, и перекрываем кран В. Через 2-3 мин., когда давление в баллоне перестанет изменяться, отсчитываем показание манометра. Отсчет следует делать по нижнему краю мениска.
- Для определения h открываем кран К, одновременно включаем секундомер и держим кран открытым 5 с., затем кран К перекрываем. Через примерно 3 мин. отсчитываем показание манометра h11. Опыт повторяем со временем запаздывания 9, 13, 17, 21, 25 секунд. При этом необходимо следить за тем, чтобы Н во всех опытах было одно и тоже.
По полученным данным строим график зависимости lgh11 от t, из которого определяем h (рис.2)
- Опыт проводим при трех различных значениях Н.
- Оцениваем точность эксперимента путем подсчета средней квадратичной погрешности с надежностью α = 0,9.
- Результаты измерений заносим в таблицы.
- В отчете представить полный расчет величин.
Таблица 1
| H(мм.H20) | t(c) | 5c. | 9c. | 13c. | 17c. | 21c. | 25c. |
|---|
| H1 = | h"(ммH2O) | | | | | | |
| lg h' | | | | | | |
Таблица 2
| № | H | h | γ | γср | Δγ | I | (Δγср/γср)·100% |
|---|
| Ед.изм | | | | | | | |
| 1 | | | | | | | |
Контрольные вопросы
- Что называется удельной, молярной теплоемкостями? Каковы единицы их измерений?
- Что понимают под теплоемкостями Ср и Сv? Какая из теплоемкостей Ср и Cv больше и почему?
- Какой процесс называется адиабатическим? Запишите уравнение Пуассона.
- Что происходит с внутренней энергией газа при адиабатическом процессе?
- Как практически может быть реализован адиабатический процесс?
- Какие газовые процессы наблюдаются при проведении опыта?
- Что такое число степеней свободы? Как это число связано с γ? Зная γ (из опыта), рассчитайте число степеней свободы молекул воздуха.
- Объясните определение величины h.
|