Тема №6 Способы преобразования чертежа
1. Классификация способов преобразования
2. Способ вращения вокруг проецирующей оси
3. Способ замены плоскостей проекций
Контрольные вопросы
Контрольные задания по теме: Рабочая тетрадь задача 50
1. Классификация способов преобразования
Трудоемкость и точность графического решения задач часто зависит не только от сложности задач, но и от того, какое положение занимают геометрические фигуры по отношению к плоскостям проекций. Наиболее выгодными являются положения, параллельные плоскостям проекций или перпендикулярные им.
Переход от общего положения геометрической фигуры к частному можно осуществить двумя путями:
а) перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения;
б) выбором новой плоскости проекций, по отношению к которой фигура, не имеющая своего положения в пространстве, окажется в частном положении. Первый путь лежит в основе способа плоскопараллельного перемещения, а второй - в основе способа замены плоскостей проекций.
Существует несколько способов плоскопараллельного перемещения:
1. Способ параллельного перемещения. При этом плоскости, по которым двигаются точки фигуры, параллельны плоскости проекций. Траектория - произвольная плоская линия;
2. Способ вращения вокруг оси, перпендикулярной к плоскости проекций. Траектории перемещаемых точек - дуги окружностей, центры которых находятся на оси вращения;
3. Способ вращения вокруг оси параллельной плоскости проекций (вокруг линии уровня).
2. Способ вращения вокруг проецирующей оси
Это частный случай параллельного перемещения. За траекторию движения точки принимается не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между осью вращения и данной точкой.
При вращении точки вокруг оси перпендикулярной, П2, фронтальная проекция точки перемещается по окружности, а горизонтальная - по прямой, перпендикулярной оси вращения. Если же точка вращается вокруг оси, перпендикулярной П1, то в горизонтальной плоскости траекторией ее движения будет окружность, а во фронтальной – прямая, перпендикулярная оси вращения. На рисунке 32 показано построение новых проекций точек при помощи способа вращения. На рисунке 32 а – вращение вокруг фронтально-проецирующей оси, на рисунке 32 б – вокруг горизонтально-проецирующей оси.

Рисунок 32
Этим способом удобно находить натуральные величины отрезков и фигур, занимающих проецирующее положение.
На рисунке 33 показан пример определения натуральной величины треугольника АВС, плоскость которого перпендикулярна П2. За ось вращения необходимо взять фронтально-проецирующую прямую, проходящую через точку, принадлежащую этой плоскости. В данном случае выбрана точка А - вершина треугольника. Плоскость треугольника вращается во фронтальной плоскости вокруг оси до положения, параллельного горизонтальной плоскости. Во фронтальной плоскости точки С и В перемещаются по окружностям, радиус которых равен расстоянию от оси вращения до фронтальных проекций точек. В горизонтальной плоскости траектории движения точек – прямые, перпендикулярные оси. Полученная проекция треугольника А´В´С´, является его натуральной величиной.

Рисунок 33
Способ вращения наиболее часто применяется при определении натуральных величин сечений поверхностей плоскостями частного положения.
3. Способ замены плоскостей проекций
Сущность этого способа состоит в том, что положение фигуры в пространстве не меняется, а вводится новая система плоскостей проекций. Новая плоскость проекции выбирается перпендикулярно к одной из старых. При этом, проецируемая фигура по отношению к новой плоскости занимает частное положение, обеспечивая наиболее удобное решение задачи. Если замена одной плоскости не обеспечивает требуемый результат, то новую плоскость заменяют еще раз.
На рисунке 34 показано построение проекции точки А в новой системе плоскостей проекций при замене плоскости П1 на П4. Плоскость П4 перпендикулярна П2. Проекция точки А1 заменяется на А4. По линии связи откладывается расстояние от заменяемой проекции точки до новой оси.
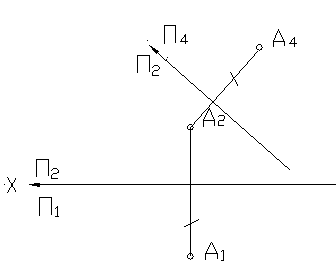
Рисунок 34
На рисунке 35 дан пример определения натуральной величины отрезка общего положения. Новая плоскость П4 выбирается параллельно одной из проекций отрезка. При этом проекция отрезка на эту плоскость будет являться его натуральной величиной.
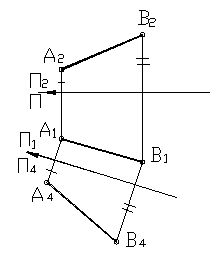
Рисунок 35
В некоторых случаях требуется замена двух плоскостей проекции. Например, при определении расстояния от точки до прямой. При этом прямую необходимо спроецировать в точку. На рисунке 36 отрезок общего положения переведен в проецирующее положение по отношению к плоскости П5.

Рисунок 36
Контрольные вопросы
1. Назовите, какие вы знаете способы преобразования чертежа. Для чего они применяются?
2. Какие задачи можно решать при помощи способа вращения вокруг проецирующей оси?
3. По каким линиям перемещаются проекции точки при вращении вокруг горизонтально проецирующей оси?
4. Можно ли определить натуральную величину фигуры общего положения способом вращения вокруг проецирующей оси?
5. В чем суть способа замены плоскостей проекций?
6. Как построить проекцию точки в новой системе плоскостей проекций? Этапы построения.
7. Сколько замен нужно осуществить, чтобы перевести отрезок общего положения в проецирующее положение?
8. Как нужно выбрать новую плоскость, для того, чтобы сделать плоскость общего положения проецирующей?
|