Тема №7 Поверхности

1. Способы образования поверхностей

2. Классификация поверхностей

3. Гранные поверхности

Контрольные вопросы

Контрольные задания по теме:
Рабочая тетрадь задача 58а, задача 58б

1. Способы образования поверхностей

Мир поверхностей очень разнообразен. Они играют огромную роль в науке, архитектуре и технике. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением типа F(x, y, z)=0, где F(x, y, z) многочлен n-й степени. Степень многочлена определяет порядок поверхности. Например, прямую линию можно назвать поверхностью первого порядка. Поверхности второго порядка – это поверхности, состоящие из плоскостей и также некоторые поверхности вращения.

Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка. Порядок поверхности также может быть определен по числу точек пересечения ее с прямой линией.

В начертательной геометрии фигуры задаются графически, поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Она называется образующей, а линия, вдоль которой она перемещается, – направляющей. Такой способ образования поверхности называется кинематическим.

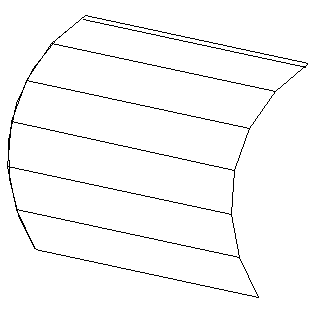
Рисунок 37

На рисунке 37 прямая линия - образующая, а дуга, вдоль которой она перемещается, - направляющая. Другим способом образования поверхности и задания ее на чертеже является задание множества принадлежащих ей точек и линий. Такой способ называется каркасным, а упорядоченное множество точек и линий поверхности называется ее каркасом.

2. Классификация поверхностей

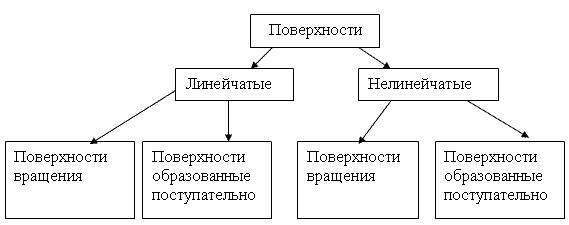
Рисунок 38

Линейчатые поверхности вращения – это конус, цилиндр.

Линейчатые поверхности поступательного движения – все гранные поверхности.

К нелинейчатым поверхностям вращения относятся сфера, шар, эллипсоид. Нелинейчатые поверхности, образованные поступательным движением – это гиперболический параболоид и другие сложные поверхности.

3. Гранные поверхности

Образующей является прямая линия, направляющая – ломаная. Гранная поверхность представляет из себя совокупность пересекающихся плоскостей – граней. Линии пересечения граней – ребра. Точки пересечения ребер – вершины.

Наиболее простой является призматическая поверхность. Она изображена на рисунке 39. Образующая l передвигается вдоль ломаной линии m, которая является направляющей. Все образующие поверхности параллельны.

Рисунок 39

Призмой называется геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которое получается, если призматическую поверхность ограничить двумя основаниями. Основания будут иметь форму многоугольников, боковые грани параллелограммов. Если плоскости основания перпендикулярны боковым граням, то призма называется прямой, если нет то наклонной. Если в основании призмы лежит правильный многоугольник, то призма называется правильной.

Пирамидальная поверхность изображена на рисунке 40. Один конец образующей l неподвижен, а другой передвигается вдоль ломаной линии m.

Рисунок 40

Пирамидой является геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которая будет называться основанием. Точка S-вершина пирамиды. Боковые грани – треугольники. Пирамида будет называться правильной, если в основании лежит правильный многоугольник, а высота опущенная из вершины попадает в центр основания.

Контрольные вопросы

1. Что называется поверхностью? Какие способы образования поверхностей вы знаете?

2. Назовите линейчатые поверхности вращения.

3. Какие нелинейчатые поверхности вы знаете?

4.Какая линия является направляющей у гранных поверхностей, какая является образующей?

5. Как образуется поверхность пирамиды, призмы?

6. Какая призма называется прямой?