Тема №8 Сечение гранных поверхностей плоскостями
1. Построение сечения призмы плоскостью частного положения
2. Построение развертки призмы
3. Построение сечения пирамиды плоскостью частного положения
4. Построение развертки усеченной части пирамиды
Контрольные вопросы
Контрольные задания по теме: эпюр № 2, эпюр № 3 (вариант назначает преподаватель)
1. Построение сечения призмы плоскостью частного положения
Сечением называют плоскую фигуру, которая получается при пересечении поверхности с плоскостью.
Определение проекций сечения следует начинать с построения опорных точек, расположенных на очерковых образующих поверхности, на ребрах, осях симметрии.
На рисунке 41 показано построение сечения прямой треугольной призмы плоскостью S, которая является фронтально – проецирующей. При этом фронтальная проекция сечения уже определена - это линия (1,2,3). Точки 1, 2, 3 - точки пересечения плоскости с ребрами призмы, - называются опорными.

Рисунок 41
Горизонтальная проекция сечения совпадает с проекцией призмы, так как грани призмы являются горизонтально – проецирующими плоскостями. На профильной плоскости проекции точек сечения находим по линиям связи на соответствующих ребрах. Точка 1 принадлежит ребру А, точка 2 – ребру В, и 3 – ребру С. Проекции точек соединяем с учетом видимости. Линия ВС на профильной плоскости невидима, так как она принадлежит грани, которая на профильной плоскости невидима.
Натуральную величину сечения находим способом вращения. Ось вращения удобно выбрать в точке 1. Секущая плоскость поворачивается до положения, параллельного горизонтальной плоскости проекций. Из горизонтальных проекций точек сечения проводим линии перпендикулярно оси вращения или параллельно оси Х. И, таким образом, на горизонтальной плоскости получим натуральную величину сечения.
2. Построение развертки призмы
Построим полную развертку призмы. Она будет состоять из прямоугольников, которыми являются боковые грани, и двух треугольников – верхнего и нижнего оснований. На развертке откладываются только натуральные величины сторон и углов. Натуральную величину боковых ребер – высоту призмы, возьмем на фронтальной проекции, а натуральные величины сторон основания – с горизонтальной проекции, так как основания параллельны горизонтальной плоскости.
Для того чтобы построить развертку усеченной части призмы, необходимо отметить на ней точки 1, 2, 3 и убрать часть, отсеченную плоскостью S. Затем пристроить к развертке натуральную величину сечения. Развертка усеченной части призмы изображена на рисунке 42.

Рисунок 42
3. Построение сечения пирамиды плоскостью частного положения
Возьмем правильную четырехгранную пирамиду и построим ее сечение фронтально – проецирующей плоскостью S. Находим проекции опорных точек – точек пересечения ребер с секущей плоскостью. На рисунке 43 изображены три проекции сечения пирамиды и требуемые построения.

Рисунок 43
Натуральную величину сечения пирамиды строим методом вращения вокруг проецирующей оси. Ось вращения выбираем проходящей через точки 1 и 2 секущей плоскости. Построения проводим аналогично примеру с призмой.
4. Построение развертки усеченной части пирамиды
Отметим точку S0 – вершину пирамиды и проведем из нее луч в произвольном направлении. На этом луче отложим натуральную величину любого бокового ребра, например АS. Оно параллельно фронтальной плоскости проекций, поэтому величина А2S2 будет являться натуральной величиной ребра SА, а так как пирамида правильная, то все ее боковые ребра равны. Затем строим треугольник, соответствующий боковой грани АSВ. Натуральную величину стороны SВ возьмем с горизонтальной проекции пирамиды, так как ее основание параллельно горизонтальной плоскости. Затем строим развертки остальных граней.
На боковых ребрах и сторонах основания откладываем высоты точек сечения и пристраиваем натуральную величину сечения. На рисунке 44 построена полная развертка усеченной части пирамиды.
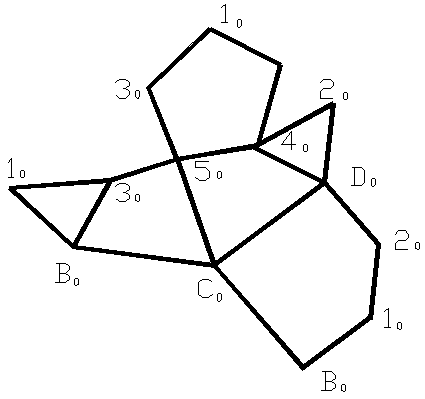
Рисунок 44
Контрольные вопросы
1. Какие точки нужно выбрать для построения проекций сечения призмы плоскостью частного положения?
2. С чем совпадает горизонтальная проекция сечения прямой призмы фронтально проецирующей плоскостью?
3. Для чего нужна базовая плоскость?
4. Какую фигуру представляет развертка боковой поверхности призмы?
5. Как построить проекции точки, принадлежащей боковой грани пирамиды?
6. Каким образом строится развертка пирамиды?
|