Тема №10 Сечение поверхностей вращения плоскостями частного положения
1. Построение сечения цилиндра
2. Построение развертки цилиндра
3. Построение сечения конуса. Определение натуральной величины сечения
4. Построение развертки усеченной части конуса
Контрольные вопросы
Контрольные задания по теме:
Рабочая тетрадь задача 68, задача 69
1. Построение сечения цилиндра
Цилиндром будет называться геометрическое тело, полученное при ограничении цилиндрической поверхности двумя параллельными плоскостями - основаниями цилиндра. Если в основании цилиндра лежит окружность, а образующая перпендикулярна основанию, то цилиндр называется прямым круговым.
Линия сечения строится также при помощи опорных точек - точек пересечения секущей плоскости с очерковыми образующими и осью цилиндра. Но необходимо взять также промежуточные точки для более точного построения линии сечения. На рисунке 49 показано построение проекций сечения цилиндра фронтально - проецирующей плоскостью S. Так как цилиндр является проецирующей поверхностью, то горизонтальная проекция сечения совпадает с секущей плоскостью и на профильной проекции получим эллипс. Точки 2 и 3 будут являться границей видимости линии сечения для профильной плоскости.
Натуральную величину сечения можно определить способом вращения. Ось вращения выбираем в точке 1 и вращаем секущую плоскость до положения, параллельного горизонтальной плоскости. На горизонтальной плоскости получим эллипс, который будет являться натуральной величиной сечения цилиндра.

Рисунок 49
2. Построение развертки цилиндра
Разверткой цилиндра является прямоугольник с высотой, равной высоте цилиндра, и длиной, равной длине окружности основания 2πR. Для того, чтобы построить развертку усеченной части, основание цилиндра делят на равные части, тем самым аппроксимируя цилиндрическую поверхность призматической. Разделим окружность основания на 12 равных частей и отложим их вдоль горизонтальной линии развертки, по вертикали отложим высоту цилиндра (рис. 50).
Затем на полученных образующих отметим высоты точек сечения. Пристроим окружность основания и натуральную величину сечения.
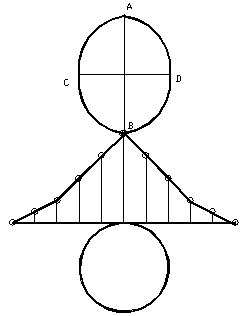
Рисунок 50
3. Построение сечения конуса. Определение натуральной величины сечения
Конус - это геометрическое тело, полученное путем ограничения конической поверхности плоскостью. Если в основании конуса лежит окружность, а высота попадает в центр основания, то конус называется прямым круговым.
На рисунке 51 построено сечение конуса фронтально - проецирующей плоскостью. Точки сечения находим при помощи вспомогательных секущих плоскостей. Точки С и D являются границей видимости для профильной проекции сечения.
Натуральную величину сечения находим способом вращения. Ось вращения выбираем в точке D и поворачиваем секущую плоскость до положения, параллельного горизонтальной плоскости проекций. Из горизонтальных проекций точек проводим линии, перпендикулярные оси вращения. Натуральной величиной сечения будет являться эллипс.

Рисунок 51
4. Построение развертки усеченной части конуса
Развертка конуса является круговым сектором с радиусом, равным длине образующей конуса и длиной дуги, равной длине окружности основания конуса. Делим основание конуса на 12 равных частей и откладываем их по дуге на развертке. Затем на соответствующих образующих нужно отложить натуральные величины высот точек сечения. Чтобы получить полную развертку усеченной части, пристраиваем основание и натуральную величину сечения. На рисунке 52 показано построение развертки конуса.
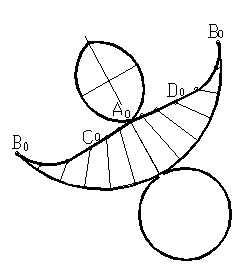
Рисунок 52
Контрольные вопросы
1. Как образуется цилиндрическая поверхность?
2. Если секущая цилиндр плоскость фронтально проецирующая, то где будут лежать горизонтальные проекции точек сечения?
3. Какими способами можно определять натуральную величину фигуры сечения?
4. Какой геометрической фигурой является развертка боковой поверхности цилиндра? Конуса?
5. Для чего нужно разбивать окружность основания на некоторое количество равных частей?
6. Как построить развертку конической поверхности?
7. Как получить из полной развертки поверхности развертку ее усеченной части?
|