МОДУЛЬ 3. Управление в логистике

ТЕМА 3.4. Применение методов
прогнозирования в логистике

3.4.1. Основные положения теории прогнозирования

3.4.2. Примеры прогноза текущего запаса на складе

3.4.3. Комбинированный прогноз

Вопросы для повторения

3.4.1. Основные положения
теории прогнозирования

В снабженческой, производственной и распределительной логистиках широко используются методы прогнозирования, поскольку значения прогнозных оценок развития анализируемых процессов или явлений являются основой принятия управленческих решений при оперативном, тактическом и стратегическом планировании. Очевидно также, что точность и надежность прогноза определяет эффективность реализации различных логистических операций и функций – от оценки вероятности дефицита продукции на складе до выбора стратегии развития фирмы.

Известно, что теория прогнозирования включает анализ объекта прогнозирования; методы прогнозирования, подразделяющиеся на математические (формализованные) и экспертные (интуитивные); системы прогнозирования, в частности непрерывного, при котором за счет мониторинга осуществляется корректировка прогнозов в процессе функционирования объекта.

Одним из основных классификационных признаков является также период прогноза, при этом большинство авторов выделяют три вида прогнозов: краткосрочный, среднесрочный и долгосрочный. Естественно, что временные интервалы прогнозов зависят от природы объекта, т. е. изучаемой области деятельности. Так, при рассмотрении технико-экономических показателей деятельности фирм период краткосрочного прогноза не превышает 1 года, среднесрочного прогноза – от 1 до 5 лет, долгосрочного – свыше 5 лет.

Математические методы прогнозирования подразделяются на три группы:

1. симплексные (простые) методы экстраполяции по временным рядам;
2. статистические методы, включающие корреляционный и регрессионный анализ и др.;
3. комбинированные методы, представляющие собой синтез различных вариантов прогнозов.

Прогнозы I типа (в «узком» смысле):

• осуществляются с применением симплексных или статистических методов на основе временных рядов;
• число значимых переменных включают от 1 до 3 параметров, т. е, по масштабности они относятся к сублокальным прогнозам;
• при использовании одного параметра, например, времени, такие прогнозы считаются сверхпростыми, при двух-трех взаимосвязанных параметрах – сложными;
• по степени информационной обеспеченности периода ретроспекции прогнозы I типа могут быть отнесены к объектам с полным информационным обеспечением.

Для повышения точности и достоверности прогнозных оценок I типа целесообразно использование комбинированных методов, при этом желательно использование большого количества вариантов прогноза, рассчитанных на основе различных подходов или альтернативных источников информации.

Прогноз II типа (в «широком» смысле) подразумевает, что исходные данные для получения оценок определяются с использованием опережающих методов прогнозирования: «патентного», публикационного и др. Как правило, прогнозы II типа используются для долгосрочного прогнозирования и разбиваются на два этапа: первый – получение прогнозных оценок основных факторов; второй – собственно прогноз развития процесса или явления. Учитывая объективную сложность и трудоемкость выполнения прогнозов II типа, можно констатировать, что наибольшее распространение получили методы прогнозирования I типа.

Наиболее часто для прогнозирования I типа используется метод экстраполяции. В общем случае модель прогноза включает три составляющие (рис. 3.4.1) и записывается в виде:

(3.4.1)

где y_t – прогнозные значения временного ряда;

– среднее значение прогноза (тренд);

v_t – составляющая прогноза, отражающая сезонные колебания (сезонная волна);

ε_t – случайная величина отклонения прогноза.

Рис. 3.4.1. Прогнозирование на основе временных рядов:
1 – экспериментальные данные на интервале наблюдения (A);
2 – тренд; 3 – тренд и сезонная волна;
4 – значение точечного прогноза на интервале упреждения (B);
5 – интервальный прогноз

В частных случаях количество составляющих модели меньше, например, только и v_t.

Подробно вопросы прогнозирования с использованием методов экстраполяции изложены в ряде работ, но ввиду отсутствия общепринятого алгоритма обработки временных рядов может быть предложена следующая последовательность расчета:

1. На основе значений временного ряда на предпрогнозном периоде (интервале наблюдения) с использованием метода наименьших квадратов определяются коэффициенты уравнения тренда y_t, видом которого задаются. Обычно для описания тренда используются полиномы различных порядков, экспоненциальные, степенные функции и т. п.
2. Для исследования сезонной волны значения тренда исключаются из исходного временного ряда. При наличии сезонной волны определяют коэффициенты уравнения, выбранного для аппроксимации v_t.
3. Случайные величины отклонения ε_t определяются после исключения из временного ряда значений тренда и сезонной волны на предпрогнозном периоде. Как правило, для описания случайной величины ε_t используется нормальный закон распределения.
4. Для повышения точности прогноза применяются различные методы (дисконтирование, адаптация и др.). Наибольшее распространение в практике расчетов получил метод экспоненциального сглаживания, позволяющий повысить значимость последних уровней временного ряда по сравнению с начальными.

3.4.2. Примеры прогноза
текущего запаса на складе

Рассмотрим применение методов прогнозирования на основе данных расхода деталей на складе. В табл. 3.4.1 приведены три реализации текущего расхода; для каждой реализации даны величины расхода за день характеристики, представляющие собой расход деталей со склада за соответствующий цикл.

Таблица 3.4.1

Проиллюстрируем возможные варианты прогнозов для одной реализации.

Пример 3.4.1. Воспользуемся первой реализацией. Допустим, что нам известны значения расхода деталей со склада за пять дней работы (табл. 3.4.2).

Таблица 3.4.2

Исходные данные и результаты расчета
коэффициентов уравнения (3.4.2) при N=5

ti, дн.	yi, ед.		yiti	Прогноз yi*	(yt–yi)2
1	41	1	41	42	1
2	39	4	78	39	0
3	38	9	114	36	4
4	35	16	140	33	4
5	28	25	140	30	4
Суммы

* Значения округлены

Выберем уравнение тренда y_t в виде линейной зависимости:

(3.4.2)

Расчет коэффициентов уравнения и производится по формулам, полученных на основе метода наименьших квадратов:

(3.4.3)

(3.4.4)

Находим: a₀ = 45,2, a₁ = –3,0. Таким образом, уравнение прогноза пишется в виде:

(3.4.5)

Для оценки границ интервального прогноза необходимо рассчитать среднее квадратичное отклонение σ_t:

(3.4.6)

Подставляя значения в формулу, находим σ_t:

(3.4.7)

На основании полученных зависимостей y_t и σ_t рассчитываются прогнозные оценки:

1. среднего времени расхода текущего запаса ;
2. страхового запаса y_c с заданной доверительной вероятностью Р.

Расчет прогнозной величины среднего времени расхода производится по формуле

(3.4.8)

Приняв y_t = 0, находим :

Для расчета страхового запаса воспользуемся формулой:

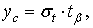(3.4.9)

где σ_t – среднее квадратичное отклонение,

t_β – параметр нормального закона распределения, соответствующий доверительной вероятности β.

Параметр t_β определяет для нормального закона число средних квадратических отклонений, которые нужно отложить от центра рассеивания (влево и вправо) для того, чтобы вероятность попадания в полученный участок была равна β.

В нашем случае доверительные интервалы откладывают вверх и вниз от среднего значения уt. .

В табл. 3.4.3 приведены наиболее часто встречающиеся в практических расчетах значения вероятности β и параметра t_β для нормального закона распределения.

Таблица 3.4.3

Страховой запас рассчитывается так же, как и границы интервального прогноза. Для рассматриваемого примера при доверительной вероятности β=0,9 находим по табл. 3.4.3 t_β = 1,643. Тогда величина страхового запаса составит:

Примем y_c=3,0.

На рис. 3.4.2 приведены границы интервального прогноза при β = 0,9.

Рис. 3.4.2. Прогноз текущего расхода деталей на складе (N = 5):
1 – исходные данные; 2 – уравнение тренда;
3, 3' – границы интервального прогноза; 4 – время расхода запаса

Рассчитанное значение страхового запаса соответствует только одному дню наступления дефицита, а именно согласно прогнозу T = 15. Для учета возможных нарушений срока поставки необходимо также при расчете страхового запаса оценить влияние задержки, связанной с выполнением заказа, в частности с транспортировкой.

К сожалению, по одной реализации невозможно оценить вероятностный характер длительности функциональных циклов поставки. Однако можно предположить, что выявленная тенденция расхода запаса сохранится. В этом случае для оценки прогнозной величины страхового запаса можно воспользоваться формулой

(3.4.10)

где τ – параметр, характеризующий количество дней задержки поставки заказа.

Рассчитаем величину страхового запаса при условии задержки на один день по сравнению с прогнозной оценкой T = 15 дней, т. е. на 16-й день:

Аналогично, при τ = 2 (17 день)

Для оценки вероятности отсутствия дефицита допускается, что отклонения ежедневного расхода деталей от среднего значения (тренда) подчиняются нормальному закону распределения. Тогда, пользуясь уравнением функции нормального закона, определяют вероятность отсутствия дефицита:

(3.4.11)

где y_t – уравнение тренда;

σ – среднее квадратическое отклонение.

В табл. 3.4.4 приведен ряд значений функции Ф(х) и Р(х).

Таблица 3.4.4

Появление дефицита означает, что текущая величина запаса на складе равна нулю, т. е. у = 0.

Для определения вероятности отсутствия дефицита необходимо:

1. рассчитать ,
2. по табл. 3.4.4 с помощью х найти Р(х).

Для рассматриваемого примера рассчитаем вероятности отсутствия дефицита деталей на складе на 13-й, 14-й и 15-й дни. Так, для T = 13 получаем:

По табл. 3.4.4 находим Р_Т=13 > 0,999, т. е, вероятность отсутствия дефицита ничтожно мала.

Аналогично, для T = 14 получим y_Т=14 = 3,2, x = –1,78, и вероятность отсутствия дефицита Р_Т=14 = 0,95.

Наконец, для T = 15 вероятность отсутствия дефицита Р = 0,5.

Следует подчеркнуть, что так же, как при оценке прогнозной величины страхового запаса, определение вероятности отсутствия дефицита по одной реализации справедливо только при строгом соблюдении сроков поставки. Если они не соблюдаются, то расчет должен проводиться с учетом рассеивания длительности функциональных циклов поставки.

В заключение определим ошибку прогноза среднего времени Т:

(3.4.12)

где T_ф, T_п – соответственно фактическая и прогнозная продолжительность цикла, дн.

Получим:

Ошибка прогноза велика, но это закономерно, так как нарушено одно из эмпирических правил экстраполяционного прогнозирования: между предпрогнозным периодом t и периодом упреждения (прогноза) τ = T – t должно соблюдаться соотношение:

(3.4.13)

При T = 5 допустимая величина времени прогноза:

Следовательно, величина надежного прогноза соответствует T ≈ 7 дн. и период упреждения составляет τ = 2 дн.

Пример 3.4.2. Считается, что средняя длина функционального цикла расхода запасов составляет T = 10 дн. Тогда t = 7,5 дн.

Увеличим длину динамического ряда до N = 7 (рис. 3.4.3).

Рис. 3.4.3. Прогноз текущего расхода деталей на складе (N = 7):
1 – исходные данные; 2 – уравнение тренда;
3, 3' – границы интервального прогноза; 4 – время расхода запаса

Выполним расчеты аналогично примеру 3.4.1, полученные данные занесем в табл. 3.4.5.

Таблица 3.4.5

Исходные данные и результаты расчета
коэффициентов уравнения тренда при N=7

ti	yi		yiti	yi	(yt–yi)2
1	41	1	41	43,1	4,41
2	39	4	78	39,2	0,04
3	38	9	114	35,3	7,29
4	35	16	140	31,4	12,96
5	28	25	140	27,6	0,25
6	23	36	138	23,6	0,36
7	19	49	133	19,7	0,49
Суммы

,

Получим уравнение тренда:

Соответственно,

Рассчитаем среднее прогнозное время расхода запаса со склада

Рассчитаем величину страхового запаса y_c для 12-го, 13-го и 14-го дней. Примем β = 0,95, т. е, t_β = 1,96. Тогда:

Определим вероятность дефицита на складе на 10-й день. Находим ; по табл. 3.4.4 , т.е. наличие дефицита маловероятно. Аналогично, для для .

В заключение можно сделать следующее замечание: рассчитанные величины среднего запаса получены при условии, что наблюдающая величина дефицита и вариация ежедневного расхода – независимые величины. Несомненно, это допущение требует проверки.

3.4.3. Комбинированный прогноз

На формирование стратегии автотранспортного предприятия (АТП) на рынке влияют факторы как внешней, так и внутренней среды, в том числе определяющие состояние спроса на услуги. Основным является вопрос о потенциальных возможностях предприятия, определяемых технико-технологическими и организационно-финансовыми факторами среды. Принципиальное различие между предъявляемыми к перевозке грузами (или спросом) и провозными возможностями АТП состоит в том, что первое следует отнести к условиям внешней среды, т. е. «природе», состояние которой формируется под действием большого количества факторов и в подавляющем большинстве случаев не зависит от транспортной политики конкретного АТП (если рассматриваемое предприятие не является монополистом в данном сегменте рынка транспортных услуг), а второе определяется политикой и тактикой действий предприятия, не имея случайного характера, а, скорее, подчиняясь неким внутренним закономерностям. Таким образом, под влиянием случайных факторов объем перевозок представляет собой случайную величину, подчиняющуюся определенному закону или функции распределения F(Q). Введение функции распределения для описания состояния «природы» позволяет, согласно теории статистических решений, использовать вероятностные критерии принятия решений в условиях риска.

Что касается состояния АТП, то оно может быть представлено в виде различных стратегий A_i, каждая из которых количественно характеризуется числом автомобилей N_i и их провозными возможностями W_i.

Указанные стратегии A_i, являются дискретными величинами, если используется число автомобилей N, или непрерывными за счет варьирования показателей, входящих в расчет производительности автомобиля W_i.

Связь между A_i стратегией и объемом перевозок Q_i определяется в виде матрицы (табл. 3.4.6), элементы которой (a_ij) отражают «выигрыш», получаемый АТП при выборе i-й стратегии.

Таблица 3.4.6

В ряде работ, где предпринимались попытки использования теории статистических решений для конкретных хозяйственных объектов, в качестве элемента матрицы a_ij – «выигрыша» – использовались условные величины. В качестве «выигрыша» могут быть использованы различные экономические показатели: доход, прибыль и другие, а также показатели, способствующие усилению конкурентных или рыночных позиций, усилению влияния на клиентуру и укреплению имиджа предприятия, улучшению качества производимых услуг.

Возможны три соотношения между объемом перевозок Q_i и стратегией предприятия А. Первое – – состояние «выигрыша»; второе – – нейтральное состояние; третье – – состояние «проигрыша». Величина – вероятностное отклонение за счет случайного характера величин, определяющих значение элементов матрицы. Теоретически возможен вариант, когда области значений a_ij будут расположены иным образом, чем это показано на рис. 3.4.4.

Рис. 3.4.4. Распределение на различные области матрицы стратегий АТП:
1 – «выигрыш», 2 – нейтральное состояние, 3 – «проигрыш»

В частности, введение оценки «упущенной выгоды» может изменить границы областей 1-3. Считается, что наилучшей стратегией A = A_i является та, при которой показатель A_i обращается в максимум:

(3.4.14)

где Q_j = F(Q_j) – вероятность j-го состояния «природы».

Таким образом, оптимальная стратегия АТП может быть определена при наличии F(Q_j) и матрицы стратегий a_ij.

Рассмотрим возможные варианты расчета F(Q_j). Традиционно для количественной оценки прогноза Q_j, используется метод экстраполяции по динамическим рядам с использованием полиномов различной степени.

Результаты прогноза представляются в виде среднего значения Q и дисперсии D_Q, по которым определяется вид функции распределения F(Q_j). Далее c использованием условия максимизации A_i выбираем стратегию АТП.

Основная трудность использования вышеописанной методики – это невысокая точность прогноза, Повышение точности может быть достигнуто за счет комбинированных методов прогноза, предусматривающих синтез двух и более прогнозных вариантов.

Каждый метод прогнозирования обладает определенной достоверностью, имеет свои преимущества и недостатки, Считается, что комбинированные методы прогнозирования (синтез прогнозов) позволяют компенсировать недостатки одних способов достоинствами других. На рис. 3.4.5 представлена блок-схема комбинированного прогноза для двух вариантов прогноза, один из которых – прогноз, выполненный эвристическим методом, основанным на статистической обработке мнений экспертов.

Рис. 3.4.5. Блок-схема выбора стратегии АТП
в целевом сегменте рынка транспортных услуг

Процедура получения экспертных оценок может быть формализована и представлена в виде блок-схемы (рис. 3.4.6).

Рис. 3.4.6. Блок-схема прогноза на основе экспертных опросов

Рассмотрим некоторые блоки подробнее.

Формирование группы экспертов – важнейшая составляющая экспертного метода. Не останавливаясь подробно на вопросах персонального подбора, затронем только количественную сторону, а именно число экспертов. Известно, что при прогнозировании в целях минимизации расходов на прогноз стремятся привлекать минимальное число экспертов при условии обеспечения ошибки результата прогнозирования не более Е, где 0 < Е < 1. Поэтому рекомендуемое число экспертов может быть определено по формуле:

(3.4.15)

При подстановке предельных значений Е находим:

Таким образом, минимальное количество экспертов равно 4. Для определения максимальной численности экспертной группы используется неравенство:

(3.4.16)

где K_i – компетентность i-го эксперта, рассчитываемая на основе анкеты самооценки;

K_max – максимально возможная компетентность по используемой шкале компетентности экспертов.

Статистический анализ результатов опроса предусматривает проведение двух взаимосвязанных процедур: традиционной статистической обработки в виде средних значений, дисперсий и т. п., а также оценки всей экспертной группы – степени согласованности, взаимосвязи и других показателей мнений экспертов. Оценка группы экспертов проводится с использованием части полученных статистических оценок. Если последние не удовлетворяют соответствующим критериям, то в блок-схеме предусмотрена корректировка, которая приводит, в частности, к изменению состава экспертов и повторной процедуре опроса.

Методика статистической обработки данных включает следующие этапы:

1. Определение для каждого фактора суммы рангов:

(3.4.17)

где a_ij – ранг, присвоенный j-м экспертом i -му фактору;

m – число экспертов.

2. Определение средней величины суммы рангов:

(3.4.18)

где k – число факторов.

3. Определение суммы квадратов отклонений:

(3.4.19)

4. Определение коэффициента конкордации W, позволяющего оценить степень согласованности мнений экспертов (при отсутствии равных рангов):

(3.4.20)

Если W существенно отличается от нуля, то можно полагать, что между оценками экспертов существует определенное согласие.

5. Оценка неслучайности согласия мнений экспертов производится с помощью критерия Пирсена по величине при числе степени свободы n = k – 1 и заданном уровне значимости α:

(3.4.21)

где – табличное значение.

В случае соблюдения неравенства с доверительной вероятностью можно утверждать, что мнения экспертов относительно вероятности факторов согласуются неслучайно.

Представленный вариант получения прогноза на основе экспертных оценок является универсальным и в случае использования баллов заканчивается построением ранжированной диаграммы рангов.

Для перехода к конкретному прогнозу, в частности объема перевозок, последовательности расчета сводятся к следующему:

1. Составляется ряд интервальных значений Q_j возможных объемов перевозок для рассматриваемого клиента; разбивка на n интервалов осуществляется на основе F(Q_j).
2. Эксперты оценивают значимость каждого Q_j с использованием баллов, шкала которых охватывает n интервалов, т.е. j = 1, 2, …, n.
3. Проводится статистическая обработка оценок экспертов, и после ранжирования каждому Q_j присваивается новый номер в порядке убывания, т.е. интервалу Q_j с наименьшей суммой баллов присваивается номер 1 и т.д.

   Полагаем, что интервалу Q_j соответствует наиболее правдоподобная гипотеза (П₁), затем вторая ( (П₂) и т.д.

4. Вероятности гипотез (П₁), (П₂ ), …., (П_n) определяются по формуле:

(3.4.22)

5. Восстанавливается функция распределения экспертного прогноза объема перевозок F(Q_эj).
6. Для восстановленной «экспертной» функции находятся среднее значение и дисперсия D_эq.

   Значения весовых коэффициентов для определения комбинированных оценок вероятностей каждого интервала находим по формулам:

(3.4.23)

где μ₁ и D_q – весовой коэффициент и дисперсия экстраполяционного прогноза;

μ₂ и D_эq – весовой коэффициент и дисперсия экспертного прогноза.

7. Вероятности F(Q_j) для комбинированного прогноза рассчитываются следующим образом:

(3.4.24)

Вопросы для повторения

1. Классификация методов прогнозирования.
2. Суть прогноза текущего расхода деталей на складе.
3. Расчет страхового запаса.
4. Метод комбинированного прогноза.