Вычисление предела дробно-рациональной функции
Чтобы найти предел дробной рациональной функции
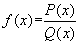 при
при 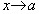 , необходимо подставить предельное значение аргумента
, необходимо подставить предельное значение аргумента 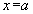 в данную функцию.
в данную функцию.
Если при этом знаменатель отличен от нуля, то пределом будет частное:
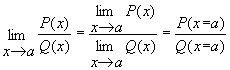 .
.
Если числитель имеет предел А, отличный от нуля, а знаменатель стремится
к нулю, то пределом функции будет бесконечность: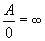 .
.
Если числитель и знаменатель данной функции при 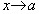 есть величины бесконечно малые
есть величины бесконечно малые 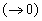 , то для того, чтобы найти предел, необходимо предварительно преобразовать данное выражение: многочлены:
, то для того, чтобы найти предел, необходимо предварительно преобразовать данное выражение: многочлены:
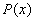 и
и 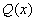 надо разложить на множители и затем сократить на множитель
надо разложить на множители и затем сократить на множитель
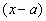 .
.
Пример 1. Найти предел функции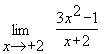 .
.
Здесь знаменатель дробной рациональной функции при 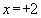 отличен от нуля. Поэтому, заменив аргумент
отличен от нуля. Поэтому, заменив аргумент 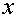 его предельным значением, получим
его предельным значением, получим
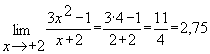 .
.
Пример 2. Найти предел функции 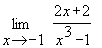 .
.
При 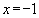 знаменатель отличен от нуля, а числитель есть величина бесконечно малая. Поэтому частное от деления бесконечно малой величины на переменную, имеющую конечный предел, тоже величина бесконечно малая, т.е. предел дроби равен нулю:
знаменатель отличен от нуля, а числитель есть величина бесконечно малая. Поэтому частное от деления бесконечно малой величины на переменную, имеющую конечный предел, тоже величина бесконечно малая, т.е. предел дроби равен нулю:
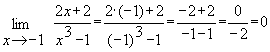 .
.
Пример 3. Найти предел функции 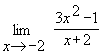 .
.
Здесь знаменатель дроби при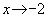 равен нулю, а числитель отличен от нуля, поэтому дробь является бесконечно большой:
равен нулю, а числитель отличен от нуля, поэтому дробь является бесконечно большой:
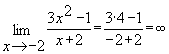 .
.
Пример 4. Найти предел функции 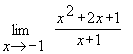 .
При
.
При 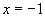 и числитель и знаменатель дроби обращаются в нуль и получается неопределенное выражение вида
и числитель и знаменатель дроби обращаются в нуль и получается неопределенное выражение вида 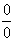 .
.
Чтобы раскрыть эту неопределенность, необходимо предварительно преобразовать данное выражение следующим образом:
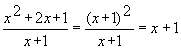 ,
,
т.е. разложить на множители числитель и сократить на общий множитель
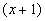 :
:
т.о. 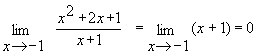 .
.
Чтобы найти предел дробной рациональной функции 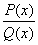 при
при 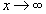 , необходимо подставить
, необходимо подставить 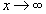 в числитель и знаменатель дроби.
Если при этом получится неопределенное выражение вида
в числитель и знаменатель дроби.
Если при этом получится неопределенное выражение вида 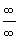 , то необходимо числитель и знаменатель дроби разделить на
, то необходимо числитель и знаменатель дроби разделить на 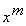 , где
, где 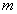 -
наивысшая степень многочленов
-
наивысшая степень многочленов 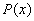 и
и 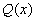 .
.
Пример 5. Найти предел 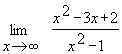 .
.
Разделив числитель и знаменатель на 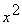 , получим:
, получим:
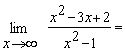
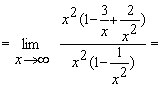
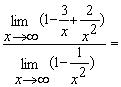
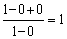 .
.
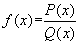 при
при 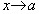 , необходимо подставить предельное значение аргумента
, необходимо подставить предельное значение аргумента 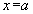 в данную функцию.
в данную функцию.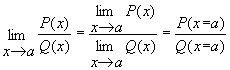 .
.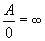 .
.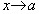 есть величины бесконечно малые
есть величины бесконечно малые 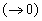 , то для того, чтобы найти предел, необходимо предварительно преобразовать данное выражение: многочлены:
, то для того, чтобы найти предел, необходимо предварительно преобразовать данное выражение: многочлены:
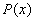 и
и 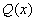 надо разложить на множители и затем сократить на множитель
надо разложить на множители и затем сократить на множитель
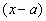 .
.
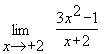 .
.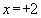 отличен от нуля. Поэтому, заменив аргумент
отличен от нуля. Поэтому, заменив аргумент 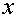 его предельным значением, получим
его предельным значением, получим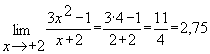 .
.  .
. знаменатель отличен от нуля, а числитель есть величина бесконечно малая. Поэтому частное от деления бесконечно малой величины на переменную, имеющую конечный предел, тоже величина бесконечно малая, т.е. предел дроби равен нулю:
знаменатель отличен от нуля, а числитель есть величина бесконечно малая. Поэтому частное от деления бесконечно малой величины на переменную, имеющую конечный предел, тоже величина бесконечно малая, т.е. предел дроби равен нулю: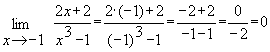 .
.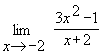 .
.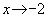 равен нулю, а числитель отличен от нуля, поэтому дробь является бесконечно большой:
равен нулю, а числитель отличен от нуля, поэтому дробь является бесконечно большой:
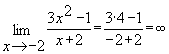 .
.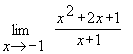 .
При
.
При 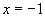 и числитель и знаменатель дроби обращаются в нуль и получается неопределенное выражение вида
и числитель и знаменатель дроби обращаются в нуль и получается неопределенное выражение вида 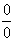 .
. 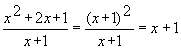 ,
, 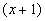 :
: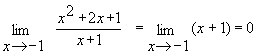 .
.
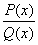 при
при 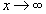 , необходимо подставить
, необходимо подставить 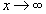 в числитель и знаменатель дроби.
Если при этом получится неопределенное выражение вида
в числитель и знаменатель дроби.
Если при этом получится неопределенное выражение вида 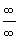 , то необходимо числитель и знаменатель дроби разделить на
, то необходимо числитель и знаменатель дроби разделить на 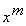 , где
, где 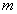 -
наивысшая степень многочленов
-
наивысшая степень многочленов 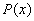 и
и 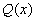 .
. 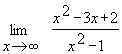 .
.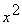 , получим:
, получим:
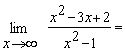
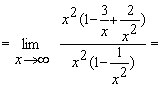
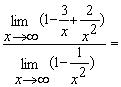
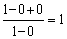 .
.