



ПЛАН:
Умозаключение - форма мышления, посредством которой из одного и более суждений выводится новое суждение.
Истинность заключения обусловлена двумя факторами: во-первых, истинностью посылок, во-вторых, формальной правильностью связи между посылками - правильной формой соответствующего умозаключения.
Истинным является мышление, адекватно отражающее фрагмент действительности, а "правильным" называется мышление, не нарушающее правил и законов формальной логики.
Любое умозаключение состоит из посылок и заключения или вывода из посылок.
Посылки - это исходные суждения, а заключение - новое суждение.
При выявлении логической формы умозаключения посылки и заключение принято записывать столбиком. Посылки отделяются от заключения горизонтальной чертой. Над ней записываются посылки, а под ней - заключение.
Логическим основанием выведения нового суждения является смысловая связь посылок. Они состоят из суждений, состоящих из одинаковых терминов, т. е. связанных по содержанию. Если взять разные по содержанию суждения, то вывод из них невозможен. Например, из суждений "Все планеты - небесные тела" и "Ручка - канцелярский прибор" нельзя сделать заключение. Ни в действительности, ни логически они не связаны.
В зависимости от последовательности движения мысли и логической обоснованности выводного суждения умозаключения делятся на виды:
1) дедуктивные: от более общего знания к менее общему; заключение с логической необходимостью вытекает из посылок, оно ими обосновано полностью и однозначно;
2) индуктивные: от менее общего знания к более общему; заключение имеет чаще всего вероятностный характер;
3) умозаключения по аналогии: от частного знания к частному; заключение носит вероятностный характер.
Дедуктивные умозаключения дают чисто формальные выводы, т.е. по существу лишь раскрывают в новой форме информацию, изначально заложенную в посылках.
Индуктивные выводы и аналогии уступают дедукции в точности, но имеют преимущество в том, что только в них появляется принципиально новое знание.
Простой категорический силлогизм (ПКС) - это дедуктивное умозаключение, в котором из двух категорических суждений выводится новое категорическое суждение.
В силлогизме различают три термина:
Субъект заключения называется меньшим термином (S)
Предикат заключения называется бoльшим термином (Р)
Понятие, которое присутствует в обеих посылках, но отсутствует в заключении называется средним термином (М). Его функция - связать посылки.
Суждение, в которое входит бoльший термин, называется бoльшей посылкой.
Суждение, в которое входит меньший термин, называется мeньшей посылкой.
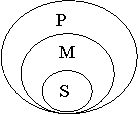
Почему эти термины получили такое название легко увидеть, если изобразить отношение терминов приведенного выше силлогизма при помощи кругов Эйлера. "греки" - S, "люди" - М, "смертны" - Р.
Из диаграммы видно, что названия терминов соответствуют их объемам
Традиционно в силлогизмах сначала указывается бoльшая, а затем мeньшая посылка
Ее суть: Признак признака есть признак самой вещи ( принцип nota notae - признак признака), а то что противоречит признаку вещи, противоречит и самой вещи.
Этой аксиоме предшествует другая аксиома: все что утверждается относительно всего множества, утверждается и относительно каждого его подмножества, и все, что отрицается относительно всего множества, отрицается и относительно каждого его подмножества (в трад. логике этот принцип получил название dictum de omni et nullo - речь обо всем и ни о чем).
I. Правила терминов:
1) в силлогизме должно быть только 3 термина
Термин М должен быть одним и тем же понятием
в обеих посылках, иначе получим ошибку, называемую "учетверением терминов".
Например:
Жизнь - это борьба
Дзюдо - борьба
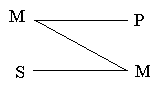
Фигуры силлогизма - это его разновидности, различающиеся положением среднего термина (М) в посылках.
Посылки изображаются горизонтальными отрезками, крайние точки отрезков обозначают термины, а наклонные или вертикальные линии соединяют средний термин в разных посылках)
Возможны 4 варианта таких структур:
Все студенты - люди
Ни один профессор не является студентом

Во 2-й фигуре средний термин занимает место предиката в обеих посылках
Пример:
Этот смертельный удар (Р) нанесен человеком огромной силы (M)
Обвиняемый (S) не является человеком огромной силы (М)
Все физики стремятся к истине
Некоторые историки стремятся к истине

В 3-ей фигуре средний термин занимает место субъекта в обеих посылках.
Пример:
Ни один страус (М) не летает (Р)
Все страусы (М) птицы (S)
Пример:
Все студенты являются людьми
Некоторые студенты не являются мужчинами
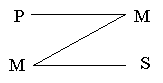
В 4-й фигуре средний термин занимает место предиката в большей и субъекта в меньшей посылке.
Пример:
Ни один счастливый человек(Р) не стремитсяк справедливости (М)
Некоторые стремящиеся к справедливости люди (M) являются юристами (S)
Применение общих положений (аксиом, законов природы, правовых норм) к частным случаям.
Эту задачу решают силлогизмы по первой фигуре (Напр: Все люди - смертны. Все греки - люди. Следовательно, все греки смертны).
Опровержение неправильных дедукций или неправильных подчинений.
Данная задача противоположна 1-й и силлогизмы ее решающие часто используются для опровержения неправильных
выводов, сделанных по 1-й фигуре.
Эту задачу решают силлогизмами по 2-й фигуре (Напр: Этот смерт. удар нанесен человеком огромной силы.
Обвиняемый не является человеком огромной силы. Значит, обвиняемый не нанес этот смертельный удар).
Обоснование исключений из общих положений.
Эта ситуация часто встречается в споре. Предположим, ваш оппонент выдвигает какое-либо общее
положение, а вам надо доказать исключение из него. Тогда можно смело прибегнуть к 3-ей фигуре
(Напр: Предположим, нам надо доказать, что суждение "все люди имеют преступные склонности"
не является истинным. Тогда нам надо построить силлогизм по 3-ей фигуре:
Ни один ребенок не имеет преступных наклонностей. Каждый ребенок является человеком.
Следовательно, некоторые люди не имеют преступных наклонностей)
Модусы - это определенные сочетания видов суждений в фигурах силлогизма.
Всего возможно 256 модусов силлогизмов.
Модусы силлогизмов бывают правильные и неправильные. Правильные соответствуют правильным
умозаключениям, неправильные - неправильным. Правильными являются 24 модуса. Однако
традиционно рассматриваются только 19 модусов
| Фиг. I | Фиг. II | Фиг. III | Фиг. IV |
| AAA (Barbara) | EAE (Cesare) | AAI (Darapti) | AAI (Bramantip) |
| EAE (Celarent) | AEE (Camestres) | IAI (Disamis) | AEE (Camenes) |
| AII (Darii) | EIO (Festino) | AII (Datisi) | IAI (Dimaris) |
| EIO (Ferio) | AOO (Baroco) | EAO (Felapton) | EAO (Fesapo) |
| OAO (Bocardo) | EIO (Fresison) | ||
| EIO (Ferison) |
Символическая запись модусов расшифровывается так: левый символ указывает вид бoльшей посылки,
средний символ - меньшей посылки, а правый - вид заключения.
Ход рассуждения по 4-й фигуре не типичен для процесса мышления (4-я фигура является искусственной) правила этой фигуры нами не рассматриваются
1. Энтимема (сокращенный силлогизм) (от греч. cлов en tyme - в уме) - это умозаключение, в котором опущена одна из посылок или заключение.
В жизни мы опускаем в своих рассуждениях очевидные посылки, неявно их предполагая.
Рассмотрим механизм образования энтимем
Все пороки заслуживают наказания
Курение - порок
С опущенной бoльшей посылкой: "Курение заслуживает наказания, потому что оно порок"
С опущенной меньшей посылкой: "Всякий порок заслуживает наказания, поэтому курение заслуживает наказания:
С опущенным заключением: "Всякий порок заслуживает наказания, а курение - это порок"
Энтимема часто используется в повседневном мышлении и в ораторской практике.
Сокращенная форма способствует лучшему восприятию. Кроме того при помощи энтимемы достигается
эффект убедительности, так как собеседник вынужден реконструировать ее до полного умозаключения и
начинает считать заключение своим собственным.
2. Полисиллогизм (сложный силлогизм) - сочетание двух или более простых силлогизмов, в котором
заключение предшествующего силлогизма (просиллогизма) становистся посылкой последующего
(эписиллогизма).
Различают прогрессивный и регрессивный полисиллогизм.
а) Прогрессивным полисиллогизмом называется полисиллогизм, в котором заключение просиллогизма становится бoльшей посылкой эписиллогизма.
Все живые существа смертны Люди живые существа Просиллогизм
Люди - смертны Люди - смертны Греки - люди Эписиллогизм
Греки - смертны Греки - смертны Сократ - грек Эписиллогизм
Сократ смертен
С помощью этого прогрессивного полисиллогизма мы поэтапно с максимальной очевидностью перенесли признак "смертный" с общего понятия "живое существо" на единичное понятие "Сократ"
б) Регрессивным полисиллогизмом называется полисиллогизм, в котором заключение просиллогизма становится меньшей посылкой эписиллогизма.
Все мыслящие люди способны к самосовершенствованию
Некоторые преступники являются мыслящими людьми
3. Сорит (сокращенный полисиллогизм) (от греч. soros - куча). В такой форме вывода пропущены заключения простых силлогизмов, которые образуют бoльшую или меньшую посылки эписиллогизмов.
Аналогично полисиллогизму сориты бывают прогрессивные (гоклениевские, по имени автора - нем. логика Гоклена (1547-1628)) и регрессивные (аристотелевские)
В прогрессивном сорите пропущены бoльшие посылки эписиллогизмов:
Все живые существа смертны Люди живые существа ------------------ Греки - люди --------------- Сократ - грек
Сократ смертен В регрессивном сорите пропущены меньшие посылки эписиллогизмов: Все силлогизмы - дедуктивные умозаключения Энтимемы - силлогизмы ---------------------------- Дедуктивные умозаключения - рассуждения от общего к частному ------------------------------------------------------
Энтимема - рассуждение от общего к частному
4. Эпихейрема (от греч. Epiheirema - умозаключение) - сложносокращенный силлогизм, в котором обе посылки - энтимемы.
Гепатит лечится в стационаре, т. к. он - инфекц. заболевание -1-я энтимема
У вас - гепатит, т.к. у вас обнаружен вирус гепатита А -2-я энтимема
Данная эпихейрема состоит из двух энтимем с пропущенными бoльшими посылками.
Умозаключения могут состоять не только из простых, но и
из сложных суждений. Мы рассмотрим наиболее употребляемые - условные и разделительные силлогизмы.
1. Условный силлогизм - силлогизм, в котором хотя бы одна посылка
является импликативным (условным) суждением.
| Поненс | Толленс | ||
| p→q | p→q | p→q | p→q |
| p | q | ¬p | ¬q |
| q | p | ¬q | ¬p |
Модус поненс (лат. modus ponens) - утверждающий модус (его заключение утвердительное суждение)
Модус толленс (лат. modus tollens) отрицающий(его заключение отрицательное суждение).
Модус поненс (рассуждение идет
от утверждения основания к утверждению следствия):
| p→q | Если в империях начинает рушиться семья, то они обращаются в прах. |
| p | В Римской империи начала рушиться семья. |
| q | Она обратилась в прах. |
Модус толленс (рассуждение идет от отрицания
следствия к отрицанию основания):
| p→q | Если подготовлюсь, то сдам экзамен. |
| ¬q | Экзамен я не сдал |
| ¬p | Я не подготовился. |
| p→q | Если это - булочка, то это - съедобно |
| ¬p | Это - не булочка |
| ¬q | (вероятно) это - несъедобно |
| p→q | Если это - булочка, то это - съедобно |
| q | Это - съедобно |
| p | (вероятно) это - булочка |
Данные модусы не позволяют установить главную причину
следствия и поэтому дают лишь правдоподобные заключения.
2. Разделительный (альтернативный) силлогизм - силлогизм, в котором есть
исключающе-разделительное суждение(строгая дизъюнкция).
| S есть Р или Р1 | Составляющая атома - либо заряженная, либо нейтральная. |
| Р есть Р2 или РЗ | Заряженная составляющая атома - либо электрон, либо протон. |
| S есть Р1 или Р2 или РЗ | Составляющая атома - либо электрон, либо протон, либо нейтральна. |
б) в разделительно-категорическом силлогизме большая посылка - строго разделительное
суждение, а меньшая - категорическое.
Имеет два модуса:
| pvq | Либо пан, либо пропал. |
| p | Пан. |
| ¬q | Не пропал. |
| pvq | Либо пан, либо пропал. |
| ¬p | Не пан |
| q | Пропал. |
Все эти формы непосредственно следуют из определения импликации и строгой дизъюнкции через таблицы истинности, а правильные формы выражают логические законы.
Кроме того, часто встречаются и условно-разделительные силлогизмы, в которых большая посылка - конъюнкция условных суждений, а меньшая - разделительное суждение. В зависимости от числа членов дизъюнкции (альтернатив) выделяют дилеммы (2 члена), трилеммы (3 члена), полилеммы (более трех членов). Например, логическая структура известной сказочной ситуации "витязя на распутье" (прямо поедешь - голову сложишь, направо поедешь - коня потеряешь, налево поедешь - жену найдешь) имеет форму трилеммы:
| (p1→q1)&(p2→q2)&(p3→q3) |
| p1vp2vp3 |
| q1vq2vq3. |
Индуктивные умозаключения - это умозаключения, в которых из частных посылок делают
общий вывод.
Дедукция, строго говоря, не дает нового знания. Ее задача - обоснование истины. Индукция - расширяет наше знание, т.к. является обобщением, но дает не достоверный, а вероятный вывод.
Исчерпывающее индуктивное обобщение, когда рассматриваемый класс конечен и не слишком велик, так что мы можем исследовать все частные случаи считается полной индукцией.
Полная индукция - умозаключение, в котором на
основе принадлежности признака каждому элементу класса делается вывод о его принадлежности классу
в целом.
Обычно число обобщаемых случаев бесконечно велико и индукция является неполной
Неполная индукция - умозаключение, в котором
на основе принадлежности признака лишь некоторым элементам класса делают вывод о его принадлежности
классу в целом.
| Схема полной индукции: |
| S1 имеет признак P |
| S2 имеет признак P |
| S3 имеет признак P |
| …………… |
| S50 имеет признак Р |
| S1, S2, S3,…, S50 - образуют весь класс S |
| Все S имеют признак Р, |
| Схема неполной индукции: |
| S1 имеет признак P |
| S2 имеет признак P |
| S3 имеет признак P |
| …………… |
| Sn имеет признак Р |
| S1, S2, S3,…, Sn - образуют лишь часть объема S |
| (Вероятно) все S есть Р |
Неполная индукция может быть популярной и научной
Популярная индукция - умозаключение, в котором путем перечисления фактов по случайному признаку заключают о принадлежности этого признака всему классу явлений.
Это приводит к ненадежности выводов, причем неконтролируемой ненадежности, поскольку невозможно оценить меру достоверности (вероятность истинности) вывода.
Научная индукция - умозаключение, в котором обобщение строится путем отбора существенных признаков.
Для научной индукции характерна систематичность и методичность отбора данных для обобщения выраженных в наборе суждений, обосновывающих вывод, стремление использовать в конкретных обобщениях знание сущностных свойств и закономерностей предметной области, законов статистики. Так, к научной индукции можно отнести многообразные статистические методы, широко используемые в науке и практике.
Умозаключение по аналогии - умозаключение, в котором на основании сходства одних признаков
предмета делается вывод о сходстве других признаков.
| А имеет признаки a, b, c, d. |
| В имеет признаки a, b, c. |
| Вероятно, В имеет признак d. |
| где a, b, c - общие признаки, d - переносимый (экстраполируемый). |
В основе рассуждения по аналогии лежит сходство между предметами. Степень достоверности такого вывода зависит как от числа сходных признаков (чем больше, тем лучше), так и от их существенности (чем существеннее признак, тем вероятнее правильный вывод).

