Часть вторая

Теоретические основы построения чертежа

Глава 10. Позиционные задачи

§ 66. Построение линии пересечения поверхностей способом вспомогательных сфер

При построении линии пересечения поверхностей особенности пересечения соосных поверхностей вращения позволяют в качестве вспомогательных поверхностей-посредников использовать сферы, соосные с данными поверхностями.

К соосным поверхностям вращения относятся поверхности, имеющие общую ось вращения. На рис. 134 изображены соосные цилиндр и сфера (рис. 134, а), соосные конус и сфера (рис. 134, 6) и соосные цилиндр и конус (рис. 134, в).

Рис. 134

Соосные поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения. Этих общих для обеих поверхностей окружностей столько, сколько существует точек пересечения очерковых линий поверхностей. Поверхности на рис. 134 пересекаются по окружностям, создаваемым точками 7 и 2 пересечения их главных меридианов.

Вспомогательная сфера-посредник пересекает каждую из заданных поверхностей по окружности, в пересечении которых получаются точки, принадлежащие и другой поверхности, а значит, и линии пересечения.

Если оси поверхностей пересекаются, то вспомогательные сферы проводят из одного центра-точки пересечения осей. Линию пересечения поверхностей в этом случае строят способом вспомогательных концентрических сфер.

При построении линии пересечения поверхностей для использования способа вспомогательных концентрических сфер необходимо выполнение следующих условий:

1. пересечение поверхностей вращения;
2. оси поверхностей - пересекающиеся прямые - параллельны одной из плоскостей проекций, т. е. имеется общая плоскость симметрии;
3. нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях.

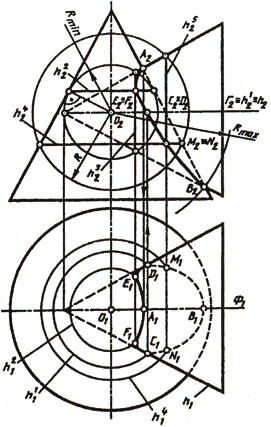
Обычно способ вспомогательных сфер используется в сочетании со способом вспомогательных секущих плоскостей. На рис. 135 построена линия пересечения двух конических поверхностей вращения с пересекающимися во фронтальной плоскости уровня Ф(Ф₁) осями вращения.

Рис. 135

Значит, главные меридианы этих поверхностей пересекаются и дают в своем пересечении точки видимости линии пересечения относительно плоскости П₂ или самую высокую А и самую низкую В точки. В пересечении горизонтального меридиана h и параллели h¹, лежащих в одной вспомогательной секущей плоскости Г(Г₂), определены точки видимости С и D линии пересечения относительно плоскости П₁. Использовать вспомогательные секущие плоскости для построения дополнительных точек линии пересечения нецелесообразно, так как плоскости, параллельные Ф, будут пересекать обе поверхности по гиперболам, а плоскости, параллельные Г, будут давать в пересечении поверхностей окружности и гиперболы. Вспомогательные горизонтально или фронтально проецирующие плоскости, проведенные через вершину одной из поверхностей, будут пересекать их по образующим и эллипсам.

В данном примере выполнены условия, позволяющие применение вспомогательных сфер для построения точек линии пересечения. Оси поверхностей вращения пересекаются в точке 0(0₁; О₂), которая является центром вспомогательных сфер, радиус сферы изменяется в пределах R_min < R < R_max. Радиус максимальной сферы определяется расстоянием от центра О наиболее удаленной точки В (R_max = 0₂B₂), а радиус минимальной сферы определяется как радиус сферы, касающейся одной поверхности (по окружности h²) и пересекающей другую (по окружности h³).

Плоскости этих окружностей перпендикулярны осям вращения поверхностей. В пересечении этих окружностей получаем точки Е и F, принадлежащие линии пересечения поверхностей:

h₂² ∩ h₂³ = E₂(F₂); E₂E₁ ׀׀ A₂A₁; E₂E₁ ∩ h₁² = E₁; F₂F₁ ∩ h₁² = F₁.

Промежуточная сфера радиуса R пересекает поверхности по окружностям h⁴ и h⁵, в пересечении которых находятся точки М и N:

h₂⁴ ∩ h₂⁵ = M₂(N₂); M₂M₁ ׀׀ A₂A₁; M₂M₁ ∩ h₁⁴ = M₁; N₂N₁ ∩ h₁⁴ = N₁

Соединяя одноименные проекции построенных точек с учетом их видимости, получаем проекции линии пересечения поверхностей.

Инженерная графика

© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения