Часть вторая |
Теоретические основы построения чертежа |
 |
Глава 11. Метрические задачи |
|
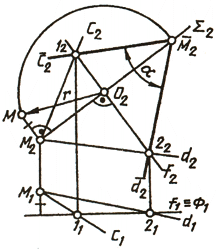
§ 70. Определение истинной величины угловЗадачу на определение истинной величины углов (плоских) удобнее решать путем преобразования исходного чертежа способом вращения вокруг линии уровня. Истинная величина углов между пересекающимися прямыми c и d (рис. 143) определена следующим образом: плоскость угла повернута вокруг своей фронтали f(1, 2) до совмещения ее с фронтальной плоскостью уровня Ф(Ф1), проходящей через фронталь f. Проекция М2 совмещения вершины М угла между прямыми с и d находится на проекции Σ2 фронтально проецирующей плоскости Σ, в которой вращается точка М. Определив с помощью прямоугольного треугольника О2М2М натуральную величину радиуса вращения r и отложив ее на проекции Σ2 от фронтальной проекции центра вращения, получаем изображение точки М на плоскости П2 в совмещенном с плоскостью Ф положении. Соединяя фронтальные проекции неподвижных точек 1 и 2 с построенной точкой М, получаем проекции с2 и d2, совмещенных с плоскостью Ф прямых с и d. Угол между прямыми с2 и d2 определяет натуральную величину искомого угла между пересекающимися прямыми c и d.
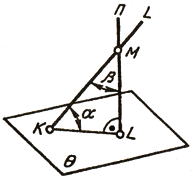
Рис. 143 Эта задача также может быть решена способом замены плоскостей проекции. Для этого двойной заменой плоскостей проекций нужно сделать плоскость угла плоскостью уровня, решив последовательно сначала третью исходную задачу, а затем - четвертую. Натуральная величина угла между скрещивающимися прямыми определяется как угол между двумя пересекающимися прямыми, параллельными данным скрещивающимся прямым. Угол α между прямой l и плоскостью Θ может быть определен через дополнительный угол β между заданной прямой l и перпендикуляром n к данной плоскости, проведенной из любой точки прямой (рис. 144).
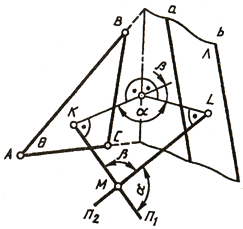
Рис. 144 Угол β дополняет искомый угол α до 90°. Определив истинную величину угла β путем вращения вокруг прямой уровня плоскости угла, образованного прямой l и перпендикуляром n, остается дополнить его до прямого угла. Этот дополнительный угол и даст истинную величину угла α между прямой l и плоскостью Θ. Истинная величина двугранного угла - угла между двумя плоскостями Θ и λ — может быть определена или путем замены плоскости проекций с целью преобразования ребра двугранного угла в проецирующую прямую (задачи 1 и 2), или, если ребро не задано, как угол между двумя перпендикулярами n1 и n2, проведенными к данным плоскостям (см. § 61) из произвольной точки М пространства (рис. 145).
Рис. 145 В плоскости этих перпендикуляров при точке М получаем два плоских угла α и β, которые соответственно равны линейным углам двух смежных углов (двугранных), образованных плоскостями Θ и λ. Определив истинную величину углов между перпендикулярными n1 и n2 путем вращения вокруг прямой уровня, тем самым определим и линейный угол двугранного угла, образованного плоскостями Θ и λ. |
||
Инженерная графика |
||
© Красноярский государственный аграрный университет |